Содержание
- 2. Логические представления – описание системы, процесса или явления в виде совокупности сложных высказываний, составленных из простых
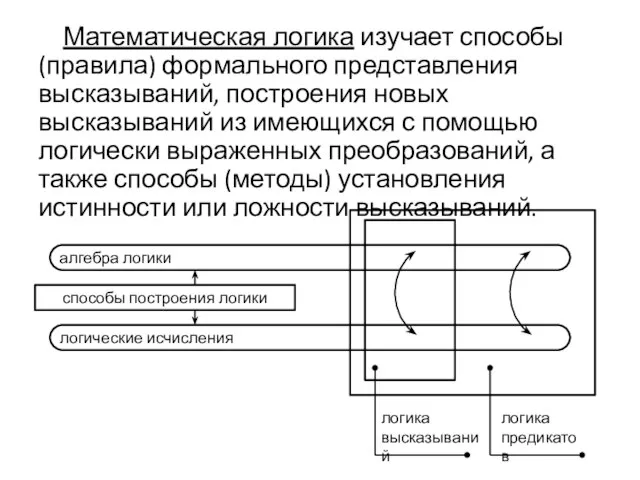
- 3. Математическая логика изучает способы (правила) формального представления высказываний, построения новых высказываний из имеющихся с помощью логически
- 4. Основными объектами разделов логики являются высказывания. Высказывание – последовательное предложение (утверждение, суждение), о котором можно говорить,
- 5. 4.1. Основные понятия. Простое (элементарное) высказывание – рассматривается как неделимое целое. Обычно это высказывания не содержащие
- 6. Основные логические связки (операции) логики высказываний: Конъюнкция (операция «И», логическое произведение) - P&Q, P∧Q, P∙Q -
- 7. Отрицание (инверсия) - P, P - «не P», «неверно, что P» Импликация (логическое следование) - P→Q,
- 8. Неравнозначность (исключающее «ИЛИ») - P⊕Q, P∆Q - «либо P, либо Q», «или P, или Q» -
- 9. Пример 1. Представить логическими формулами следующие высказывания: Сегодня понедельник или вторник. Идёт дождь или снег. Если
- 10. Пример 2. Записать логическими формулами следующие высказывания: Если допоздна работаешь с компьютером и при этом пьёшь
- 12. Скачать презентацию








 Научно-Инновационное предприятие СКГМИ (ГТУ) "Стройкомплект-Инновации"
Научно-Инновационное предприятие СКГМИ (ГТУ) "Стройкомплект-Инновации" Скандинавский стиль
Скандинавский стиль WEB- браузеры
WEB- браузеры Биологическая безопасность и современные подходы к обеззараживанию воздуха в помещениях ЛПУ
Биологическая безопасность и современные подходы к обеззараживанию воздуха в помещениях ЛПУ Эволюционно-генетические аспекты иммунологии репродукции
Эволюционно-генетические аспекты иммунологии репродукции Подготовка к ЕГЭ Задания В1-В3 Вариант 3
Подготовка к ЕГЭ Задания В1-В3 Вариант 3 Строение тела человека
Строение тела человека Парейдолии в еде
Парейдолии в еде 1 Об итогах социально- экономического развития Сивинского муниципального района в сфере РЧП ФЦБ «РАЗВИТИЕ ЧЕЛОВЕЧЕСКОГО ПОТЕНЦИА
1 Об итогах социально- экономического развития Сивинского муниципального района в сфере РЧП ФЦБ «РАЗВИТИЕ ЧЕЛОВЕЧЕСКОГО ПОТЕНЦИА Презентация на тему Чехов "Злоумышленник" 7 класс
Презентация на тему Чехов "Злоумышленник" 7 класс Гибкие печатные платы
Гибкие печатные платы Экологические проблемы водоёмов
Экологические проблемы водоёмов Филиал ООО компания Тензор. Сфера торгов
Филиал ООО компания Тензор. Сфера торгов Сравнительная характеристика кредитных расчетов банков города Красноярска
Сравнительная характеристика кредитных расчетов банков города Красноярска ХИРУРГИЧЕСКАЯ АНАТОМИЯ КРУПНЫХ СУСТАВОВ КОНЕЧНОСТЕЙ
ХИРУРГИЧЕСКАЯ АНАТОМИЯ КРУПНЫХ СУСТАВОВ КОНЕЧНОСТЕЙ Питер Брейгель. Фламандские пословицы
Питер Брейгель. Фламандские пословицы Федеральный государственный образовательный стандарт дошкольного образования
Федеральный государственный образовательный стандарт дошкольного образования Презентация на тему Бангладеш
Презентация на тему Бангладеш  ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ
ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ Презентация на тему Здоров будешь - все добудешь
Презентация на тему Здоров будешь - все добудешь Фракталы вокруг нас
Фракталы вокруг нас Презентация на тему Ораторская речь,её особенности
Презентация на тему Ораторская речь,её особенности school
school Семейка самоцветов
Семейка самоцветов Йомаклы әлифба
Йомаклы әлифба Инвестиционные проекты, Казахстан
Инвестиционные проекты, Казахстан Органы дыхания и газообмен 7 класс
Органы дыхания и газообмен 7 класс Презентация на тему Новогодний сувенир в технике кистевой росписи
Презентация на тему Новогодний сувенир в технике кистевой росписи