Макроэкономика

Вопросы
Равновесие на товарных рынках, кривая IS
Равновесие на денежном рынке, кривая LM
Совместное равновесие на товарных и денежном рынках в модели IS-LM
Модель IS-LM в краткосрочном и долгосрочном периодах. Модель IS-LM с гибкими ценами. Соотношение моделей IS-LM и AD-AS

Недостатки кейнсианской модели
Кейнсианская макроэкономическая модель («доходов и
расходов») в интерпретации кейнсианского креста
полезна, так как показывает, что определяет доход в
экономике при определенном уровне планируемых
инвестиций. Однако она является чрезмерным
упрощением, так как
уровень планируемых инвестиций фиксирован
экономика попадает в ситуацию либо инфляции, либо безработицы
в модели нет уровня цен, все измеряется реальными показателями, при этом обсуждаются проблемы инфляции

Модель IS-LМ как преодоление противоречий модели кейнсианского креста
Анализ ведется в двух секторах экономики:
в реальном, в котором условием равновесия является I=S
в денежном, где условием равновесия является равенство спроса на ликвидность и денежной массы L=M
Цель построения модели – определение условий
совместного равновесия на двух рынках – товарном и
денежном

Равновесие на товарных рынках. Кривая IS
Ограничения и допущения
Закрытая экономика
Неизменные параметры бюджетно-налоговой политики (государственные расходы и налоги не меняются)
Анализ такой же, как и в модели кейнсианского креста
Потребительская функция и сбережения зависят от дохода C=C(Y) S=S(Y) S’(Y)>0
Равенство между сбережениями и инвестициями обеспечивает равновесие на товарных рынках S(Y)=I(r )
Но, наряду с потребительской, вводится инвестиционная функция
Решения об инвестициях принимают в зависимости от высоты процентной ставки I=I(r) I’(r )<0

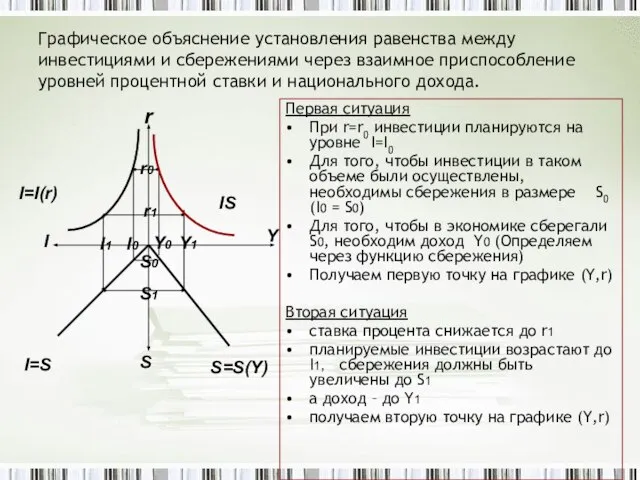
Графическое объяснение установления равенства между инвестициями и сбережениями через взаимное приспособление уровней процентной ставки и национального дохода.
Первая ситуация
При r=r0 инвестиции планируются на уровне I=I0
Для того, чтобы инвестиции в таком объеме были осуществлены, необходимы сбережения в размере S0 (I0 = S0)
Для того, чтобы в экономике сберегали S0, необходим доход Y0 (Определяем через функцию сбережения)
Получаем первую точку на графике (Y,r)
Вторая ситуация
ставка процента снижается до r1
планируемые инвестиции возрастают до I1, сбережения должны быть увеличены до S1
а доход – до Y1
получаем вторую точку на графике (Y,r)
r
I
S
Y
r0
r1
I1 I0
I=S
I=I(r)
S=S(Y)
S1
S0
Y0 Y1
IS

Выводы
Каждой процентной ставке соответствует
определенный уровень национального дохода
Соединив все точки на графике (Y,r), получаем кривую
IS, каждая точка на которой дает нам такую
комбинацию процентной ставки и дохода, при
которых на товарных рынках установится
равновесие
Кривая IS показывает, что, чем выше процентная
ставка, тем ниже уровень планируемых инвестиций и,
следовательно, ниже уровень дохода

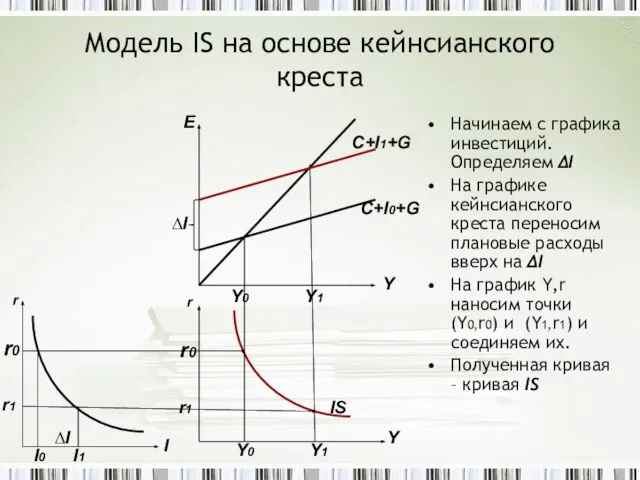
Модель IS на основе кейнсианского креста
Начинаем с графика инвестиций. Определяем ∆I
На графике кейнсианского креста переносим плановые расходы вверх на ∆I
На график Y,r наносим точки (Y0,r0) и (Y1,r1) и соединяем их.
Полученная кривая – кривая IS
r
r0
r0
r1
r1
I0 I1
∆I
∆I
r
Y
Y
E
I
Y0 Y1
Y0 Y1
C+I0+G
C+I1+G
IS

Алгебраическое построение кривой IS (1)
Экономика закрытая, функции потребления и инвестиций линейны
Тогда Y= C(Y-T)+I(r)+G
Пусть функция потребления представлена как
C=a+b(Y-T),
где a и b – положительные параметры
а- автономное потребление, b – предельная склонность к потреблению
Инвестиционная функция представлена в виде
I=c-dr,
где c и d – положительные параметры
c – автономные инвестиции
d – параметр, определяющий, каким образом инвестиции реагируют на ставку процента. Чем больше этот коэффициент, тем чувствительнее инвестиции к процентной ставке, и наоборот. Так как инвестиции при увеличении процентной ставки падают, перед d стоит знак “-“

Алгебраическое построение кривой IS (2)
Подставим уравнения потребления и инвестиций в
тождество национальных счетов и преобразуем его
Y=[a+b(Y-T)]+(c-dr)+G
Y-bY=a-bT+c-dr+G
Y(1-b)= (a+c)+(G-bT)-dr
Y= (a+c)/(1-b) + 1/(1-b)G – b/(1-b)T – d/(1-b)r
Это уравнение выражает кривую IS алгебраически. Оно дает параметры уровня дохода Y при любой ставке процента r и переменных бюджетно-налоговой политики G и T
При неизменных G и T оно показывает связь между Y и r

Экономический смысл коэффициентов
1/(1-b) – мультипликатор расходов
– b/(1-b) – налоговый мультипликатор
d/(1-b) – коэффициент, показывающий чувствительность Y к изменениям r и определяет крутизну IS
Чем больше d, тем чувствительнее к изменением процентной ставки
инвестиции, а, следовательно, и доход. Небольшое изменение
процентной ставки приводит к большим изменениям в доходе – кривая IS –
пологая. И наоборот
Чем больше склонность к потреблению, тем больше мультипликатор.
Значит, даже небольшие изменения в инвестициях, вызванные
изменениями процентной ставки, приведут к существенным изменениям в
доходе кривая IS – пологая. И наоборот
Знак «-» перед коэффициентом d/(1-b) говорит о том, что кривая IS имеет
отрицательный наклон

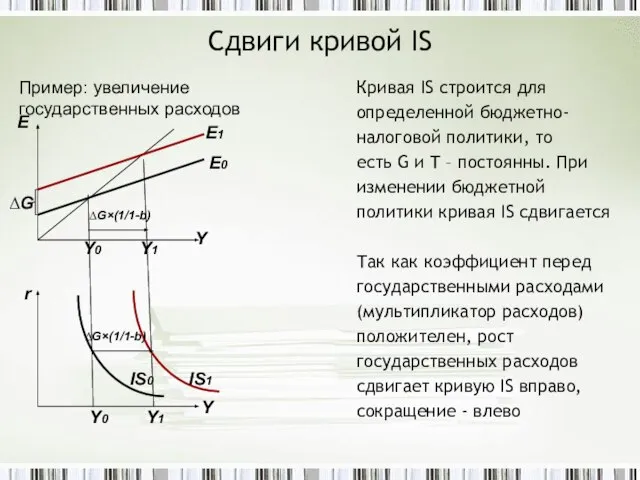
Сдвиги кривой IS
Кривая IS строится для
определенной бюджетно-
налоговой политики, то
есть G и T – постоянны. При
изменении бюджетной
политики кривая IS сдвигается
Так как коэффициент перед
государственными расходами
(мультипликатор расходов)
положителен, рост
государственных расходов
сдвигает кривую IS вправо,
сокращение - влево
Пример: увеличение
государственных расходов
E
Y
Y
r
Y0 Y1
Y0 Y1
∆G×(1/1-b)
∆G×(1/1-b)
∆G
E0
E1
IS0
IS1

Сдвиги кривой IS
Поскольку коэффициент
при налогах (налоговый
мультипликатор)
отрицателен, рост
налогов сдвигает кривую
IS влево, а уменьшение –
вправо
Пример: увеличение налогов
E
Y
Y
r
Y1 Y0
Y1 Y0
∆T×(-b/1-b)
-∆С
E1
E0
IS1
IS0
∆T×(-b/1-b)

Кривая LM
Ограничения и
допущения
Предложение денег постоянно
Цены не меняются
Спрос на деньги состоит из трансакционного спроса и спроса на деньги как имущество
r
Y
M/P
Lим.=L(r)
LM
M/P
Lим.0 Lим.1
Lсд.0
Lсд.1
L=L(Y)
r1
ro
Y0 Y1

Построение кривой LM
Начинаем со второго квадранта
Доход Yo вызывает потребность в деньгах для обеспечения сделок
Lcд.0
Оставшаяся часть денег должна быть поглощена спекулятивным спросом (спросом на деньги как имущество) Lим.o
На графике в квадранте 4 определяем процентную ставку ro , при которой население и фирмы добровольно держали бы оставшиеся деньги.
На графике в первом квадранте получаем точку, соответствующую паре Y 0 и r0
Повторим все то же для нового уровня дохода (больше доход
⇒больше денег для сделок⇒меньше денег как имущества⇒население
и фирмы добровольно откажутся от хранения денег только, если ставка
процента возрастет⇒ставка растет)
Получаем новую пару значений Y1, r1 и соединяем точки на графике
Это кривая LM, каждая точка на которой показывает такую
комбинацию дохода и процентной ставки, при которых на
денежном рынке устанавливается равновесие

Алгебраическое построение кривой LM
При равновесии на денежном рынке спрос на деньги
равен их предложению
M/P=L(Y,r)
Пусть функция спроса на деньги линейна
L(Y,r)=eY – fr
где e и f - положительны
e –показывает, насколько возрастает спрос на деньги с ростом дохода
f – определяет, на сколько падает спрос на деньги при росте ставки процента
Знак «-» перед процентом говорит об обратной связи между процентной ставкой и спросом на деньги

Алгебраическое построение кривой LM
Запишем условие равновесия на денежном рынке
M/P = eY – fr
Преобразуем его так, чтобы процентная ставка
оказалась слева
r = (e/f)Y – (1/f) (M/P)
Это уравнение дает нам величину ставки процента,
которая обеспечивает равновесие денежного рынка
при любом значении дохода и реального предложения
денег. Кривая LM графически отражает это уравнение
для разных значений Y и r при фиксированных
значениях M/P

Значение коэффициентов
Поскольку коэффициент при Y положителен, то кривая LM имеет положительный наклон: более высокий доход требует более высокой ставки процента для обеспечения равновесия на денежном рынке
Так как коэффициент при реальных запасах денежных средств (M/P) отрицателен, их уменьшение сдвигает кривую LM вверх, а увеличение – вниз
коэффициент e/f определяет наклон кривой. Если значение “е” невелико, т.е. спрос на деньги мало чувствителен к изменениям дохода, то кривая LM – полога (требуется небольшое изменение в ставках процента, чтобы компенсировать незначительный рост трансакционного спроса на деньги)
если f мало (т.е. спрос на деньги слабо зависит от ставки процента), то кривая LM - крутая, так как сдвиг спроса на деньги вследствие изменения дохода ведет к значительному изменению процента

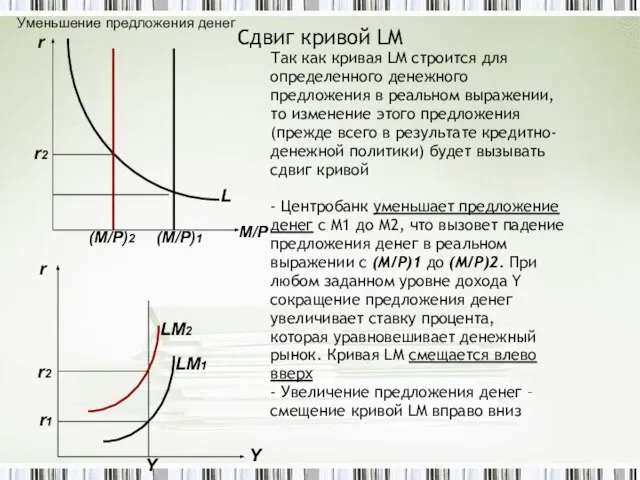
Сдвиг кривой LM
Так как кривая LM строится для
определенного денежного
предложения в реальном выражении,
то изменение этого предложения
(прежде всего в результате кредитно-
денежной политики) будет вызывать
сдвиг кривой
- Центробанк уменьшает предложение
денег с М1 до М2, что вызовет падение
предложения денег в реальном
выражении с (M/P)1 до (M/P)2. При
любом заданном уровне дохода Y
сокращение предложения денег
увеличивает ставку процента,
которая уравновешивает денежный
рынок. Кривая LM смещается влево
вверх
- Увеличение предложения денег –
смещение кривой LM вправо вниз
r
r
M/P
(M/P)2 (M/P)1
r2
r1
r2
L
Y
Y
Уменьшение предложения денег
LM1
LM2

Трактовка кривой LM с точки зрения количественной теории денег
Согласно количественной теории MV=PY
При этом скорость обращения денег V предполагается
постоянной
Это означает, что для любого уровня цен только
предложение денег определяет уровень дохода. Иначе
говоря, уровень дохода не зависит от ставки процента
и кривая LM должна быть вертикальной
r LM
Y

Трактовка кривой LM с точки зрения количественной теории денег
Нормальную кривую LM с положительным наклоном можно
получить из количественной теории денег, только сняв
предпосылку о постоянной скорости обращения денег
В реальности спрос на деньги зависит и от ставки процента: более
высокая ставка процента увеличивает издержки владения
деньгами и уменьшает спрос на деньги
Поскольку люди реагируют на более высокую процентную ставку
уменьшением запасов денег, каждая денежная единица в
экономике переходит из рук в руки быстрее, т.е. увеличивается
скорость обращения денег
Можно, поэтому, записать
MV(r)=PY
V=V(r) V’(r)>0, то есть скорость обращения положительно
связана со ставкой процента

MV(r)=PY
Такое уравнение количественной теории денег дает кривую LM с положительным наклоном. Поскольку рост процентной ставки увеличивает скорость обращения, он увеличивает Y при заданных M и P
При заданных r и P рост M ведет к росту Y. Кривая LM сдвигается вправо
Уменьшение M приводит к сдвигу кривой LM влево
Таким образом, количественная теория денег дает ту же кривую LM, что и теория предпочтения ликвидности, только в другой трактовке

Совместное равновесие на товарных и денежном рынках в модели IS-LM
Модель IS-LM используется для объяснения
функционирования экономики в краткосрочном
периоде, когда уровень цен фиксирован.
Модель состоит из двух уравнений
Y= C(Y-T)+I(r)+G IS
M/P=L(r,Y) LM
бюджетно-налоговая политика G и Т
кредитно-денежная политика М экзогенные
уровень цен Р переменные

Совместное равновесие на товарных и денежных рынках
При заданных G, T, М и Р кривая IS дает такие комбинации дохода
и процентной ставки, которые обеспечивают равновесие на рынке
товаров и услуг, а кривая LM – такие комбинации r и Y, которые
удовлетворяют равновесию на денежном рынке
r
Экономическое равновесие в модели IS-LM – это точка
пересечения, которая одновременно удовлетворяет условиям
равновесия как на товарных, так и на денежном рынках
(в точке пересечения двух кривых реальные
расходы равны планируемым, а спрос на реальные денежные
средства равен предложению денег)
LM
IS
Y
Y*
r*

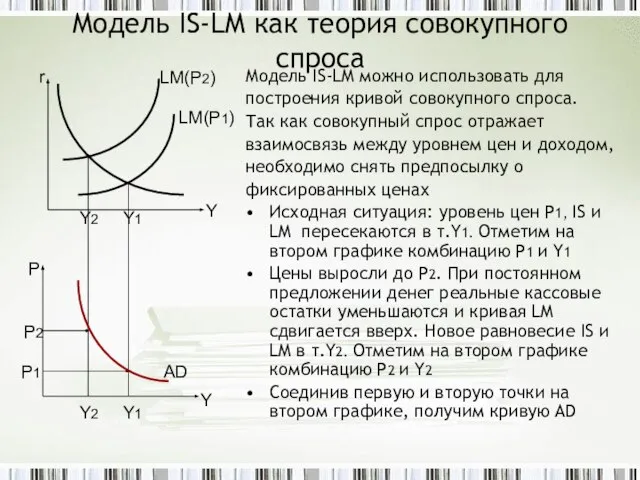
Модель IS-LM как теория совокупного спроса
Модель IS-LM можно использовать для
построения кривой совокупного спроса.
Так как совокупный спрос отражает
взаимосвязь между уровнем цен и доходом,
необходимо снять предпосылку о
фиксированных ценах
Исходная ситуация: уровень цен Р1, IS и LM пересекаются в т.Y1. Отметим на втором графике комбинацию Р1 и Y1
Цены выросли до Р2. При постоянном предложении денег реальные кассовые остатки уменьшаются и кривая LM сдвигается вверх. Новое равновесие IS и LM в т.Y2. Отметим на втором графике комбинацию Р2 и Y2
Соединив первую и вторую точки на втором графике, получим кривую AD
r
LM(P1)
LM(P2)
Y2 Y1
Y2 Y1
Y
Y
P
P2
P1
AD

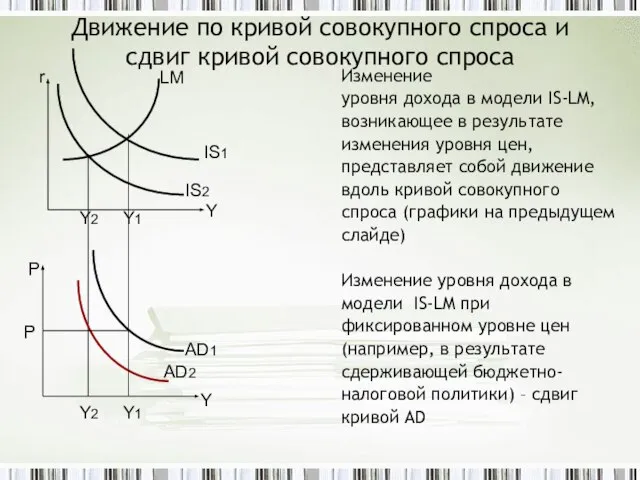
Движение по кривой совокупного спроса и сдвиг кривой совокупного спроса
Изменение
уровня дохода в модели IS-LM,
возникающее в результате
изменения уровня цен,
представляет собой движение
вдоль кривой совокупного
спроса (графики на предыдущем
слайде)
Изменение уровня дохода в
модели IS-LM при
фиксированном уровне цен
(например, в результате
сдерживающей бюджетно-
налоговой политики) – сдвиг
кривой AD
r
LM
Y2 Y1
Y2 Y1
Y
Y
P
P
AD2
IS1
IS2
AD1

Литература
Агапова Т.А., Серегина С.Ф. Макроэкономика. Гл. 9.
Гальперин В.М., Гребенников П.И. и др. Макроэкономика. Гл.3, 4, 6.
Мэнкью Н.Г. Макроэкономика. Гл.9, 10.
Сакс Дж.Д, Ларрен Ф.Б. Макроэкономика. Глобальный подход. Гл. 12.
Лившиц А.Я. Введение в рыночную экономику. М. 1991.

Спасибо за внимание
М-21 Ашыров Максат