Математические игры и головоломки

Содержание
Цели
Математические игры
Головоломки
Выводы
Список литературы

Математические игры
Цели
Из истории
Рэндзю
Ним
Игра Луитуэйта
Заключение
назад

Ним
Описание
Стратегия
Разновидности Нима
назад

Разновидности Нима
Мура
Кегли
Звёздный Ним
назад

Звёздный Ним
Описание
Стратегия
назад

Игра Луитуэйта
Описание
Стратегия
назад

Головоломки
Виды головоломок
Кубик-Рубик
Пятнашки
Заключение
назад

Кубик-Рубик
Формулы операций
Алгоритм сбора
назад

Пятнашки
История
Секрет
назад

Цель
Узнать новые математические игры и головоломки.
Узнать их историю и секреты.
назад

Цели
Математические игры и головоломки очень популярны, как, впрочем, и все игры. И далеко не всегда более сложная игра – более интересная. Часто миллионы людей с неугасаемым интересом играют в самые простые игры, и именно эти игры больше всего ценят, именно они входят в историю математики и прославляют своих создателей.
Наиболее приближенными к математике являются головоломки, но много головоломок образовалось из когда-то существовавших (а некоторые из ещё существующих) игр. Большинство таких основополагающих игр было придумано древнегреческими математиками.
В последнее время математическим играм внимание уделяется, в основном, для нахождения выигрышных стратегий, на что сильно повлияло распространение программирования: составить алгоритм, по которому в игру смог бы играть компьютер, часто бывает сложнее и интереснее, нежели самому научиться играть в неё, при этом глубже вникаешь в суть игры, после чего выиграть в неё можешь уже практически любого.
назад

Из истории
Простейшие математические игры часто используют как задачи, в которых нужно найти выигрышную стратегию, либо одно положение перевести в другое. Иногда задачи бывают весьма простыми, когда они решаются известными методами, такими как инвариант и раскраска, но есть и весьма простые, но до сих пор неразрешённые задачи, связанные с математическими играми.
назад

Рэндзю
Примером может являться популярная игра крестики-нолики на бесконечном поле (рэндзю). Она, как известно, при правильной стратегии обоих игроков бесконечна, но выигрышную стратегию при этом никто не знает. В настоящее время придумано множество алгоритмов этой игры, основанных, прежде всего, на переборе различных вариантов и анализе игры на следующие несколько ходов, которые очень близки к выигрышной стратегии, но лишь при их реализации на компьютере – человек же им следовать практически не может. Существуют простейшие приёмы этой игры, которыми пользуются игроки, но решающей чаще всего бывает внимательность.
назад

Ним
Существует несколько игр, в которых двое играющих A и B, руководствуясь определёнными правилами, по очереди вынимают то или иное число фишек из одной или нескольких кучек – побеждает тот, кто берёт последнюю фишку. Простейшая такая игра – это игра с одной кучкой фишек, и сделать ход в ней – значит взять из кучки любое число фишек от 1 до m включительно. Многие подобные игры поддаются исследованию с помощью числа Шпрага-Гранди G(C). Пустой позиции O, не содержащей фишек, отвечает G(O)=0.
назад

Стратегия
Если G(C)>0, то игрок, делающий следующий ход, допустим, это игрок A, может обеспечить себе выигрыш, если ему удастся перейти к “безопасной” комбинации S с G(S)=0. Действительно, по определению G(S) в этом случае либо S – пустая позиция, и тогда A уже выиграл, либо B следующим ходом должен перейти к “опасной” позиции U с G(U)>0 – и тогда всё повторяется снова. Такая игра после конечного числа ходов заканчивается победой A.
Комбинацию кучек, состоящих соответственно из x, y, … фишек, обозначим C=(x, y, …) и предположим, что допустимые ходы переводят C в другие комбинации: D, E, … Тогда G(C) есть наименьшее неотрицательное число, отличное от G(D), G(E), … Это позволяет по индукции определить G(C) для любой комбинации C, разрешённой правилами игры. Так, в упомянутой задаче G(x)=x mod (m+1).
назад

Мура
Более общий случай представляет игра Мура, которую также можно назвать k-ним. Правила её те же, что и в обычном ниме (1-ним), но здесь разрешается бать фишки из любого количества кучек, не превосходящего k.
назад

Кегли
Ещё одна подобная игра – Кегли. В ней фишки разложены в ряд, и при каждом ходе убирается одна какая-либо фишка или две соседние. При этом ряд может разбиться на два меньших ряда. Выигрывает тот, кто возьмёт последнюю фишку. Обобщённая вариация этой игры известна под именем игры Витхоффа.
назад

Звёздный Ним
Есть интересная вариация игры ним под названием “звёздный ним”. Она довольно проста, но стратегия в ней видна не сразу. Играют в эту игру на звездообразной фигуре, изображённой на рис. 1, слева. Поставьте по одной фишке на каждую из девяти вершин звезды. Игроки A и B делают ходы по очереди, снимая при каждом ходе либо одну, либо две фишки, соединённые отрезком прямой. Тот, кто снимает последнюю фишку выигрывает.
далее далее назад

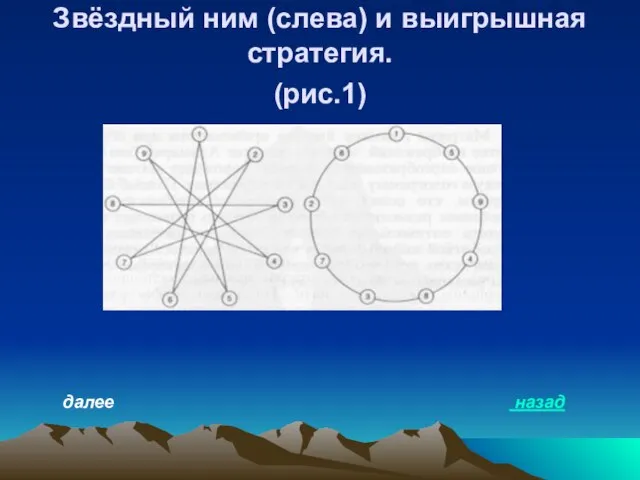
Звёздный ним (слева) и выигрышная стратегия.
(рис.1)
далее назад

У игрока B при игре в звёздный ним есть выигрышная стратегия, использующая симметрию игровой доски (вообще, выигрышные стратегии многих математических игр строятся на этом). Представим, что отрезки прямых, соединяющие вершины звезды, - это нити. Тогда всю конфигурацию можно развернуть в окружность, топологически эквивалентную нитяной звезде. Если A снимает с окружности одну фишку, то B снимает две фишки с противоположного участка окружности. Если A берёт две фишки, то B снимает с противоположного участка окружности одну фишку. В обоих случаях на окружности остаются две группы из трёх фишек. Какую бы фишку (или какие бы фишки) ни взял A из одной группы, B берёт соответствующую фишку (или фишки) из другой группы. Ясно, что последняя фишка достанется игроку B.
назад

Игра Дж. Луитуэйта
В конце 60-х годов Дж. Леутуэйт из шотландского города Терсо изобрёл замечательную игру с искусно скрытой стратегией “парных ходов”, обеспечивающей второму игроку заведомый выигрыш. На доске размером 5*5 квадратных клеток в шахматном порядке расставлены 13 чёрных и 12 белых фишек, после чего любая из чёрных фишек, например, стоящая на центральном поле, снимается.
далее назад

Игра Дж. Луитуэйта (слева) и стратегия парных ходов для неё (справа).
Игрок A ходит белыми фишками, игрок B – чёрными. Ходы делаются по вертикали и горизонтали. Проигравшим считается тот из игроков, кто первым не сможет сделать очередной ход. Если доску раскрасить подобно шахматной доске, то станет ясно, что каждая фишка со своего поля переходит на поле другого цвета и что ни одну фишку нельзя заставить ходить дважды.
далее далее назад

Следовательно, игра для каждого игрока не может продолжаться более 12 ходов. Но она может окончиться и раньше выигрышем для любого игрока, если только B не будет придерживаться рациональной стратегии.
Рациональная стратегия для игрока В состоит в том, чтобы мысленно представить себе всю матрицу (за исключением пустой клетки), покрытую двенадцатью неперекрывающимися костями домино. Как именно они разложены на доске, не имеет значения. На рис. 2, справа показан один из способов покрытия доски костями домино. Какой бы ход ни сделал игрок А, В просто делает ход на ту кость домино, которую только что покинул А. При такой стратегии у В всегда есть ход после очередного хода А, поэтому В заведомо выигрывает за 12 или за меньшее число ходов.
далее далее назад

В игру Леутуэйта можно играть не только фишками на доске, но и квадратными плитками или кубиками, передвигаемыми внутри плоской коробочки, на дне которой начерчена матрица. Предположим теперь, что в правила игры внесена поправка, позволяющая любому игроку в любое время ходить любым числом (от 1 до 4) фишек, стоящих на одной горизонтали или вертикали, если первая и последняя фишки в выбранной им горизонтали или вертикали “его” цвета. Перед нами великолепный пример того, как тривиальное (на первый взгляд) изменение правила приводит к резкому усложнению анализа игры. Леутуэйту не удалось найти выигрышную стратегию ни для одного из игроков в этом варианте игры.
назад

Заключение
Большинство игр, рассмотренных нами, имели выигрышную стратегию, но это не значит, что практически у всех подобных игр она существует. Есть множество игр, выигрышную стратегию в которых на сегодняшний день ещё не изобрели, а есть много и таких, у которых таковой вообще нет.
назад

Головоломки.
Математические головоломки бывают самые разные: вращательные (кубик Рубика), “Волшебные кольца”, “Игры с дыркой” (пятнашки), решётчатые и многие другие. Мы рассмотрим лишь некоторые из них.
назад

Кубик-Рубик
Вращательными называются головоломки, суть которых заключается в поворотах рядов кубиков (и не только кубиков), из которых они состоят.
Знаменитейшая головоломка нашего времени – кубик Рубика – начала своё победное шествие по свету с 1978 года, когда с ней впервые ознакомились математики на Международном математическом конгрессе в Хельсинки. Лишь несколько кубиков увезли математики с конгресса, но это стало начальным толчком лавинного распространения игрушки по всему миру.
Практически каждый может собрать одну грань кубика Рубика, но чтобы составить его полностью, часто приходится серьёзно задуматься. Собирая первую грань (или первый слой), можно не заботиться об остальных, но когда остаётся поменять местами последние несколько кубиков, очень легко всё испортить и начинать сначала.
Кубик-Рубик относится к вращательным головоломкам, отличительной чертой которых является то, что запутать их проще простого, а вот также быстро собирать их умеет далеко не каждый. далее назад

При запутывании мы действуем как попало и стараемся испортить сразу всё, при сборке же охватить сразу всю картину слишком сложно, нам удобнее продвигаться методично, шаг за шагом, устанавливая сначала один кусочек, подгоняя к нему второй и т. д. По мере выстраивания правильной картины свобода наших действий ограничивается, ведь достигнутое надо на последующих шагах сохранять. А ближе к концу сборки очередные продвижения уже невозможны без жертв, – мы вынуждены на время отдавать завоёванное с тем, чтобы вернуть его с прибылью. Здесь уже требуются специально разработанные операции, можно назвать их “локальными” или “минимальными”, которые вносят в расположение элементов головоломки самые малые изменения, например, переставляют два-три элемента или переворачивают их. При этом “минимальные” не значит “маленькие” - обычно они состоят из довольно большого числа ходов.
Рассмотрим алгоритм собирания вращательных головоломок на примере кубика Рубика.
назад

Формулы операций в “Кубике- Рубике”
При использовании “минимальных” операций возникает естественный вопрос: как их систематизировать или сформулировать, чтобы ими удобно было пользоваться при собирании кубика. Прежде всего, перед тем, как воспользоваться той или иной уже разработанной операцией, следует как-то обозначить грани кубика, относительно которых их проводить. Стандартные их названия: фасад, тыл, лево, право, верх, низ. А обозначения соответственно: Ф, Т, Л, П, В, Н. Любую формулу операций можно выполнить с помощью поворотов боковых или центральных граней кубика. Один поворот грани по часовой стрелке обозначается так же, как и сама грань (Ф, Т и т. д.). Если грань поворачивают против часовой стрелки, то к обозначению этого действия приписывают знак ’ (Ф’, Т’ и т. д.). Понятно, что два поворота по часовой стрелке идентичны двум поворотам против, а следовательно обозначаются они одинаково: знаком 2.­­­­­­ (Ф2, Т2 и т. д.).
далее назад

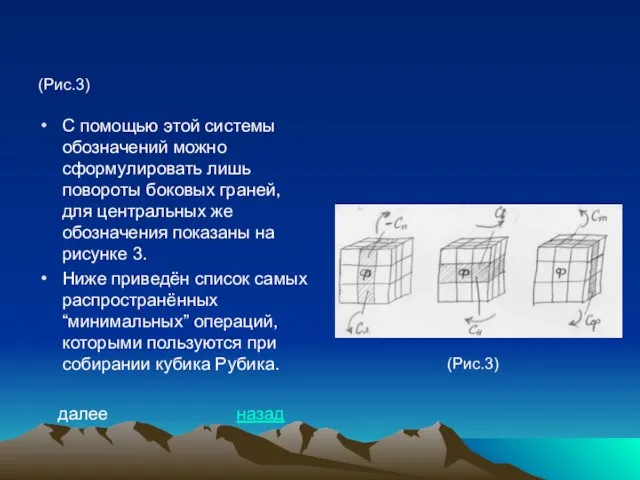
(Рис.3)
С помощью этой системы обозначений можно сформулировать лишь повороты боковых граней, для центральных же обозначения показаны на рисунке 3.
Ниже приведён список самых распространённых “минимальных” операций, которыми пользуются при собирании кубика Рубика.
далее назад
(Рис.3)

Следует заметить, что это лишь универсальные комбинации, а для создания более совершенного алгоритма собирания кубика, нужно разработать более “глобальные” операции, которые человеку запомнить довольно трудно, но в общем уменьшающие количество действий, необходимых для собирания кубика из каждого конкретного положения.
далее назад

Первый слой
Операция “лесенка” (лифт) 1:
Н’П’НП
Операция “лесенка” (лифт) 2:
НЛН’Л’
Сложная лесенка:
Н’П’Н2П
далее назад

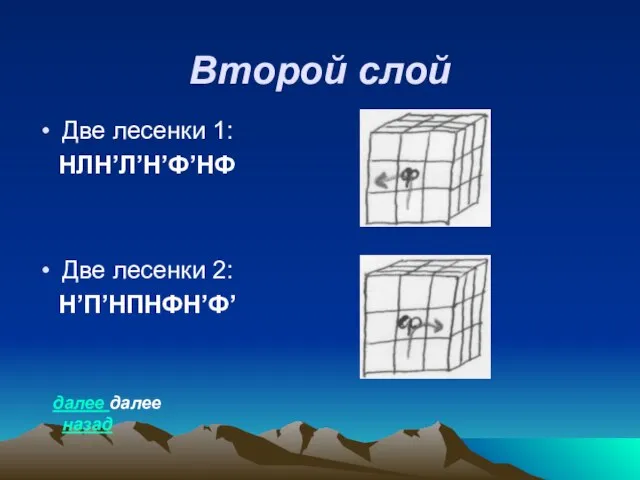
Второй слой
Две лесенки 1:
НЛН’Л’Н’Ф’НФ
Две лесенки 2:
Н’П’НПНФН’Ф’
далее далее назад

Третий слой
Выполняются только по две комбинации с поворотом верхней грани между ними:
(ПСн)4
Операция “Обмен” 1:
Ф2В’СпВ2СлВ’Ф2
Операция “Обмен” 2:
Л’Т’П’ТЛТ’ПТ
(Ф’ПФП’)2
Две последние операции выполняются лишь парами, либо по отдельности, но по два раза подряд с возможным поворотом верхней грани между комбинациями
(ПФ’П’Ф)2
назад

Пятнашки
До изобретения кубика Рубика для многих людей знакомство с головоломками начиналось с “пятнашек” – так часто называют известную игру “15”.
С пятнашек начинается история игр с дыркой – головоломок, в которых фишки перемещаются по игровому полю за счёт того, что одно из мест на поле свободно. У “пятнашек” есть множество родственников, которые как раз и образовывают целый раздел этих головоломок.
Игру “15” придумал в 70-х годах XIX-го века прославленный американский изобретатель головоломок Сэмюэль Лойд. Время появления его игрушки и известного всем кубика Рубика разделяют ровно сто лет. Любопытно, что возраст обоих изобретателей, когда они придумали свои знаменитые головоломки, был одинаков – немногим больше тридцати. До “пятнашек” никакая другая головоломка таким успехом не пользовалась.
далее далее назад

Великий Марк Твен, будучи современником Лойда и свидетелем всеобщего ажиотажа вокруг игры “15”, включил в свою сатирическую повесть “Американский претендент” изложение сообщения, якобы переданного агентством “Ассошиэйтед пресс”, в котором говорилось, что “за последние несколько недель вошла в моду новая игрушка-головоломка... и что от Атлантического океана до Тихого все население Соединенных Штатов прекратило работу и занимается только этой игрушкой; что в связи с этим вся деловая жизнь в стране замерла, ибо судьи, адвокаты, взломщики, священники, воры, торговцы, рабочие, убийцы, женщины, дети, грудные младенцы,— словом, все с утра до ночи заняты одним-единственным высокоинтеллектуальным и сложным делом... что веселье и радость покинули народ,— на смену им пришли озабоченность, задумчивость, тревога, лица у всех вытянулись, на них появились отчаяние и морщины — следы прожитых лет и пережитых трудностей, а вместе с ними и более печальные признаки, указывающие на умственную неполноценность и начинающееся помешательство; что в восьми городах день и ночь работают фабрики, и все же до сих пор не удалось удовлетворить спрос на головоломку”.
далее назад

Вскоре после своего появления на свет коробочка с цифрами 15 на крышке пересекла океан, быстро распространилась во всех европейских странах и поучила новое имя “такен”. Изобретателю посчастливилось найти ту неуловимую меру сложности, когда головоломка решалась без труда почти всеми и в то же время требовала определённой сообразительности, благодаря чему каждый мог получить удовольствие от сознания своего высокого интеллектуального уровня.
далее назад

Первому успеху головоломки в немалой степени способствовало и напечатанное в газетах объявление о призе в 1000$ за решение следующей задачи: в исходной позиции фишки располагаются по порядку номеров, за исключением двух последних, которые переставлены местами друг с другом (рис. 4); передвигая по одной фишке, но не вынимая фишки из коробочки, нужно поменять местами номера 15 и 14 так, чтобы все фишки стояли по порядку номеров, а правый нижний угол был свободен.
далее назад

Помещая это объявление, Ллойд знал, что ничем не рискует, так как предлагает неразрешимую задачу. Эта задача ещё сыграла с изобретателем
злую шутку, когда он пытался запатентовать свою игру, – ему сказали, что нельзя запатентовать. игру, не имеющую решения.
назад

Секрет игры “15”
Не всегда можно головоломку перевести из одного состояния в другое, — запрещены такие переходы, при которых нарушаются те или другие законы сохранения. Есть такой закон и в игре “15”. Чтобы объяснить его, мысленно заполним пустое место фишкой с номером 16. Тогда каждый ход — сдвиг фишки — будет состоять в том, что эта фишка меняется местами с фишкой 16. Операцию, при которой какие-то две фишки (не обязательно соседние!) меняются местами, так и назовем — обменом; математический термин для таких операций — транспозиция. Очевидно, что из любой расстановки 16 фишек можно не более чем за 15 обменов получить правильную позицию — обозначим ее S0 — и вообще любую другую расстановку. При этих обменах не запрещается вынимать фишки из коробки. Например, можно сначала поставить на свое место фишку 1, обменяв ее с той фишкой, которая это место занимает, затем точно так же поставить на место фишку 2 и т. д.
далее далее назад

Последними мы обменяем фишки 15 и 16 — при этом сразу обе встанут правильно. Конечно, не исключено, что по ходу дела какие-то фишки автоматически попадут на свои места, и их трогать не придется, при этом число обменов окажется меньше 15. Можно расставлять фишки по этой же системе, но в другом порядке, скажем 16, 15, 14, .... или совсем иначе, и тогда число обменов может оказаться другим. Однако, каким бы способом ни выбрать последовательность обменов, превращающую одну заданную расстановку фишек в другую, четность числа обменов в этой последовательности всегда будет одной и той же.
далее назад

Это очень важное и неочевидное докажем ниже. Оно позволяет дать следующее определение: расстановка называется четной, если ее можно превратить в правильную позицию с помощью четного числа обменов, и нечетной в противном случае. В математике обычно говорят не “расстановка”, а “перестановка”; к этому мы еще вернемся. Сама правильная расстановка S0 всегда четная, а ловушка Лойда L нечетная. Но почему они не переводятся друг в друга?
Как выше уже сказано, каждый ход в игре “15” можно рассматривать как обмен фишки с одной из соседних. Следовательно, при каждом ходе четность расстановки 16 фишек меняется: если до хода расстановку можно было упорядочить за N обменов, то после него — за N+1 обменов (взяв этот ход назад), а числа N и N+1 — разной четности. В обеих расстановках классической задачи Лойда дырка (или фишка 16) расположена одинаково.
далее далее назад

Если бы мы сумели одну расстановку перевести в другую, то фишка 16 должна была совершить столько же ходов вверх, сколько вниз, и столько же ходов вправо, сколько влево, иначе она не вернулась бы назад. Поэтому мы сделали бы четное число ходов, а так как при каждом ходе четность расстановки меняется, в начале и в конце она была бы одинаковой. Но позиции S0 и L, как мы видели, имеют разную четность.
назад

Мы рассмотрели лишь малую часть замечательных головоломок, которые придумали математики разных времён, но если когда-нибудь ещё и изобретут головоломку более популярную, чем, например, игра “15”, то известней знаменитого Кубика-Рубика наверняка – нет!
назад

Выводы