Математика в компьютерной графике

Базовые понятия
свободные векторы, радиус векторы, операции с векторами, скалярное и векторное произведение векторов (vector dot & cross production)
базис, координаты, декартова система координат
матрицы, операции с матрицами, обращение матриц

Преобразования (transformations)
Аффинные
Перспективные
Билинейные

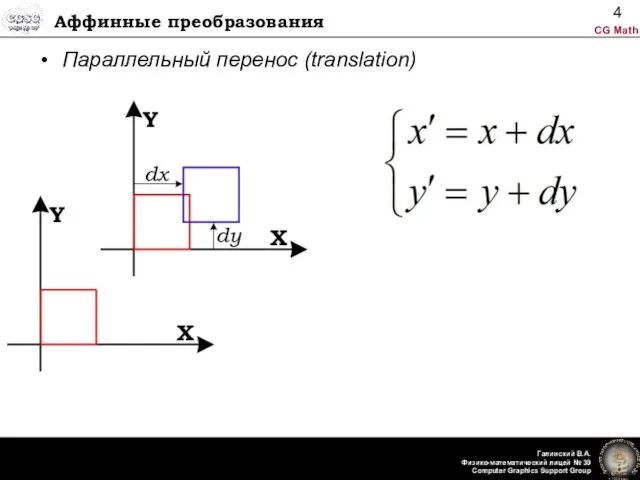
Аффинные преобразования
Параллельный перенос (translation)

Аффинные преобразования
Масштабирование (scaling)

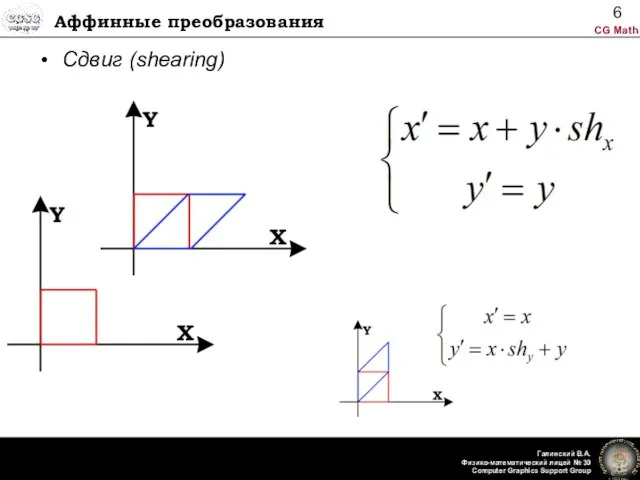
Аффинные преобразования
Сдвиг (shearing)

Аффинные преобразования
Масштабирование (scaling)

Аффинные преобразования
Поворот относительно начала координат (rotation)
r

Матричная запись аффинных преобразований
Перепишем в матричном виде общую запись аффинных преобразований:

Однородные координаты (homogeneous)
представим координаты на плоскости (2D) трехкомпонентной вектор - строкой:
будем полагать w = 1
перепишем преобразование в общем виде:

Матричный вид аффинных преобразований
~ translation
~ translation
~ shear by x
~ shear by y
~ rotation
~ scaling

Композиция преобразований
подвергнем точку последовательным преобразованиям системы координат:
перепишем:
в силу ассоциативности:

Обратные аффинные преобразования

Преобразование точек, векторов и нормалей
точка (радиус-вектор) (p):
вектор (v) и нормаль (n) (только направление):
преобразования:

Преобразование нормалей

Нотации записи: столбец или строка
Одно преобразование:
Композиция преобразований:

Пример: привязка систем координат
заданы точки соответствия
найти «матрицу перехода»

Пример: привязка систем координат

Пример: преобразование изображений
Поворот и
масштабирование
=> Прямое отображение (direct mapping) =>
<= Обратное отображение (inverse mapping) <=

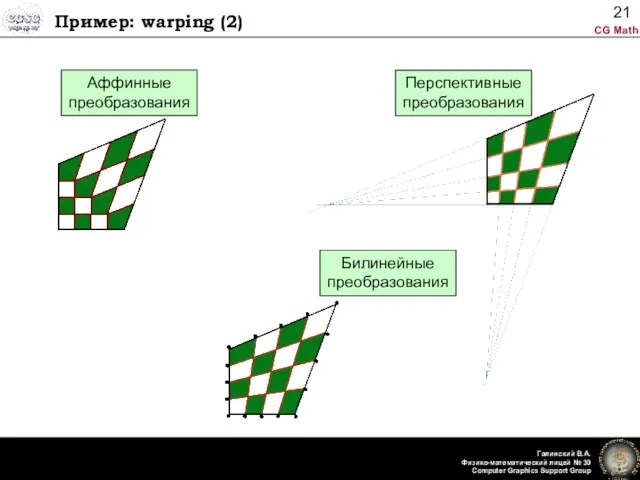
Пример: warping (1)

Пример: warping (2)
Аффинные
преобразования
Билинейные
преобразования
Перспективные
преобразования

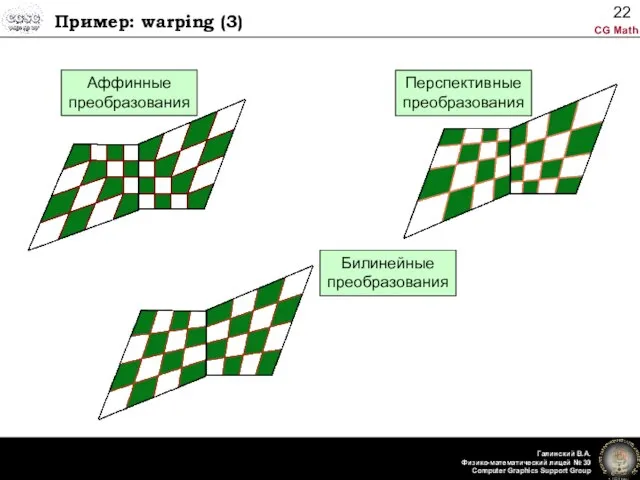
Пример: warping (3)
Аффинные
преобразования
Билинейные
преобразования
Перспективные
преобразования

Пример: morphing
morphing = warping + интерполяция цвета

Перспективные преобразования

Привязка с перспективным преобразованием (1)
общая формула:
прямое отображение:
полагаем w=1, итоговая формула для координат:

Привязка с перспективным преобразованием (2)
получаем матрицу обратного отображения
определитель присутствует и в числителе и в знаменателе – вычислять не нужно:
находим присоединенную матрицу:

Привязка с перспективным преобразованием (3)
Задача привязки: по 4 точкам соответствия определить матрицу перехода:

Привязка с перспективным преобразованием (4)
запишем зависимость (выразим координаты x и y):
выпишем в матричной форме 8 уравнений:

Привязка с перспективным преобразованием (5)
для упрощения задачи переход ищем из единичного квадрата:
получаем:

Привязка с перспективным преобразованием (6)
обозначаем:
и находим решение:

Аффинные преобразования в пространстве
Аналогично случаю 2D вводим однородные координаты:
и преобразования в общем случае:

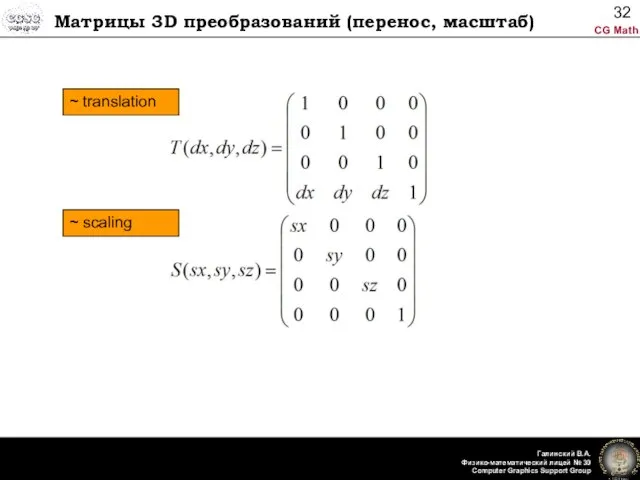
Матрицы 3D преобразований (перенос, масштаб)
~ translation
~ scaling

Матрицы 3D преобразований (поворот вокруг осей)
~ rotation

Матрицы 3D преобразований (поворот вокруг оси)
Поворот вокруг произвольной оси, проходящей через начало координат. Ось задается нормированным радиус вектором. Вывод через кватернионы (самостоятельно).
~ rotation

Пример: построение матрицы камеры (1)
камера задается: позиция С и векторы направление «вверх» V, «враво» U и вперед N.
ищем преобразование в виде «перенос+поворот»:
где

Пример: построение матрицы камеры (2)
после преобразования вектора отобразятся:
т.е.

Пример: построение матрицы камеры (3)
зная
находим