ОПТИМИЗАЦИЯ ПЕРЕЛЕТОВ ПРИ ОГРАНИЧЕНИЯХ НА НАПРАВЛЕНИЕ ТЯГИ

Отсутствие ограничений на направление тяги
p0, pr, pv, λα – сопряженные переменные
pv – базис-вектор Лоудена
Минимизируемый функционал:
Функция Гамильтона:
Уравнения движения:
α − вектор тяги
Оптимальная тяга при
Возможно ограничение:

ПСИОР
Оптимальная тяга
Функция переслючения
ИРТОМ
m = m(t) – масса КА
N = N(r, t) – мощность тяги
с − скорость истечения
1. Идеально регулируемая тяга ограниченной мощности (ИРТОМ)
2. Постоянная скорость истечения с ограниченным расходом рабочего тела (ПСИОР) или импульсная тяга
Отсутствие ограничений на направление тяги

Проекция вектора на множество
Проекция (абсолютная) вектора b на вектор a:
Проекция bA вектора b на некоторое замкнутое множество векторов A есть проекция на вектор a ∈ A , на котором достигается max bTa0.
Матрица Р проектирует b на множество А.
P = a0a0T − проективная матрица
Проекцию bi вектора b на вектор ai ∈ A (i = 1, 2, …) назовем локальной проекцией на множество A , если существует такая окрестность вектора ai , что для любого вектора aε из этой окрестности

Свойства проекций вектора на множество

Общий случай ограничений на направление тяги
Максимум функции Гамильтона достигается при
Матрица проектирует вектор pv на множество G
pG = Ppv − проекция pv на G
G
⇒ pG = pv
⇒ pG лежит на границе G
⇒ достаточно проверить
G
При ограничении g = 0 граница множества совпадает с самим множеством.
Ограничения на единичный вектор α0 направления тяги:
α0 ∈ G, G: g = 0 или g ≥ 0, g = g(r, v, t, α0)

Оптимальная тяга
Ограничения на направление тяги
ИРТОМ
ПСИОР
Отсутствие ограничений

Ограничение типа равенства
− делает систему автономной

Ограничение типа неравенства
Граница множества G: k компонент вектора g равны нулю, а остальные n – k компонент строго больше нуля (1 ≤ k ≤ n)
Двусторонние ограничения разбиваются на два неравенства
g = {g1, …, gn},
G = G1∩ G2 ∩...∩ Gn
Если , то pG = pv
Рассмотрим случай , когда pG на границе G
Границы подмножеств Gi могут пересекаться либо не пересекаться (например, в случае двусторонних ограничений)

Пусть для каждой пары gi, gj одновременное выполнение равенств
gi = 0, gj = 0
либо возможно лишь для конечного числа значений α0, либо невозможно.
Способ нахождения оптимального α0 при :
Вычисляются все проекции вектора pv на подмножества Gi
Находятся точки пересечения границ каждой пары подмножеств Gi, Gj
Из всех найденных векторов α0 выбираются принадлежащие пересечению G и среди них находится
Ограничение типа неравенства

Линейные ограничения типа равенства
G: Bα0 = c B = B(r, v, t), c = c(r, v, t)
− проективная матрица (проектирует ⊥ В), I − единичная матрица
− оптимальное направление тяги
ограничение типа равенства дает поверхность конуса при n = 1 или линии пересечения поверхностей круговых конусов при n = 2; матрица ВВТ невырожденна если конусы пересекаются
Ограничение выполнимо лишь при |ci| ≤ |bi|

Линейные ограничения типа неравенства
G: Bα0 ≥ c B = B(r, v, t), c = c(r, v, t)
Gi: ⇒ α0 внутри (ci > 0) или вне (ci < 0) кругового конуса,
− пересечение круговых конусов.
⇒ оптимальное направление тяги достигается либо на поверхности i-го конуса, либо на линии пересечения двух конусов
или
Пусть

Линейные однородные ограничения
− проективная матрица
Bα0 = 0 B = B(r, v, t) − матрица ранга 1 (плоскость) или 2 (прямая)
⇒ Оптимальная тяга либо направлена вдоль заданного вектора, либо ортогональна заданному вектору

Линейные однородные ограничения
типа неравенства
Bα0 ≥ 0 − телесный угол, ограниченный плоскостями (полупространство, если В строка)
⇒ оптимальное направление тяги достигается либо на i-й плоскости, либо на линии пересечения двух плоскостей

Примеры линейных однородных ограничений

Объединение множеств и смешанные ограничения
Приведенные результаты легко обобщаются на:
Объединение ограничивающих множеств G = G1∪ G2∪ … ∪ Gn
Пример: bTα0 ≥ c > 0 или bTα0 ≤ −c

Уравнения для базис-вектора Лоудена

Способы вычисления базис-вектора Лоудена
Численное интегрирование совместно с уравнениями движения
На больших интервалах времени приближенные методы могут расходиться

Метод транспортирующей траектории
Метод транспортирующей траектории (МТТ) – метод приближенного решения задачи оптимального перелета с ИРТОМ, основанный на линеаризации траектории перелета около некоторой близкой кеплеровской орбиты (транспортирующей траектории − ТТ)
Модифицированный МТТ:
x, y − векторы состояния КА и транспортирующей траектории,
ξ0, ξ1 − граничные условия,
A − общее решение сопряженного уравнения в вариациях для ТТ (найдено аналитически в явном виде)
Q − подматрица матрицы А
Δ = А1ξ1 − А0ξ0, А0 = А(t0), А1 = А(t1)

Метод транспортирующей траектории
Матрица QQT вырожденна, однако матрица S является невырожденной на любом интервале времени
оптимальная тяга
вектор состояния КА
минимизируемый функционал
масса рабочего тела
Любая требуемая точность достигается путем разбиения интервала времени перелета на подынтервалы.
, β = const − неизвестный вектор

Применение МТТ при ограничениях на направление тяги
В общем случае Р зависит от pv = QTβ ⇒ β находится из уравнения
и
В случае линейных однородных ограничений Вα0 = 0 матрица Р не зависит от β
⇒ Невырожденность матрицы S1 является достаточным условием осуществимости перелета при данных ограничениях

Пример: радиальная тяга
где q = {q1, …, q6} = Qr/r
q1 = q2 = 0 ⇒ rank S1≤ 4
Плоский перелет: Δ1 = Δ2 = 0 (полагая Δ = {Δ1, …, Δ6})
Уменьшение размерности:
Δ′ = {Δ3, …, Δ6}, q′ = {q3, …, q6}, β′ = {β3, …, β6}
Матрица может быть невырожденной
⇒ условие невырожденности матрицы S1 может не быть необходимым для осуществимости перелета
Применение МТТ при ограничениях на направление тяги

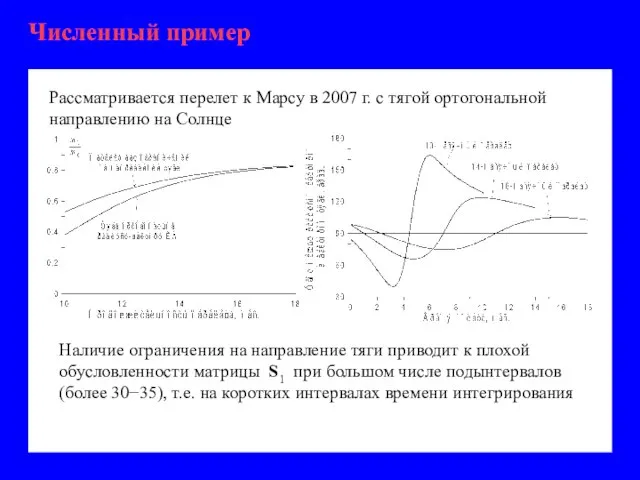
Численный пример
Рассматривается перелет к Марсу в 2007 г. с тягой ортогональной направлению на Солнце
Наличие ограничения на направление тяги приводит к плохой обусловленности матрицы S1 при большом числе подынтервалов (более 30−35), т.е. на коротких интервалах времени интегрирования