Метод интервалов. Общий метод интервалов

Литература С.М. Никольский «Алгебра и начала анализа: Учебник для 10 класса общеобразовательных учреждений» §2 п. 2.7 – 2.9.

Определение

+
-
+
-
+

Метод интервалов для решения неравенств вида
, , , ,
где , ,
, то есть все различны.

3. Над промежутком справа от наибольшего нуля многочлена поставить знак «+», так как на этом промежутке все множители положительны. Затем, двигаясь справа налево, при переходе через очередной нуль, сменить знак на противоположный.

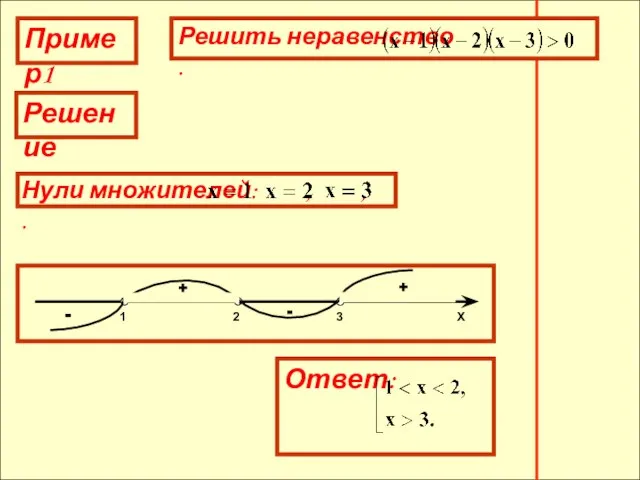
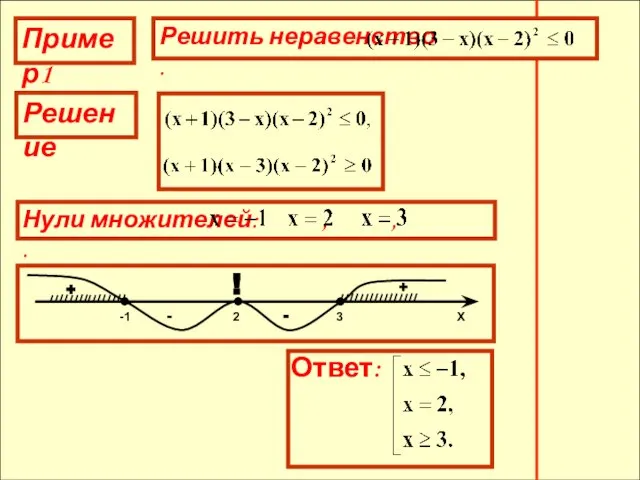
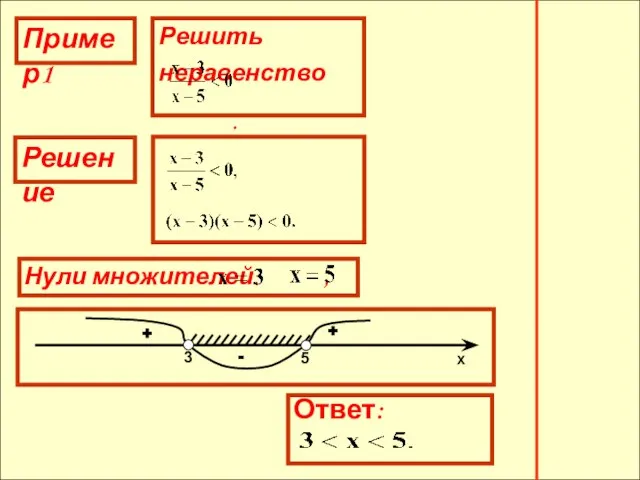
Пример1
Решение
+
-
+
-

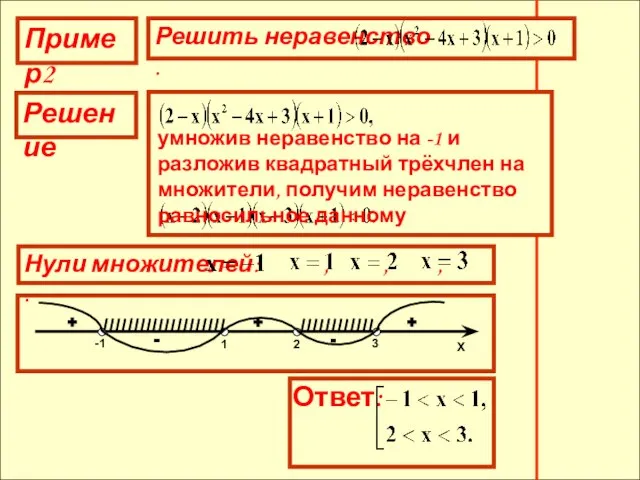
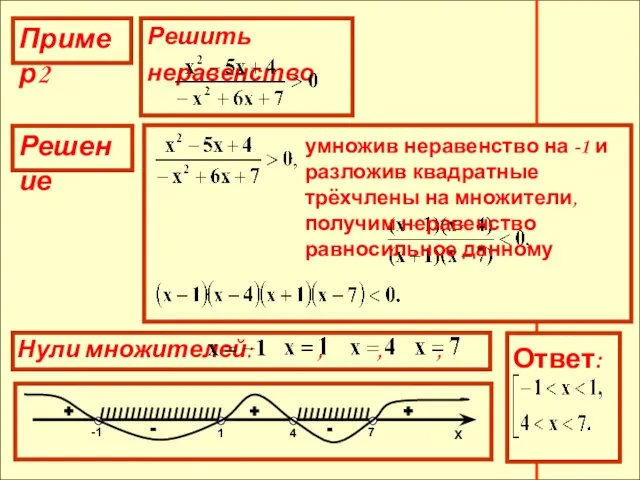
Пример2
Решение
умножив неравенство на -1 и разложив квадратный трёхчлен на множители, получим неравенство равносильное данному
Нули множителей: , , , .
+
-
+
-
+

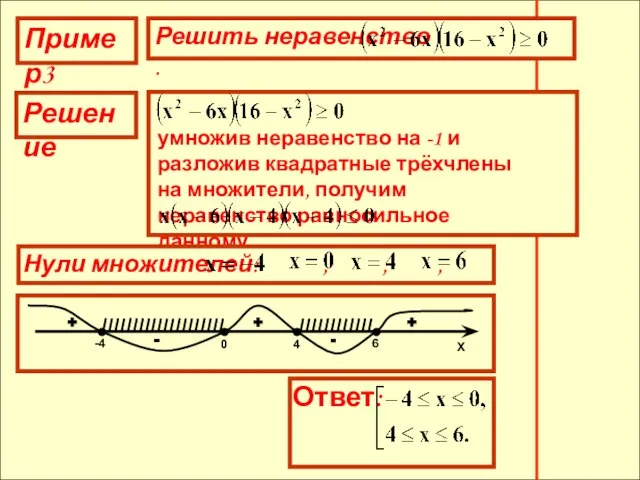
Пример3
Решение
умножив неравенство на -1 и разложив квадратные трёхчлены на множители, получим неравенство равносильное данному
Нули множителей: , , , .
+
+
-
-
+

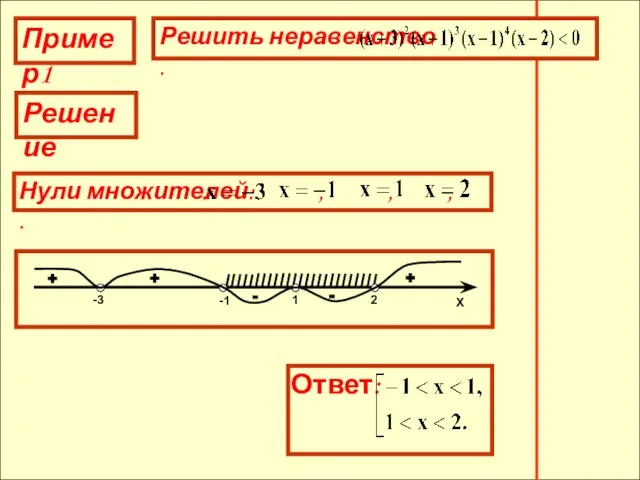
Пример4
Решение
Нули множителей: , , , , , .
+
+
+
+
-
-
-

Общий метод интервалов для решения неравенств вида , , , ,где , если не все различны.

Общий метод интервалов для решения неравенств вида , , , ,где , если не все различны.
3. Над промежутком справа от наибольшего нуля многочлена поставить знак «+», так как на этом промежутке все множители положительны. Затем, двигаясь справа налево, при переходе через очередной нуль, сменить знак на противоположный, если соответствующий этому нулю двучлен возведён в нечётную степень, и сохранить знак, если соответствующий этому нулю двучлен возведён в чётную степень.

Решение
Нули множителей: , , , .
+
+
-
-
+

+
-
-
+

Нули множителей: , .
+
+
-

умножив неравенство на -1 и разложив квадратные трёхчлены на множители, получим неравенство равносильное данному
Нули множителей: , , , .
+
-
+
-
+

Нули множителей: , , , .
+
-
+
-
+

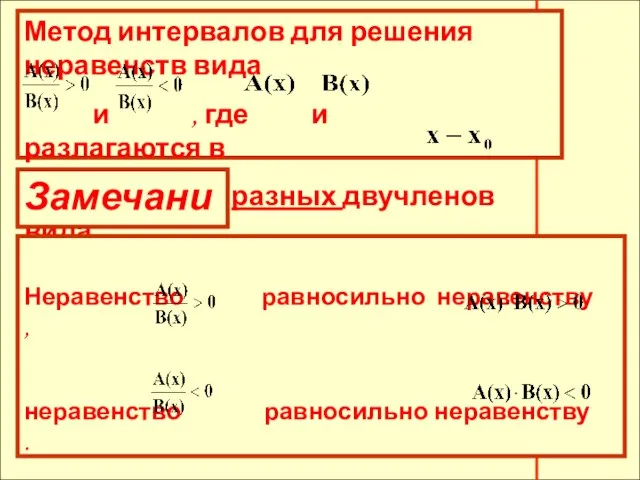
Метод интервалов для решения неравенств вида
и , где и разлагаются в
произведения двучленов, где в числителе и знаменателе дроби имеются одинаковые двучлены .

Нули множителей: , , .
+
-
-
+

Нули числителя: , .
Нули знаменателя: , , .
+
+
+
-
-
-