Содержание
- 2. Прямоугольная декартовая система координат по имени французского математика Рене Декарта Любая информация , в том числе
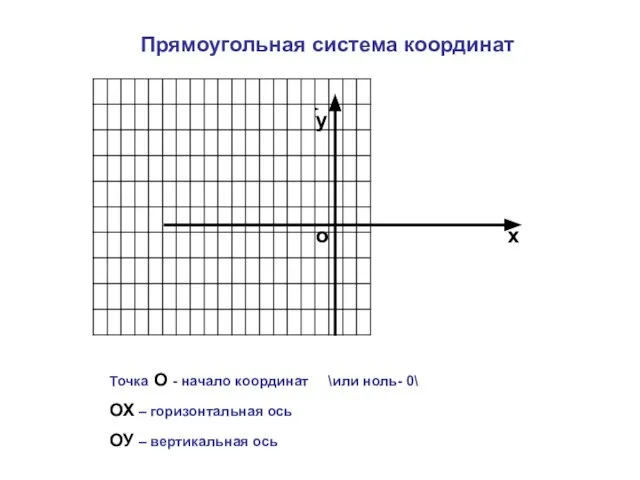
- 3. о х у Прямоугольная система координат Точка О - начало координат \или ноль- 0\ ОХ –
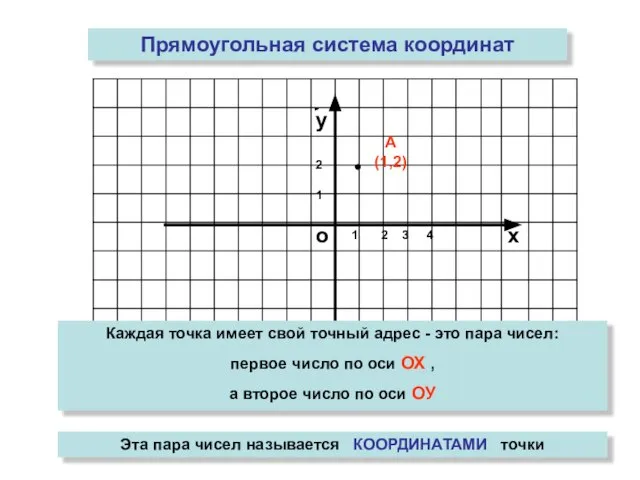
- 4. о х у Прямоугольная система координат 1 Каждая точка имеет свой точный адрес - это пара
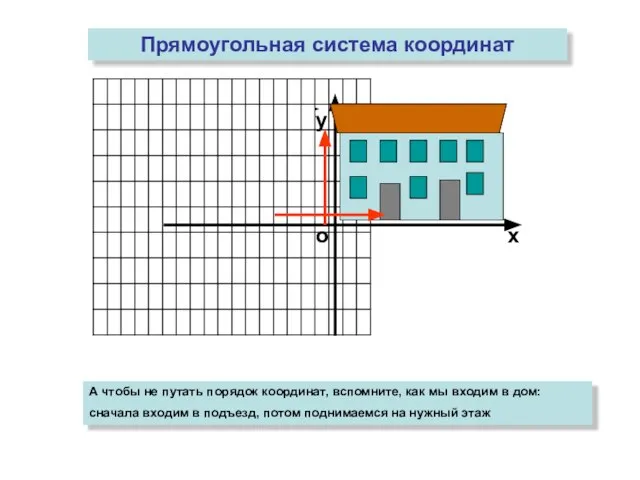
- 5. о х у Прямоугольная система координат А чтобы не путать порядок координат, вспомните, как мы входим
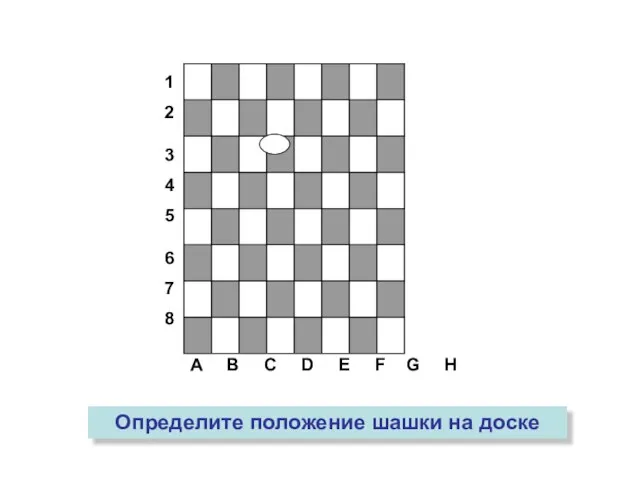
- 6. A B C D E F G H 1 2 3 4 5 6 7 8
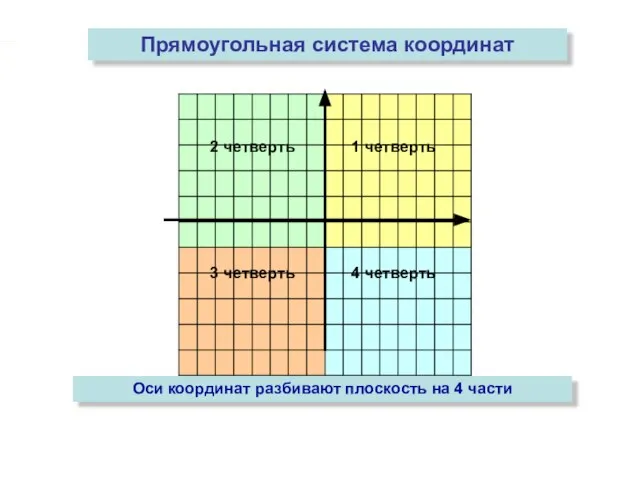
- 7. 2 четверть 1 четверть 3 четверть 4 четверть Прямоугольная система координат Оси координат разбивают плоскость на
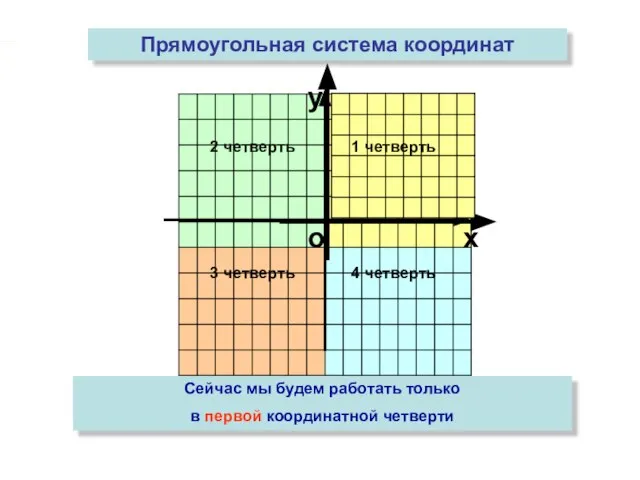
- 8. 2 четверть 3 четверть 4 четверть Прямоугольная система координат Сейчас мы будем работать только в первой
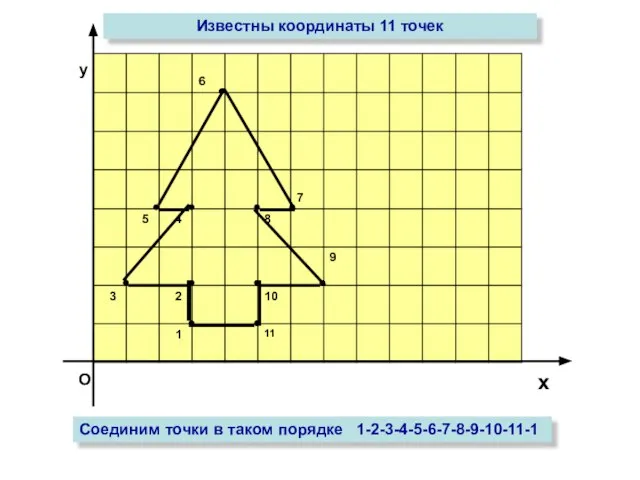
- 9. О х у Известны координаты 11 точек Соединим точки в таком порядке 1-2-3-4-5-6-7-8-9-10-11-1
- 10. Мы провели работу по декодированию графического изображения, которое состояло из 11 точек , соединенных отрезками. Эти
- 12. Скачать презентацию


 Умножение числа на сумму
Умножение числа на сумму Дидактическая игра по финансовой грамотности Четвёртый лишний
Дидактическая игра по финансовой грамотности Четвёртый лишний Беседа по рассказу Л.Н.Толстого Косточка
Беседа по рассказу Л.Н.Толстого Косточка Методы стимулирования труда
Методы стимулирования труда О проведении работы по медицинскому обеспечению летней оздоровительной кампании 2012 года в Пермском крае
О проведении работы по медицинскому обеспечению летней оздоровительной кампании 2012 года в Пермском крае УСПЕШНАЯ ЛИЧНОСТЬ
УСПЕШНАЯ ЛИЧНОСТЬ ДЕНЬГИ ДЛЯ МЕНЯ – ЭТО… - презентация
ДЕНЬГИ ДЛЯ МЕНЯ – ЭТО… - презентация Социально-педагогические технологии работы с неблагополучной семьёй.
Социально-педагогические технологии работы с неблагополучной семьёй. Об итогах реализации областной адресной программы «Проведение капитального ремонта многоквартирных домов на территории Ульянов
Об итогах реализации областной адресной программы «Проведение капитального ремонта многоквартирных домов на территории Ульянов Мотивная структура стихотворения Иосифа Бродского «Все чуждо в доме новому жильцу…»
Мотивная структура стихотворения Иосифа Бродского «Все чуждо в доме новому жильцу…» Социология предпринимательства
Социология предпринимательства Технические навыки чтения
Технические навыки чтения Презентация на тему ЭСТОНИЯ (11 класс)
Презентация на тему ЭСТОНИЯ (11 класс)  ПЛАНкомплексного анализа стихотворения А.С.Пушкина «ПРОРОК»
ПЛАНкомплексного анализа стихотворения А.С.Пушкина «ПРОРОК» Современное состояние международной лицензионной торговли
Современное состояние международной лицензионной торговли Анмимация античного храма
Анмимация античного храма Островский как основоположник русского театра
Островский как основоположник русского театра Символика России
Символика России Тема 4
Тема 4 Попов Алексей ПетровичЛАЗЕРНАЯ ДИАГНОСТИКА СИЛЬНОРАССЕИВАЮЩИХ СРЕД И ИЗМЕНЕНИЕ ИХ ОПТИЧЕСКИХ СВОЙСТВПУТЕМ ИМПЛАНТАЦИИ НАНОЧА
Попов Алексей ПетровичЛАЗЕРНАЯ ДИАГНОСТИКА СИЛЬНОРАССЕИВАЮЩИХ СРЕД И ИЗМЕНЕНИЕ ИХ ОПТИЧЕСКИХ СВОЙСТВПУТЕМ ИМПЛАНТАЦИИ НАНОЧА Домашняя косметика – путь к гармонии
Домашняя косметика – путь к гармонии Возрастные особенности подросткового возраста
Возрастные особенности подросткового возраста Жил-был один богатый купец и у него было...
Жил-был один богатый купец и у него было... Кому это нужно? •Организациям •Государственным учреждениям •Школам, институтам, больницам •Провайдерам и домовым сетям
Кому это нужно? •Организациям •Государственным учреждениям •Школам, институтам, больницам •Провайдерам и домовым сетям История празднования Масленицы
История празднования Масленицы Сравнительный анализ кентавра и антикентавра
Сравнительный анализ кентавра и антикентавра Тайм-менеджемнт
Тайм-менеджемнт Никто не забыт, ничто не забыто
Никто не забыт, ничто не забыто