Содержание
- 2. Перпендикулярные прямые в пространстве Две прямые в пространстве называются перпендикулярными, если угол между ними равен 90°.
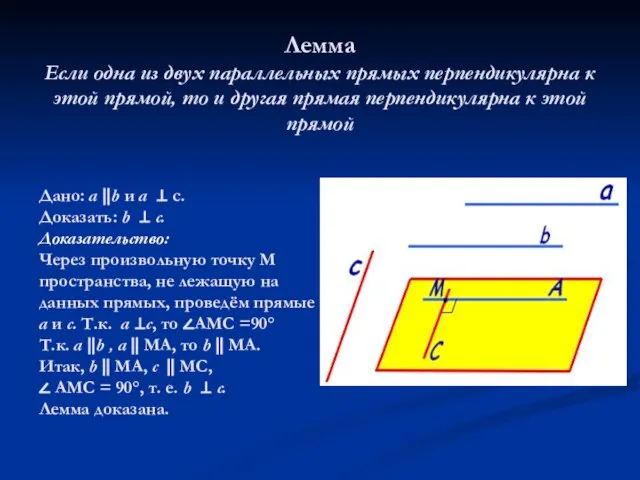
- 3. Лемма Если одна из двух параллельных прямых перпендикулярна к этой прямой, то и другая прямая перпендикулярна
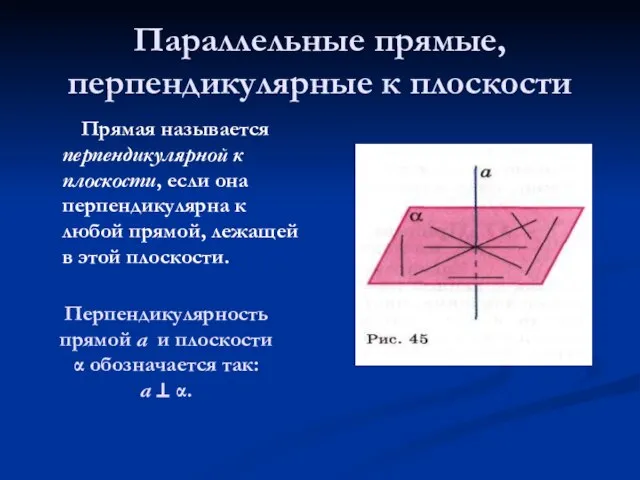
- 4. Параллельные прямые, перпендикулярные к плоскости Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой,
- 5. Теорема: Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к
- 6. Теорема: Если две прямые перпендикулярны к плоскости, то они параллельны. Дано: a ⊥α,b ⊥α (а) Доказать
- 7. Признак перпендикулярности прямой и плоскости Теорема: Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости,
- 8. Теорема о прямой, перпендикулярной к плоскости Теорема: Через любую точку пространства проходит прямая, перпендикулярная к данной
- 10. Скачать презентацию





 Архитектура XX-XIX века
Архитектура XX-XIX века Presentation Title
Presentation Title  Пути реализации инклюзивного образования средствами инновационной деятельности
Пути реализации инклюзивного образования средствами инновационной деятельности Дюралюминий. Сфера применения
Дюралюминий. Сфера применения Презентация на тему Вирусы неклеточные формы жизни
Презентация на тему Вирусы неклеточные формы жизни  Музыкальный шаблон для презентации
Музыкальный шаблон для презентации Частно-государственное партнёрство Проект по схеме BOOT («Строительство - Владение – Эксплуатация – Передача»)
Частно-государственное партнёрство Проект по схеме BOOT («Строительство - Владение – Эксплуатация – Передача») РЕАЛИЗАЦИЯ КОМПЛЕКСНОГО ПРОЕКТА МОДЕРНИЗАЦИИ СИСТЕМЫ ОРАЗОВАНИЯ
РЕАЛИЗАЦИЯ КОМПЛЕКСНОГО ПРОЕКТА МОДЕРНИЗАЦИИ СИСТЕМЫ ОРАЗОВАНИЯ ОЦЕНКА КАЧЕСТВА ОТЧЕТНОЙ ДОКУМЕНТАЦИИ ПО ОНКОЛОГИИСТАТИСТИЧЕСКИЙ УЧЕТ И ОТЧЕТНОСТЬ В УЧРЕЖДЕНИЯХ ОНКОЛОГИЧЕСКОГО ПРОФИЛЯ
ОЦЕНКА КАЧЕСТВА ОТЧЕТНОЙ ДОКУМЕНТАЦИИ ПО ОНКОЛОГИИСТАТИСТИЧЕСКИЙ УЧЕТ И ОТЧЕТНОСТЬ В УЧРЕЖДЕНИЯХ ОНКОЛОГИЧЕСКОГО ПРОФИЛЯ Kulttuuri ja kulttuurien välinen kompetenssi
Kulttuuri ja kulttuurien välinen kompetenssi Историческая игра
Историческая игра Основы православной культуры
Основы православной культуры 28 апреля – 1 мая 2011
28 апреля – 1 мая 2011 Гордимся прошлым, строим будущее
Гордимся прошлым, строим будущее Химические свойства кислот
Химические свойства кислот Как помочь ребёнку в выполнении домашних заданий
Как помочь ребёнку в выполнении домашних заданий Болезни цивилизации
Болезни цивилизации Отдел Кредитного Контроля: взаиморасчеты
Отдел Кредитного Контроля: взаиморасчеты Правонарушения – дорога в пропасть
Правонарушения – дорога в пропасть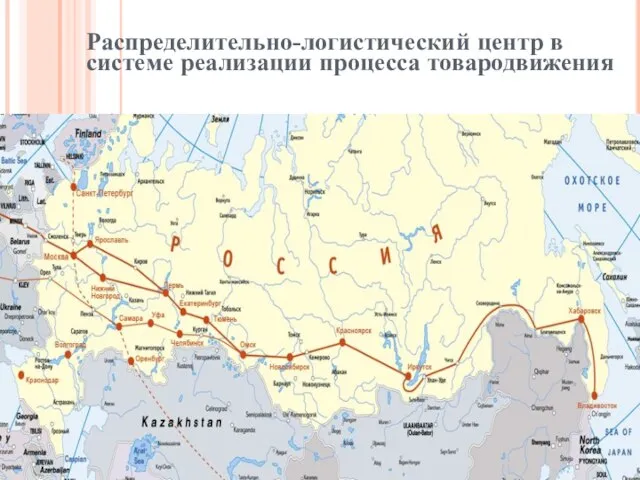 Распределительно-логистический центр в системе реализации процесса товародвижения
Распределительно-логистический центр в системе реализации процесса товародвижения СТРАХОВА КОМПАНІЯ “ІНДІГО”
СТРАХОВА КОМПАНІЯ “ІНДІГО” Принципы антибиотикотерапии в лечении инфекций МВП
Принципы антибиотикотерапии в лечении инфекций МВП Торговый алгоритм
Торговый алгоритм Цифровые приборы
Цифровые приборы Урок в музее «Русская изба» Слушаем, Размышляем, рисуем. - презентация
Урок в музее «Русская изба» Слушаем, Размышляем, рисуем. - презентация Программаинновационного развития ОАО «Аэрофлот – российские авиалинии».
Программаинновационного развития ОАО «Аэрофлот – российские авиалинии». Фрустрация и тревога как эмоциональное состояние.
Фрустрация и тревога как эмоциональное состояние. Модульная реклама в черно-белом варианте
Модульная реклама в черно-белом варианте