Содержание
- 2. Предмет математики настолько серьезен, что полезно не упускать случаев делать его немного занимательным. Великий французский математик,
- 3. Что такое сплайн? Под сплайном (от англ. spline — планка, рейка) обычно понимают кусочно-заданную функцию. Функции,
- 4. Введение Определение линейного сплайна Определение модуля Построение графиков Заключение Содержание
- 5. Графики функций широко используются в различных областях инженерных знаний, поэтому умение строить, “читать”, прогнозировать их “поведение”
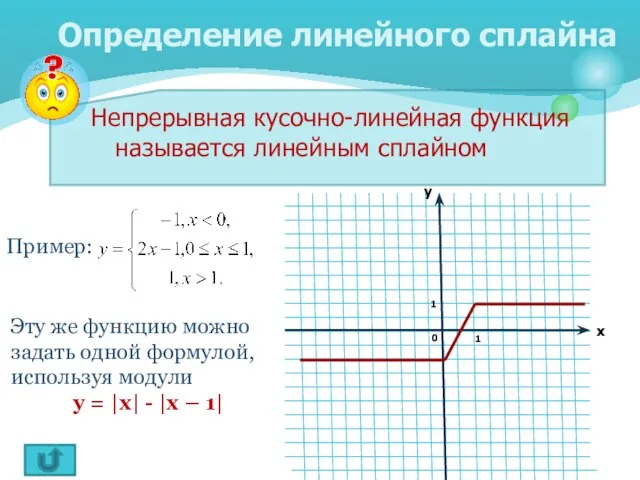
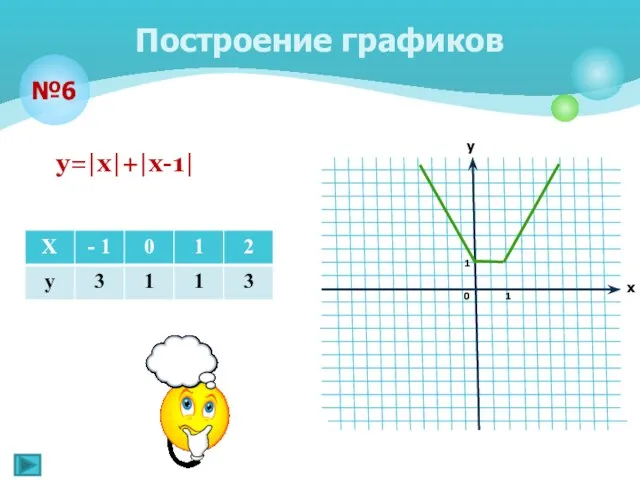
- 6. Непрерывная кусочно-линейная функция называется линейным сплайном Определение линейного сплайна Пример: Эту же функцию можно задать одной
- 7. Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера». Это многозначное слово (омоним),
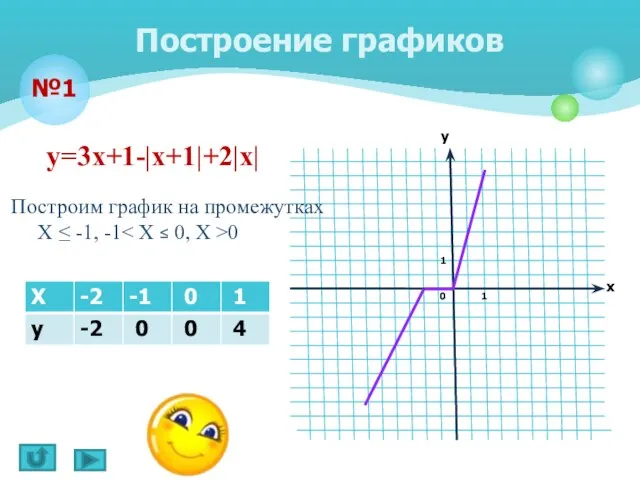
- 8. Построение графиков №1 у=3х+1-|х+1|+2|х| Построим график на промежутках Х ≤ -1, -1 0
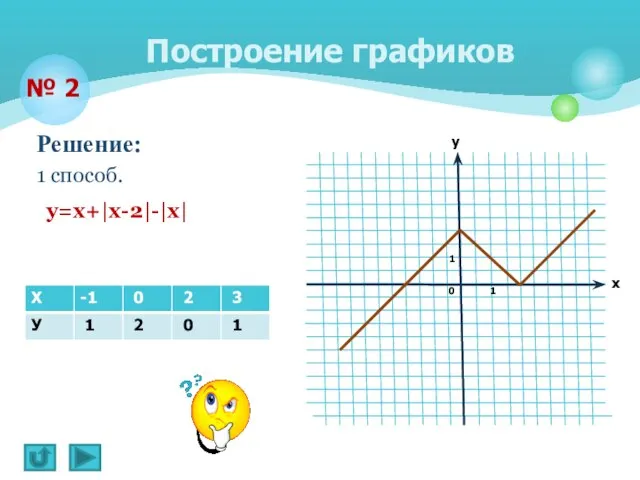
- 9. Решение: 1 способ. № 2 y=х+|х-2|-|х| Построение графиков
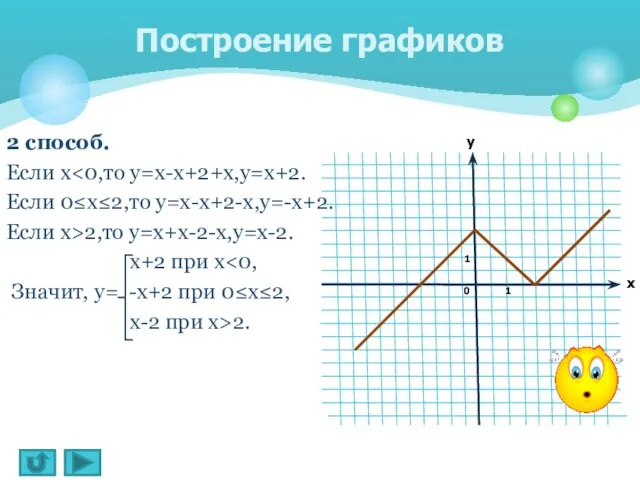
- 10. Построение графиков 2 способ. Если х Если 0≤х≤2,то у=х-х+2-х,у=-х+2. Если х>2,то у=х+х-2-х,у=х-2. х+2 при х Значит,
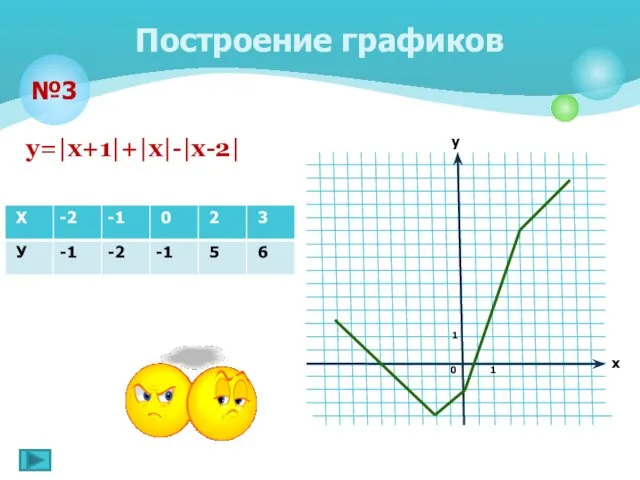
- 11. у=|х+1|+|х|-|х-2| Построение графиков №3
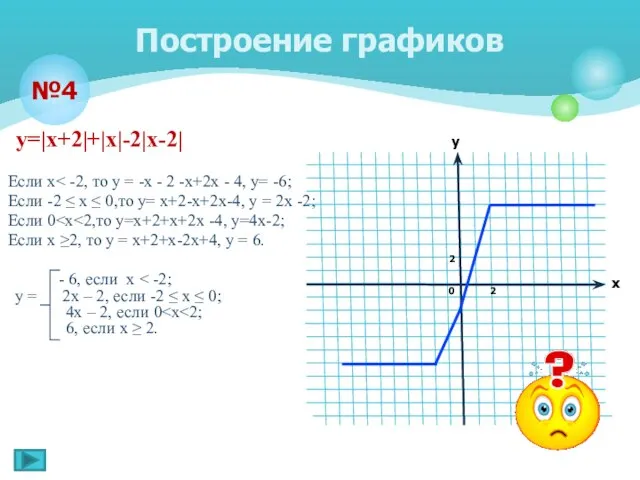
- 12. у=|х+2|+|х|-2|х-2| Если х Если -2 ≤ х ≤ 0,то у= х+2-х+2х-4, у = 2х -2; Если
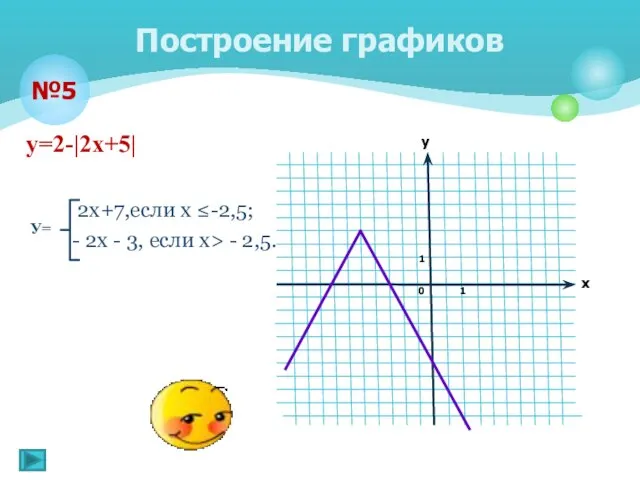
- 13. у=2-|2х+5| 2x+7,если х ≤-2,5; - 2х - 3, если х> - 2,5. Построение графиков №5 У=
- 14. Построение графиков №6 у=|х|+|х-1|
- 15. Мы узнали: Что называется линейным сплайном? Как строить графики, используя этот метод? Кем впервые был предложен
- 17. Скачать презентацию





 Психология образования
Психология образования Ежегодный отчёт директора школы по итогам 2011-2012 учебного года
Ежегодный отчёт директора школы по итогам 2011-2012 учебного года Типы экологических взаимодействий
Типы экологических взаимодействий Урок « На севере Европы»
Урок « На севере Европы» Риторическая компетенция как ведущее средство образования
Риторическая компетенция как ведущее средство образования Знаки приоритета
Знаки приоритета Примеры речевых форм эмоциональной экспрессии
Примеры речевых форм эмоциональной экспрессии Компьютерный подбор краски для автомобилей. Заправка аэрозольных баллонов краской. Подбор автоэмалей для ремонта царапин
Компьютерный подбор краски для автомобилей. Заправка аэрозольных баллонов краской. Подбор автоэмалей для ремонта царапин Презентация на тему Пути достижения биологического прогресса
Презентация на тему Пути достижения биологического прогресса  Адаптированная примерная основная образовательная программа для дошкольников
Адаптированная примерная основная образовательная программа для дошкольников  Электронные библиотеки и библиотеки: на пути к совершенным интеллектуальным поисковым системам Шрайберг Яков Леонидович, докто
Электронные библиотеки и библиотеки: на пути к совершенным интеллектуальным поисковым системам Шрайберг Яков Леонидович, докто Мексиканский медичи. Евгенио Лопез Алоносо
Мексиканский медичи. Евгенио Лопез Алоносо Важность инновационных продуктов в создании стоимости и качества активов в аптечном секторе
Важность инновационных продуктов в создании стоимости и качества активов в аптечном секторе Слово как культурообразующая сила. Князь Андрей Боголюбский и культурно-историческая среда
Слово как культурообразующая сила. Князь Андрей Боголюбский и культурно-историческая среда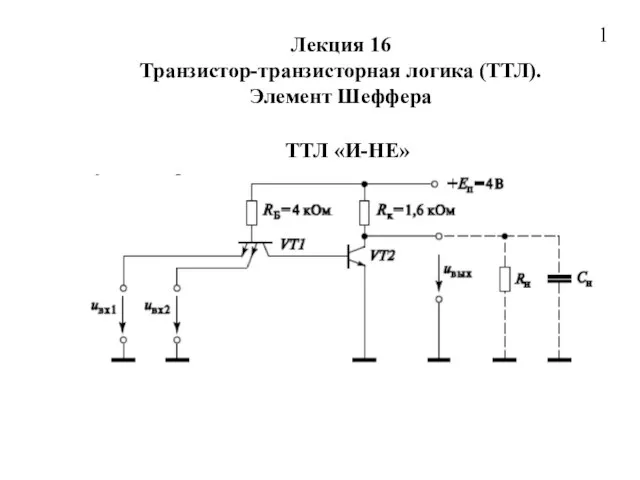 Элемент Шеффера
Элемент Шеффера  Информация об Ассоциации «Рекламная Федерация Регионов»
Информация об Ассоциации «Рекламная Федерация Регионов» Zhivoy_personazh_i_ego_arka
Zhivoy_personazh_i_ego_arka Методы проведения дискуссии
Методы проведения дискуссии  Погоны ВС РФ
Погоны ВС РФ Яндекс_Лавка
Яндекс_Лавка Культурное пространство империи первой половины XIX в
Культурное пространство империи первой половины XIX в Teacher’s Day
Teacher’s Day Знаки +,=,-
Знаки +,=,- Штукатурки цементные ВОЛМА
Штукатурки цементные ВОЛМА Податкові послуги на порталі Дія
Податкові послуги на порталі Дія Механические колебания и волны
Механические колебания и волны Презентация на тему Разделка рыбы
Презентация на тему Разделка рыбы