Содержание
- 2. ПРЕДМЕТНАЯ ОБЛАСТЬ В настоящее время в теории и практике аналитической деятельности получила большое развитие концепция сложных
- 3. ТРАДИЦИОННЫЕ ПОДХОДЫ Известно, что матрицы взаимосвязей понятий (МВП) являются одной из форм представления сетевых структур, аналогичной
- 4. Таблица взаимосвязи понятий
- 5. Коэффициент сцепления
- 6. Неявные связи (матрица скрытности)
- 7. Скрытые связи слов Слова считаются связанными, если они стоят рядом с текстом. Известно, что матрица инцидентности
- 8. Некоторые выводы Приведенный метод во многом напоминает подходы, базирующиеся на комбинаторном кластерном анализе, однако его принципиальное
- 10. Скачать презентацию
Слайд 2ПРЕДМЕТНАЯ ОБЛАСТЬ
В настоящее время в теории и практике аналитической деятельности получила большое
ПРЕДМЕТНАЯ ОБЛАСТЬ
В настоящее время в теории и практике аналитической деятельности получила большое

Описывается метод, позволяющий выявлять неявные связи в сложных сетях, представленных матрицами инцидентности.
Описывается применение данного метода, базирующегося на теории электрических сетей, для выявления силы взаимосвязей понятий, извлекаемых из неструктурированных текстов, в частности, персон.
Этот же метод может применяться, например, для выявления неявных связей терминов в текстах сообщений электронных СМИ.
Слайд 3ТРАДИЦИОННЫЕ ПОДХОДЫ
Известно, что матрицы взаимосвязей понятий (МВП) являются одной из форм представления
ТРАДИЦИОННЫЕ ПОДХОДЫ
Известно, что матрицы взаимосвязей понятий (МВП) являются одной из форм представления

Чаще всего ребрам этих графов приписываются весовые коэффициенты, которые пропорциональны количеству документов из некоторого массива, одновременно соответствующие обоим узлам (понятиям), соединяемым этими ребрами. Существуют и другие многочисленные подходы к определению близости понятий в массивах неструктурированных текстов, среди таких можно назвать контекстные, вероятностные и энтропийные (Mutual Information), но все они являются лишь предпосылками для построения матриц взаимосвязей, их перегруппировки и визуализации.
Известно, что матрицы взаимосвязей понятий (МВП) являются одной из форм представления сетевых структур, аналогичной по функциональности их графовому представлению. На практике эти матрицы чаще всего отражают близость отдельных понятий (совместную встречаемость в документах или близость по сопутствующему контексту в разных документах). При самых различных подходах к их построению - это, как правило, симметричные матрицы, элементы которых – коэффициенты взаимосвязей. Если отношения между понятиями не носят направленного характера, то их также можно рассматривать как неориентированные графы и применять к ним соответствующие методы.
Чаще всего ребрам этих графов приписываются весовые коэффициенты, которые пропорциональны количеству документов из некоторого массива, одновременно соответствующие обоим узлам (понятиям), соединяемым этими ребрами. Существуют и другие многочисленные подходы к определению близости понятий в массивах неструктурированных текстов, среди таких можно назвать контекстные, вероятностные и энтропийные (Mutual Information), но все они являются лишь предпосылками для построения матриц взаимосвязей, их перегруппировки и визуализации.
Слайд 4Таблица взаимосвязи понятий
Таблица взаимосвязи понятий
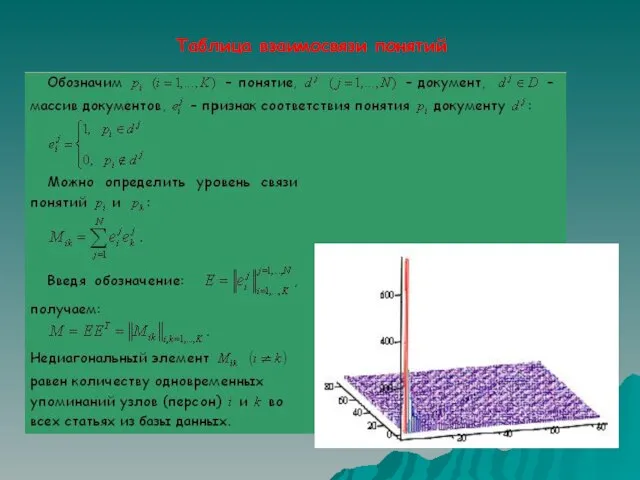
Слайд 5Коэффициент сцепления
Коэффициент сцепления

Слайд 6Неявные связи (матрица скрытности)
Неявные связи (матрица скрытности)
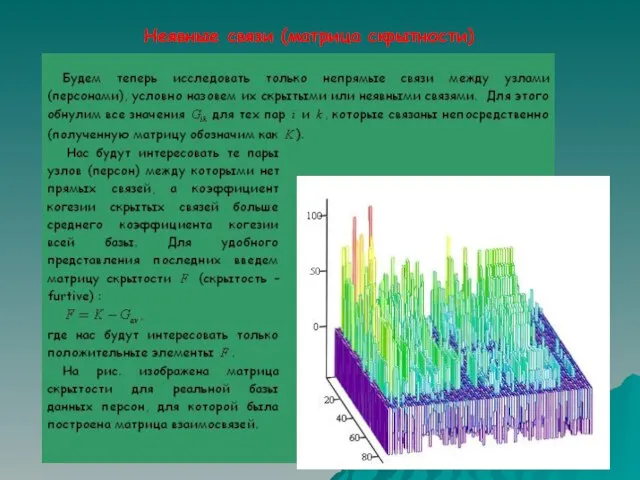
Слайд 7Скрытые связи слов
Слова считаются связанными, если они стоят рядом с текстом.
Известно,
Скрытые связи слов
Слова считаются связанными, если они стоят рядом с текстом.
Известно,
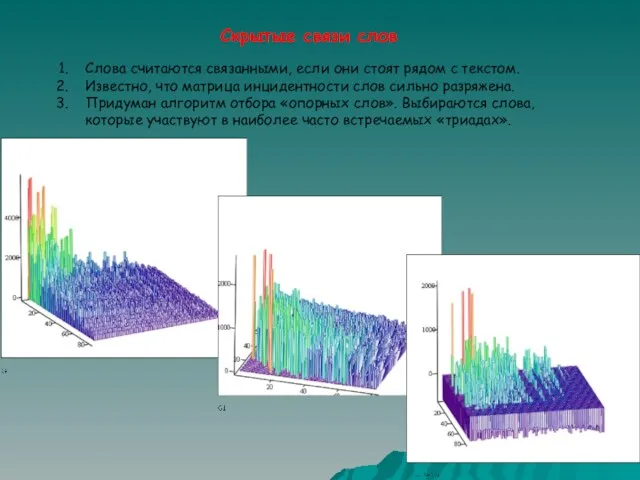
Придуман алгоритм отбора «опорных слов». Выбираются слова, которые участвуют в наиболее часто встречаемых «триадах».
Слайд 8Некоторые выводы
Приведенный метод во многом напоминает подходы, базирующиеся на комбинаторном кластерном анализе,
Некоторые выводы
Приведенный метод во многом напоминает подходы, базирующиеся на комбинаторном кластерном анализе,

В отличие от существующих в настоящее время подходов к выявлению взаимосвязей понятий, предложенный метод позволяет выявлять, определять относительный вес и визуализировать неявные связи любых уровней.
Вместе с тем рассмотренное направление анализа сложных сетей сегодня актуально в маркетинговых и социальных исследованиях, в конкурентной разведке, в задачах выявления и визуализации различных сообществ.
 Презентация на тему ТАМОЖЕННАЯ ПРОЦЕДУРА РЕИМПОРТА
Презентация на тему ТАМОЖЕННАЯ ПРОЦЕДУРА РЕИМПОРТА  Chasodei gazetа (1)
Chasodei gazetа (1) Загрязнение продуктов питания
Загрязнение продуктов питания МОБИЛЬНЫЙ ЖЕЛЕЗНОДОРОЖНЫЙ КОМПЛЕКС ЭЛЕКТРОСНАБЖЕНИЯ (МЖКЭС)
МОБИЛЬНЫЙ ЖЕЛЕЗНОДОРОЖНЫЙ КОМПЛЕКС ЭЛЕКТРОСНАБЖЕНИЯ (МЖКЭС) ОСОБЕННОСТИ ПРЕДМЕТА «ОСНОВЫ РЕЛИГИОЗНЫХ КУЛЬТУР И СВЕТСКОЙ ЭТИКИ»
ОСОБЕННОСТИ ПРЕДМЕТА «ОСНОВЫ РЕЛИГИОЗНЫХ КУЛЬТУР И СВЕТСКОЙ ЭТИКИ» Задание 4
Задание 4 Spotlight - 3
Spotlight - 3 С. Михалков – детям Басня «Ошибка»
С. Михалков – детям Басня «Ошибка» По страницам школьной жизни…
По страницам школьной жизни… Владимирская гладь мли Верхошов
Владимирская гладь мли Верхошов Виды тропов и стилистических фигур
Виды тропов и стилистических фигур ДЗ
ДЗ Стандарты второго поколения ФГОС
Стандарты второго поколения ФГОС Зразок оформлення ВКО
Зразок оформлення ВКО Тектономагнитный метод мониторинга напряженного состояния земной коры и его использование в Байкальском регионе и на Алтае.
Тектономагнитный метод мониторинга напряженного состояния земной коры и его использование в Байкальском регионе и на Алтае. Направление подготовки Гостиничное дело
Направление подготовки Гостиничное дело Отчет о проведении проекта Ты - оратор
Отчет о проведении проекта Ты - оратор Ata
Ata Кустарниковый пожар, ситуация - выживание
Кустарниковый пожар, ситуация - выживание Цель урока: Познакомить со стилями. Развивать творческое мышление, самостоятельность. Задачи: создать условия для развития у обуча
Цель урока: Познакомить со стилями. Развивать творческое мышление, самостоятельность. Задачи: создать условия для развития у обуча Дневник достижений ученика начальной школы как одна из систем оценки достижений учащихся
Дневник достижений ученика начальной школы как одна из систем оценки достижений учащихся first toys
first toys Кривые
Кривые СТИЛИСТ-ИМИДЖМЕЙКЕР_ БАЗА
СТИЛИСТ-ИМИДЖМЕЙКЕР_ БАЗА Культура и искусство
Культура и искусство Тема урока «Учимся видеть и писать разделительный мягкий знак в словах»
Тема урока «Учимся видеть и писать разделительный мягкий знак в словах» Этиология, патогинез
Этиология, патогинез  Магистратура Государственное управление и публичная политика. График сдачи работ магистерской диссертации
Магистратура Государственное управление и публичная политика. График сдачи работ магистерской диссертации