Слайд 2О методе
Приведенный метод решения неравенств позволяет решать их более компактно, а потому

быстрее, что особенно актуально сейчас, когда в задании С3 в ЕГЭ необходимо решить неравенство повышенного уровня сложности.
Представленный метод позволяет свести решение сложного, громоздкого неравенства к классическому (школьному) методу интервалов для многочленов.
Слайд 3ТЕОРИЯ
Рассматриваемые методы решения достаточно эффективны при решении неравенств, левая часть которых представляет

собой произведение (частное) двух функций указанных ниже видов, а правая часть равна нулю.
Традиционные решения таких неравенств путем рассмотрения двух случаев (или применение обобщенного метода интервалов) оказываются более громоздкими по сравнению с методом замены функции.
Слайд 4УТВЕРЖДЕНИЕ
Если область определения, нули и промежутки знакопостоянства функции соответственно совпадают с областью

определения, нулями и промежутками знакопостоянства функции ,
то неравенства:
равносильны.
Слайд 5Что это значит практически?
Утверждение означает то, что если одна из функций или

имеет более простой вид, то при решении неравенств указанного выше вида ее можно «заменить» на другую.
Рассмотрим основные примеры таких пар функций.
Слайд 6Показательные неравенства
1. Функции

Слайд 10Неравенства с модулем
2. Функции
Действительно, имеем:

Слайд 12Иррациональные неравенства
3.Функции

Слайд 13Действительно, имеем:
Следовательно, при четном n для функций и также выполнены
условия

утверждения.
Слайд 15Логарифмические неравенства
4. Функции

Слайд 16Действительно, очевидно, что области определения этих функций совпадают. Кроме того, при а>1

имеем:


















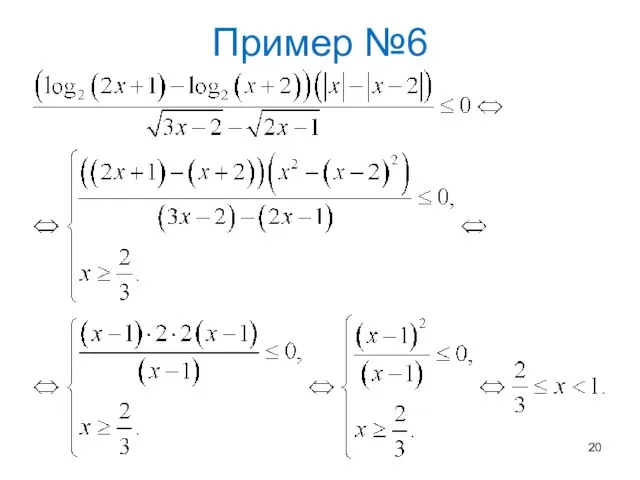






 Инфраструктурные инвестиции
Инфраструктурные инвестиции Културен туризъм: международен маркетинг Бележки към кръглата маса организирана от ПП ГЕРБ Асеновград, 23.06.09
Културен туризъм: международен маркетинг Бележки към кръглата маса организирана от ПП ГЕРБ Асеновград, 23.06.09 Pos материалы гербион
Pos материалы гербион Презентация на тему Неофициальные символы России
Презентация на тему Неофициальные символы России CPA launches FOD
CPA launches FOD Методы и приборы разрушающего контроля, применяемые при обследовании
Методы и приборы разрушающего контроля, применяемые при обследовании ЖИЗНЬ И БЫТ В СРЕДНЕВЕКОВОМ ЗАМКЕ
ЖИЗНЬ И БЫТ В СРЕДНЕВЕКОВОМ ЗАМКЕ Презентация компании MOST Marketing«Франчайзинговый пакет: как разработать,чтобы привлечь франчайзи»
Презентация компании MOST Marketing«Франчайзинговый пакет: как разработать,чтобы привлечь франчайзи» Колористика при окрашивании волос. Тест
Колористика при окрашивании волос. Тест Предложение по летнему корпоративному отдыху на стадионе «Труд» (пос. «Старая Купавна»)
Предложение по летнему корпоративному отдыху на стадионе «Труд» (пос. «Старая Купавна») Греческая вазопись
Греческая вазопись Холод в нефтянной промышленности
Холод в нефтянной промышленности Урок-путешествие по разделу «Были-небылицы». Оценка достижений
Урок-путешествие по разделу «Были-небылицы». Оценка достижений LobbyWorks
LobbyWorks Самоиндукция
Самоиндукция Correct сommunication. Правильное общение
Correct сommunication. Правильное общение Тема: «Положение человека в системе животного мира. Эволюция гоминид».
Тема: «Положение человека в системе животного мира. Эволюция гоминид». Презентация на тему Выживание в природных условиях после аварии
Презентация на тему Выживание в природных условиях после аварии  ангелы
ангелы Интеллектуально-познавательная игра
Интеллектуально-познавательная игра Анализ применимости ПИК «СтОФ» для массовой оценки стоимости движимого имущества Тевелева Оксана Валерьевна тел: (499) 724-15-14, 8(903)208-
Анализ применимости ПИК «СтОФ» для массовой оценки стоимости движимого имущества Тевелева Оксана Валерьевна тел: (499) 724-15-14, 8(903)208- Fruit and vegetables
Fruit and vegetables Ты подвиг совершил во имя жизни на земле
Ты подвиг совершил во имя жизни на земле Обязательства из односторонних сделок и из действий в чужом интересе. Обязательства из договоров, не подлежащие судебной защите
Обязательства из односторонних сделок и из действий в чужом интересе. Обязательства из договоров, не подлежащие судебной защите ТВ - тюнеры
ТВ - тюнеры Применение программного комплекса CorPos (FORCE Technology Norway AS) для диагностики и прогнозирования коррозии на внутренних стенках газопров
Применение программного комплекса CorPos (FORCE Technology Norway AS) для диагностики и прогнозирования коррозии на внутренних стенках газопров Евгений Замятин
Евгений Замятин Characteristic of grain mass
Characteristic of grain mass