МЕТОДОЛОГИЧЕСКИЕ ПРИНЦИПЫ МИКРОЭКОНОМИЧЕСКОГО АНАЛИЗА

Раздел 1. Тема 3.
Потребительский выбор: анализ процесса принятия решения
(Вэриан, гл. 5;
П&Р, гл. 3)

Раздел 1. Тема 3. Вопросы:
Модель поведения и оптимум потребителя
Графическое решение задачи потребителя
Потребительский спрос

Модель поведения и оптимум потребителя
Тема 3. Вопрос 1.

3.1. Модель поведения и оптимум потребителя
В общем виде модель записывается так (А):
max U(z1, z2,…zn)
B – p1z1 – p2z2 – … – pnzn ≥ 0
z i ≥ 0, i = 1,2,…n

3.1. Модель поведения и оптимум потребителя
Модель для стандартных предпочтений (классическая оптимизационная задача) (В):
max U(z1, z2,…zn)
B – p1z1 – p2z2 – … – pnzn = 0
z i > 0, i = 1,2,…n

3.1. Модель поведения и оптимум потребителя
Универсальным методом решения задачи потребителя является метод неопределенных множителей Лагранжа
Лагранжиан (функция Лагранжа) имеет вид: L(z1, z2,…zn, λ) = U(z1, z2,…zn) +
+ λ(B – p1z1 – p2z2 – … – pnzn), где λ ≥ 0
Максимизируем функцию Лагранжа:
L(z1, z2,…zn, λ) → max

3.1. Модель поведения и оптимум потребителя
В задаче потребителя – только одно ограничение (по расходам)
Ограниченный ресурс – доход (бюджет)
Тогда λ* – оптимальная оценка дохода
Экономический смысл неопределенного множителя Лагранжа в задаче на максимум полезности – предельная полезность дохода (денег)

3.1. Модель поведения и оптимум потребителя

3.1. Модель поведения и оптимум потребителя
Первые n уравнений имеют вид:
(С)

3.1. Модель поведения и оптимум потребителя
Для стандартных предпочтений: zi > 0 Тогда из первых n уравнений получаем:
MU1(z1*, z2*,…zn*)/p1 = MU2(z1*, 2*,…zn*)/p2 =
= … = MUn(z1*, z2*,…zn*)/pn = λ*
В оптимальном наборе предельные полезности благ, соотнесенные с ценами, (взвешенные предельные полезности благ) равны

3.1. Модель поведения и оптимум потребителя
Равенство взвешенных предельных полезностей принято называть «условием оптимальности потребительского набора»
Это условие выполняется только в случае «внутреннего оптимума» (все zi* > 0)
Также оно известно как эквимаржинальный принцип

3.1. Модель поведения и оптимум потребителя
Рассмотрим решение задачи потребителя в формулировке (А), в которой представлены:
ограничения на неотрицательность компонентов потребительского набора
ограничение по расходам сформулировано в виде нестрогого неравенства

3.1. Модель поведения и оптимум потребителя
В представленной формулировке задачи потребителя необходимое условие достижения Лагранжианом экстремума (F.O.C.) – неположительность первых n частных производных и неотрицательность производной по λ
Для решения используется совокупность условий, известных как условия Куна-Такера (Kuhn-Tucker conditions) (1) – (6)

3.1. Модель поведения и оптимум потребителя

3.1. Модель поведения и оптимум потребителя

3.1. Модель поведения и оптимум потребителя
Из первых 2n уравнений [(1), (2)] в результате преобразований можно получить систему (D):
(D)

3.1. Модель поведения и оптимум потребителя
Из системы (D) получим условия (Е):

3.1. Модель поведения и оптимум потребителя
Из (4) и (5) получим (F):
(F)

3.1. Модель поведения и оптимум потребителя
Условия (Е) и (F) называются условиями дополняющей нежесткости
Если MUk(z1*, z2*,…zn*)/pk < λ ⇒ zk* = 0 (из условий дополняющей нежесткости
Экономический смысл:

Графическое решение задачи потребителя
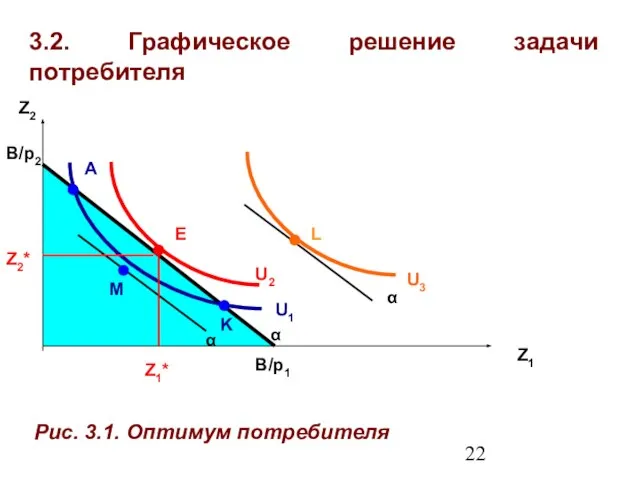
Тема 3. Вопрос 2.

3.2. Графическое решение задачи потребителя
Z1
Z2
U3
U2
U1
L
E
M
A
α
α
B/p1
B/p2
Рис. 3.1. Оптимум потребителя
α
K
Z2*
Z1*

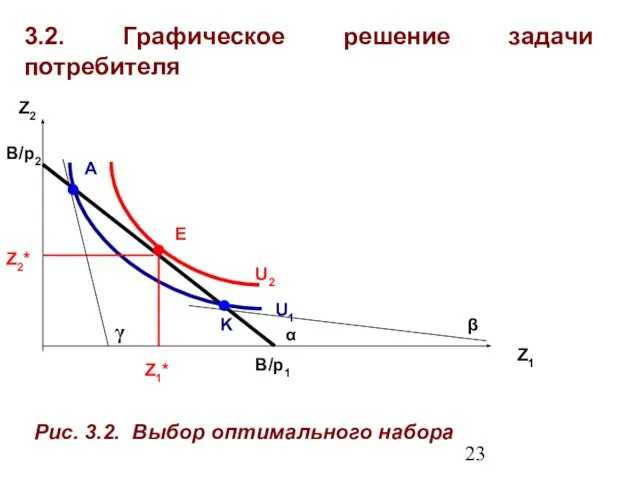
3.2. Графическое решение задачи потребителя
Z1
Z2
U2
U1
E
A
B/p1
B/p2
Рис. 3.2. Выбор оптимального набора
β
K
Z2*
Z1*
α
γ

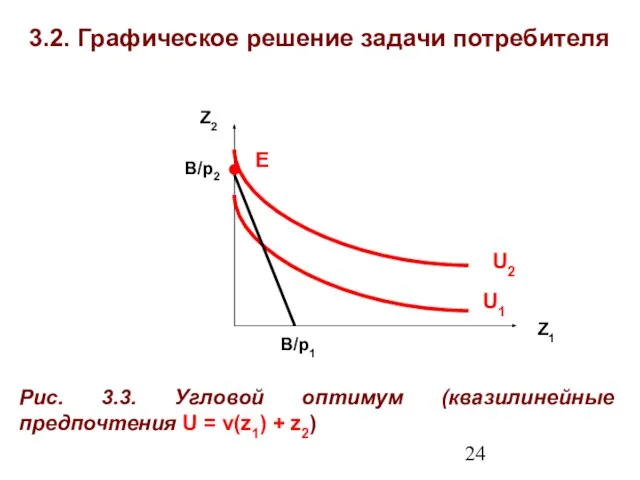
3.2. Графическое решение задачи потребителя
Z1
Z2
Рис. 3.3. Угловой оптимум (квазилинейные предпочтения U = v(z1) + z2)
U1
U2
B/p1
B/p2
Е

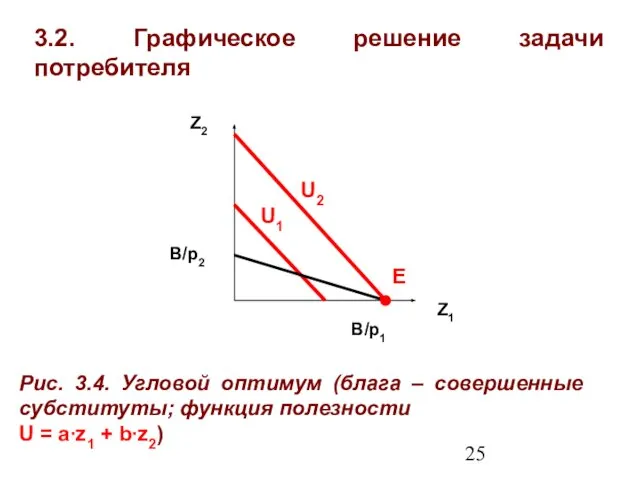
3.2. Графическое решение задачи потребителя
Z1
Z2
Рис. 3.4. Угловой оптимум (блага – совершенные субституты; функция полезности
U = a∙z1 + b∙z2)
U1
U2
B/p1
B/p2
Е

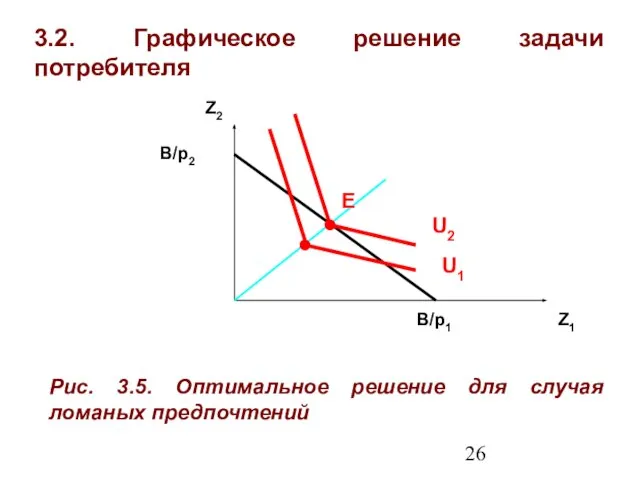
3.2. Графическое решение задачи потребителя
Z1
Z2
Рис. 3.5. Оптимальное решение для случая ломаных предпочтений
U2
U1
B/p1
B/p2
Е

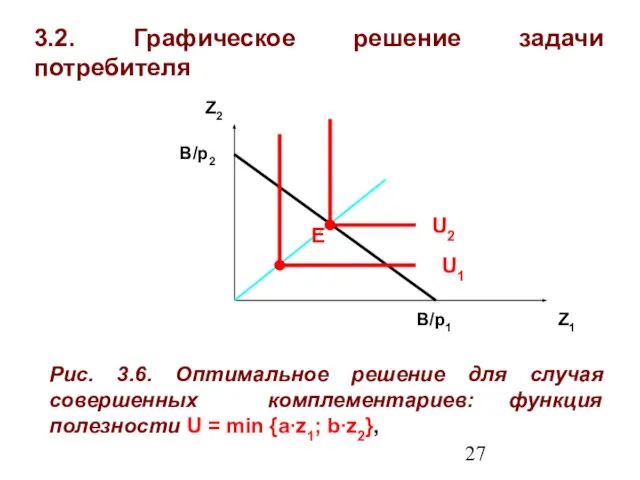
3.2. Графическое решение задачи потребителя
Z1
Z2
Рис. 3.6. Оптимальное решение для случая совершенных комплементариев: функция полезности U = min {a∙z1; b∙z2},
U2
U1
B/p1
B/p2
Е

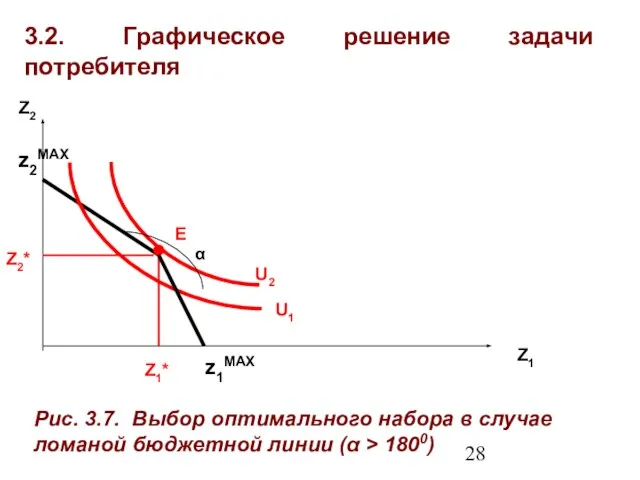
3.2. Графическое решение задачи потребителя
Z1
Z2
U2
U1
E
z1MAX
Рис. 3.7. Выбор оптимального набора в случае ломаной бюджетной линии (α > 1800)
Z2*
Z1*
α
z2MAX

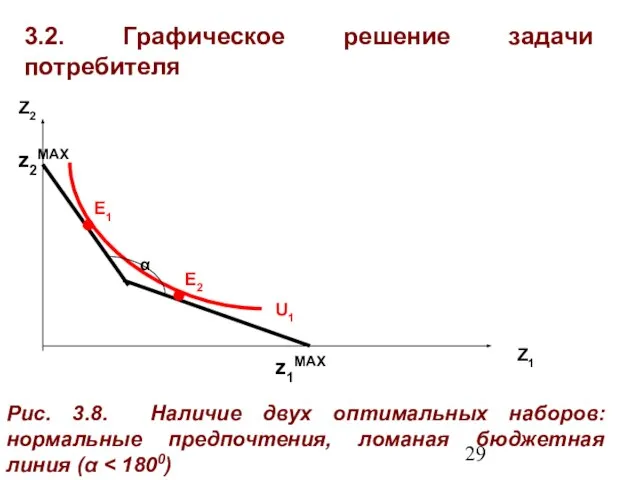
3.2. Графическое решение задачи потребителя
Z1
Z2
E2
U1
z1MAX
Рис. 3.8. Наличие двух оптимальных наборов: нормальные предпочтения, ломаная бюджетная линия (α < 1800)
α
z2MAX
E1

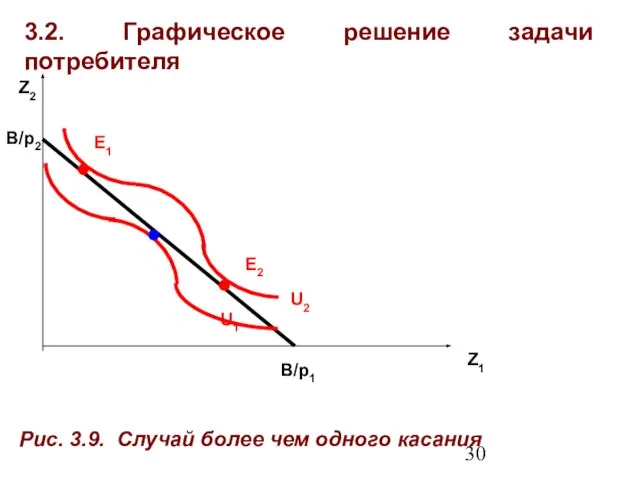
3.2. Графическое решение задачи потребителя
Z1
Z2
E2
U2
Рис. 3.9. Случай более чем одного касания
E1
B/p2
B/p1
U1

Потребительский спрос
Тема 3. Вопрос 3.

3.3. Потребительский спрос
Спрос предъявляется на набор, а не отдельное благо ⇒
Спрос – векторная функция:

3.3. Потребительский спрос
Полагая, что в наборе – только два блага, получим: D1 ≡ z1* = f1(p1,p2,B)
D2 ≡ z2* = f2(p2,p1,B)

3.3. Потребительский спрос
Предпочтения агента таковы: блага – совершенные субституты
Такие предпочтения описываются функцией полезности U = a∙z1 + b∙z2
Соотношение a/b может быть любым:
a/b = 1
a/b > 1
a/b < 1
Решение потребителя будет зависеть от соотношения a/b = |MRS21|, а также от соотношения цен p1/p2

3.3. Потребительский спрос
Возможны три случая:
a/b > p1/p2 ⇒ a/p1 > b/p2 ⇒ угловое решение: D1 ≡ z1* = B/p1; D2 ≡ z2* = 0 (см. рис. 3.10.)
a/b < p1/p2 ⇒ a/p1 < b/p2 ⇒ угловое решение: D2 ≡ z2* = B/p2; D1 ≡ z1* = 0
a/b = p1/p2 ⇒ a/p1 = b/p2 (для любого набора) ⇒
0 ≤ D1 ≡ z1* ≤ B/p1
B/p2 ≥ D2 ≡ z2* ≥ 0

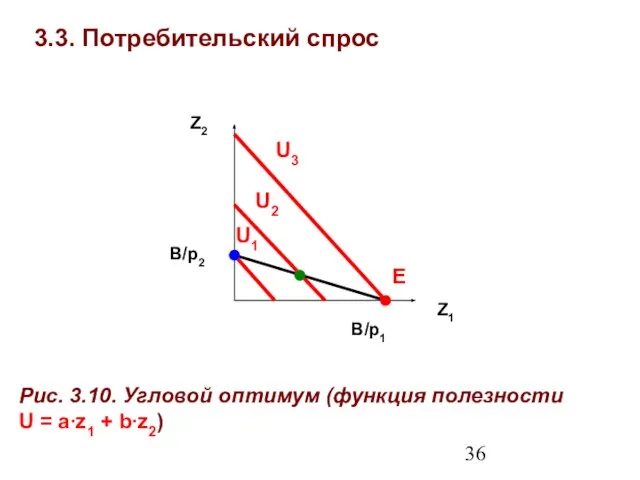
3.3. Потребительский спрос
Z1
Z2
Рис. 3.10. Угловой оптимум (функция полезности
U = a∙z1 + b∙z2)
U1
U2
B/p1
B/p2
Е
U3

3.3. Потребительский спрос
Итак, решение агента будет угловым, если |MRS21| ≠ p1/p2 Будут иметь место множественные решения агента о составе набора, если |MRS21| = p1/p2
Тогда спрос, например, на первое благо:
B/p1, if p1 < (a/b)p2
D1 = 0, if p1 > (a/b)p2
∈ [0; B/p1], if p1 = (a/b)p2

3.3. Потребительский спрос
Рассмотрим предпочтения, описываемые функцией полезности Леонтьевского типа (блага –совершенные комплементарии):
U = min {a∙z1; b∙z2}
В этом случае оптимальный набор всегда лежит на луче с наклоном α:
tg α = a/b
Оптимальный набор представлен на рис. 3.11.

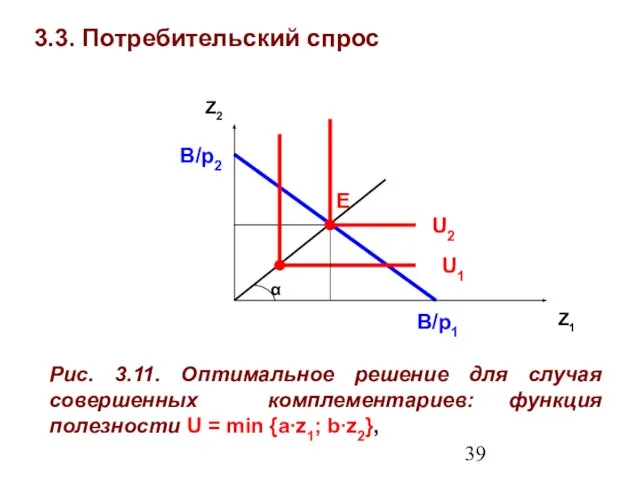
3.3. Потребительский спрос
Z1
Z2
Рис. 3.11. Оптимальное решение для случая совершенных комплементариев: функция полезности U = min {a∙z1; b∙z2},
U2
U1
B/p1
B/p2
Е
α

3.3. Потребительский спрос
Состав оптимального набора из благ-комплементариев определяется с учетом «технологии потребления»:
z2* = (a/b)z1*
Тогда из решения задачи потребителя получим:
D1 ≡ z1* = b∙B/[b∙p1 + a∙p2]
D2 ≡ z2* = a∙B/[b∙p1 + a∙p2]

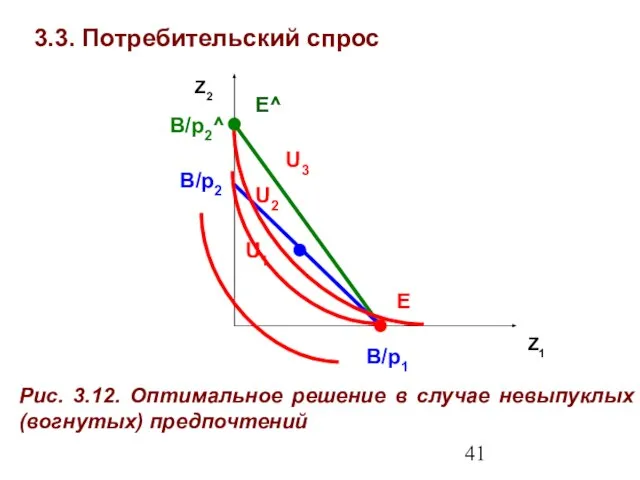
3.3. Потребительский спрос
Z1
Z2
Рис. 3.12. Оптимальное решение в случае невыпуклых (вогнутых) предпочтений
E
В/p1
Е^
U1
U2
В/p2
U3
В/p2^

3.3. Потребительский спрос
В случае стандартных предпочтений, описываемых функцией полезности Кобба-Дугласа: U = z1az2b
См. рис. 3.1.
Всегда – внутренний оптимум:
D1 ≡ z1* = a∙B/[(a + b)∙p1]
D2 ≡ z2* = b∙B/[(a + b)∙p2]

3.3. Потребительский спрос
Стандартные предпочтения, определенные на множестве наборов Rn+
Описываются функцией полезности Кобба-Дугласа:

3.3. Потребительский спрос
Для стандартных предпочтений функции спроса на i-е благо будут иметь вид:
(1)

3.3. Потребительский спрос
Все рассмотренные функции спроса получены из решения задачи на максимум полезности при ограничении на расходы
Это – функции спроса по Маршаллу (маршаллианские/маршалловские функции спроса)

Раздел 1. Тема 4.
Поведение потребителя в условиях изменяющихся дохода и цен
(Вэриан, гл. 6, 8, 9, 14;
П&Р, гл. 3)

Спрос как функция дохода
Cпрос как функция цены
Влияние на выбор потребителя изменений в относительных ценах: эффект дохода и эффект замещения
Выбор потребителя при натуральном доходе
Оценка изменений в благосостоянии потребителя
Тема 4. Вопросы:

Спрос как функция дохода
Тема 4. Вопрос 1.

4.1. Спрос как функция дохода. Линия «доход – потребление» и функции Энгеля Логика анализа: изменение дохода → изменение состава оптимального набора → изменение спроса
При этом полагаем: P = const (принцип «при прочих равных условиях») ⇒ изменения в спросе обусловливаются только изменениями дохода

4.1. Спрос как функция дохода. Линия «доход – потребление» и функции Энгеля
Для нормальных благ, по которым насыщение не наступает:

4.1. Спрос как функция дохода. Линия «доход – потребление» и функции Энгеля
Для нормальных благ, по которым насыщение возможно:
Для товаров, потребляемых в строго определенном объеме:

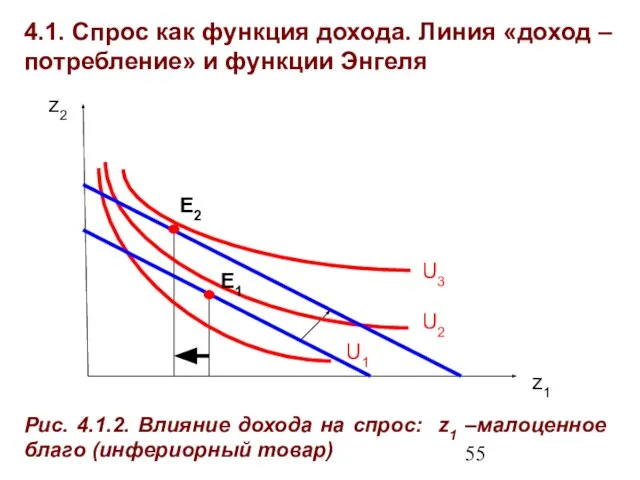
4.1. Спрос как функция дохода. Линия «доход – потребление» и функции Энгеля
Для малоценных благ (инфериорных товаров, товаров низшей категории):

4.1. Спрос как функция дохода. Линия «доход – потребление» и функции Энгеля
Z1
B1/p1
B2/p1
B2/p2
B1/p2
U2
U1
E1
E2
линия «доход - потребление»
Рис. 4.1.1. Влияние дохода на спрос и линия «доход-потребление» для случая стандартных предпочтений
Z2

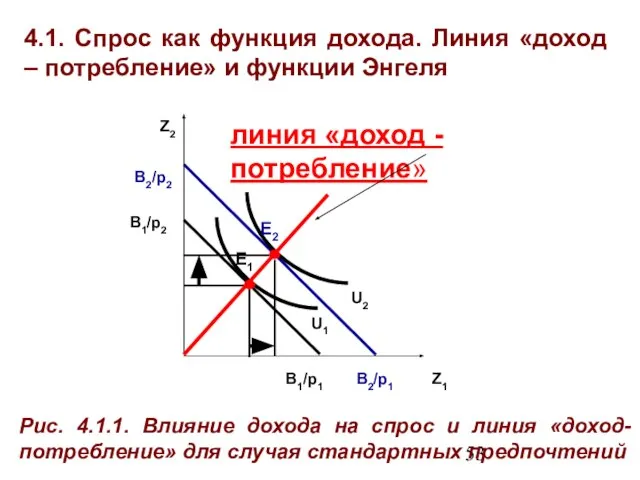
4.1. Спрос как функция дохода. Линия «доход – потребление» и функции Энгеля Линия «доход - потребление» – совокупность оптимальных наборов, формируемых при неизменных ценах и изменяющемся доходе
Другое название: «траектория расширения дохода»

4.1. Спрос как функция дохода. Линия «доход – потребление» и функции Энгеля
Рис. 4.1.2. Влияние дохода на спрос: z1 –малоценное благо (инфериорный товар)
z1
z2
U3
U2
U1
E1
E2

4.1. Спрос как функция дохода. Линия «доход – потребление» и функции Энгеля Анализ линии «доход-потребление» позволяет построить функции потребления от дохода – функции Энгеля
Функции Энгеля:
z1* = f1(B); z2* = f2(B)

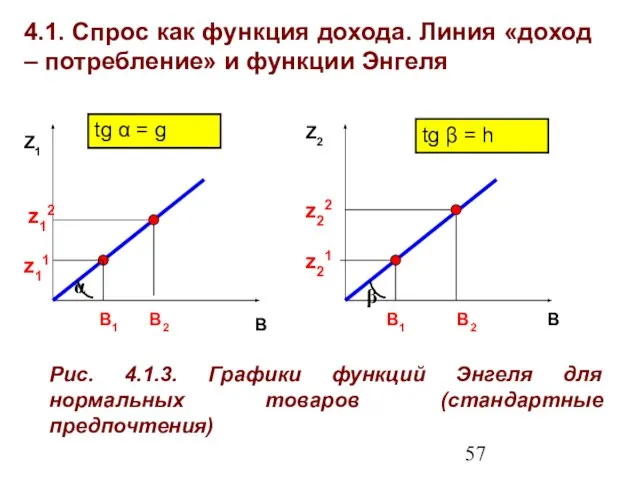
4.1. Спрос как функция дохода. Линия «доход – потребление» и функции Энгеля
Z1
Z2
Рис. 4.1.3. Графики функций Энгеля для нормальных товаров (стандартные предпочтения)
z11
В
В
z12
z21
z22
В2
В1
В1
В2
tg α = g
α
β
tg β = h

4.1. Спрос как функция дохода. Линия «доход – потребление» и функции Энгеля Формализованное представление функций Энгеля для нормальных предпочтений, определенных на наборах из двух благ; функция полезности Кобба-Дугласа: U = z1az2b:
Z1 = aB/[(a+b)p1] = gB, где g = a/[(a+b)p1] = tg α = const
Z2 = bB/[(a+b)p2] = hB, где h = b/[(a+b)p2] = tg β = const (См. рис. 4.1.3.)

4.1. Спрос как функция дохода. Линия «доход – потребление» и функции Энгеля Рассмотрим конфигурацию линии «доход – потребление» для случая предпочтений Леонтьевского типа (см. рис. 4.1.4.): U = min {a∙z1; b∙z2}
Наклон этой линии: tg γ = a/b
На основе линии «доход – потребление» получим функции спроса на z1 и z2

4.1. Спрос как функция дохода. Линия «доход – потребление» и функции Энгеля Функция спроса на первый товар:
Z1 = b∙B/[bp1 + ap2] = g∙B,
где g = tg α на рис. 4.1.3.
Функция спроса на второй товар:
Z2 = a∙B/[bp1 + ap2] = h∙B,
где h = tg β на рис. 4.1.3.

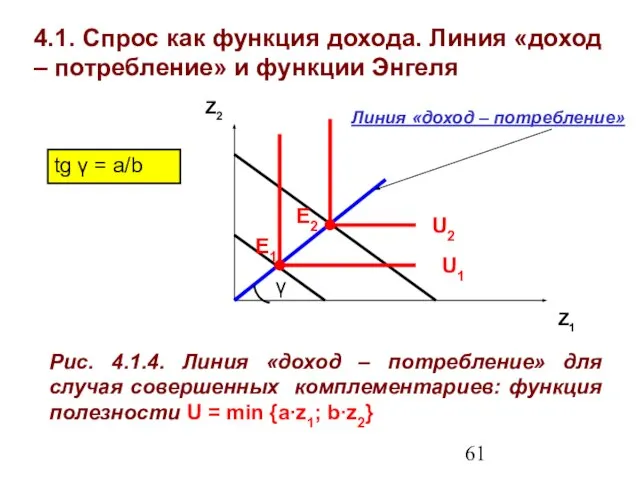
4.1. Спрос как функция дохода. Линия «доход – потребление» и функции Энгеля
Z1
Z2
Рис. 4.1.4. Линия «доход – потребление» для случая совершенных комплементариев: функция полезности U = min {a∙z1; b∙z2}
U2
U1
Е1
Линия «доход – потребление»
Е2
γ
tg γ = a/b

4.1. Спрос как функция дохода. Линия «доход – потребление» и функции Энгеля Рассмотрим случай совершенных субститутов
Предположим a/p1 > b/p2 ⇒ угловое решение: D1 ≡ z1* = B/p1; D2 ≡ z2* = 0
Тогда линия «доход – потребление» – горизонтальная прямая (см. рис. 4.1.5.)
График функции спроса в системе координат «доход – количество Z1»: прямая с положительным наклоном η: tg η = 1/p1

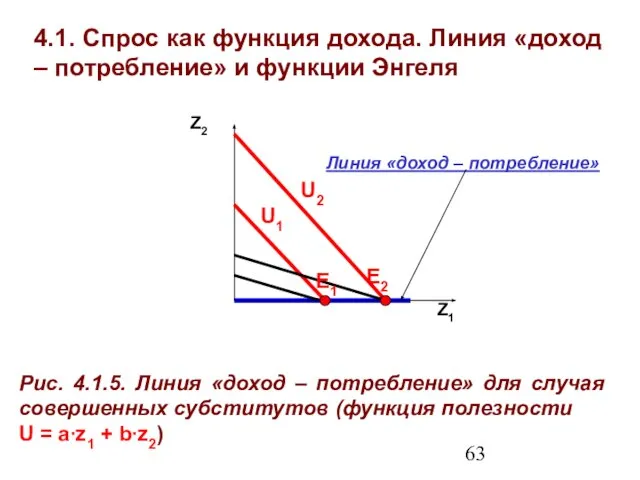
4.1. Спрос как функция дохода. Линия «доход – потребление» и функции Энгеля
Z1
Z2
Рис. 4.1.5. Линия «доход – потребление» для случая совершенных субститутов (функция полезности
U = a∙z1 + b∙z2)
U1
U2
Е1
Линия «доход – потребление»
Е2

4.1. Спрос как функция дохода. Линия «доход – потребление» и функции Энгеля Гомотетичные предпочтения – такие предпочтения, что:
если Y ≻ X, то и αY ≻ αX при любом α > 0
Иначе говоря, потребитель предпочитает наборы с определенной структурой
Структура оптимальных наборов определяется предпочтениями и относительными ценами

4.1. Спрос как функция дохода. Линия «доход – потребление» и функции Энгеля Состав набора изменяется при изменении дохода (бюджета); структура при наборов при этом – неизменна
Если предпочтения потребителя гомотетичны, то линия «доход – потребление» – луч, исходящий из начала координат

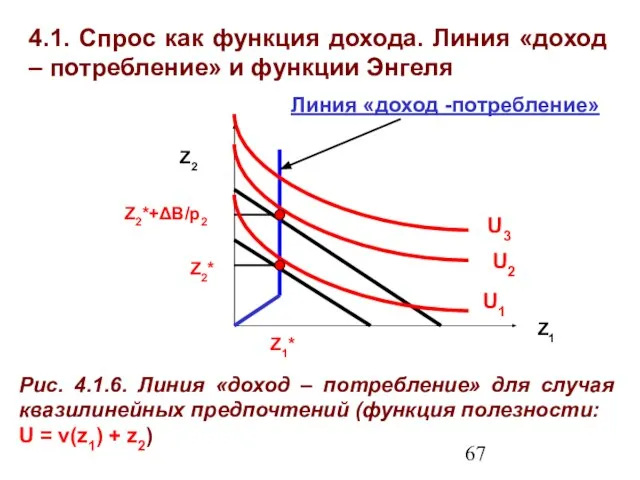
4.1. Спрос как функция дохода. Линия «доход – потребление» и функции Энгеля Квазилинейные предпочтения: особый тип предпочтений, описываются функцией U(z1,z2) = v(z1) + z2
Особый вид имеют и линия «доход – потребление», и функции Энгеля
Пусть исходное решение принято при бюджете В0 и ценах (p1,p2) ⇒ состав оптимального набора Е1: (z1*,z2*)
Осуществим сдвиг БЛ вправо: В0+ΔВ ⇒ состав оптимального набора Е2: (z1*,z2*+k), где k = ΔВ/p2

4.1. Спрос как функция дохода. Линия «доход – потребление» и функции Энгеля
Z1
Z2
Рис. 4.1.6. Линия «доход – потребление» для случая квазилинейных предпочтений (функция полезности:
U = v(z1) + z2)
U1
U2
U3
Z1*
Z2*
Z2*+ΔB/p2
Линия «доход -потребление»

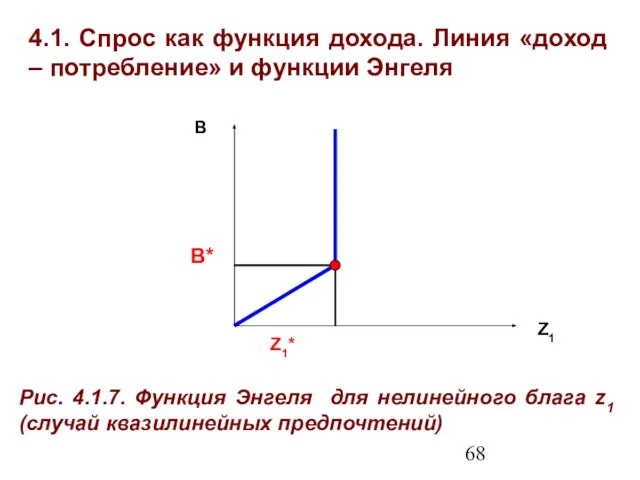
4.1. Спрос как функция дохода. Линия «доход – потребление» и функции Энгеля
Z1
В
Рис. 4.1.7. Функция Энгеля для нелинейного блага z1 (случай квазилинейных предпочтений)
Z1*
В*

Спрос как функция цены
Тема 4. Вопрос 2.

4.2. Спрос как функция цены
Спрос является функцией не только дохода, но и цен благ, включаемых потребителем в оптимальный набор:

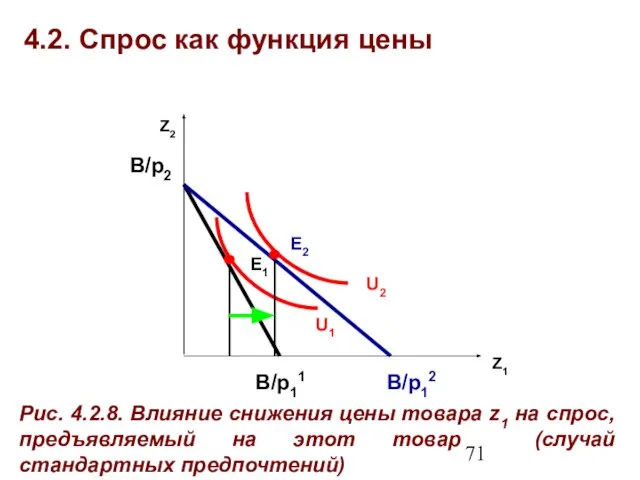
4.2. Спрос как функция цены
Z1
B/p11
B/p12
B/p2
U2
U1
E1
E2
Рис. 4.2.8. Влияние снижения цены товара z1 на спрос, предъявляемый на этот товар (случай стандартных предпочтений)
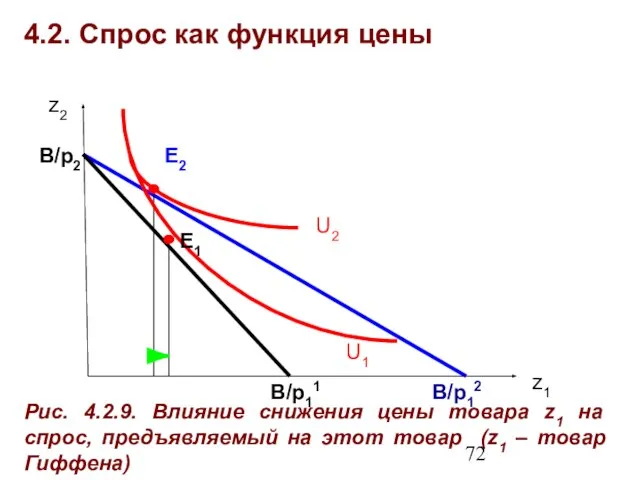
Z2

4.2. Спрос как функция цены
Рис. 4.2.9. Влияние снижения цены товара z1 на спрос, предъявляемый на этот товар (z1 – товар Гиффена)
z1
z2
U2
U1
E1
E2
B/p12
B/p11
B/p2

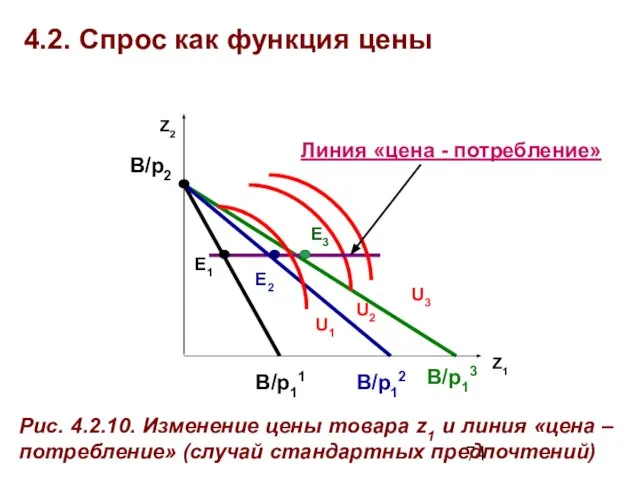
4.2. Спрос как функция цены
Линия «цена – потребление» – совокупность оптимальных наборов, сформированных при различных относительных ценах под воздействием изменения цены одного из товаров
См. рис. 4.2.10.
Конфигурация линии зависит от типа взаимосвязи товаров в потреблении (предпочтений) и может быть любой

4.2. Спрос как функция цены
Z1
B/p11
B/p12
B/p2
U2
U1
E1
E2
Рис. 4.2.10. Изменение цены товара z1 и линия «цена – потребление» (случай стандартных предпочтений)
Z2
E3
U3
B/p13
Линия «цена - потребление»

4.2. Спрос как функция цены
На основе анализа наборов, составляющих линию «цена-потребление», можно получить функции спроса на товары z1 и z2 от цены первого товара при p2 =const B = const:
D1 ≡ z1* = f1(p1;p2;B)
D2 ≡ z2* = f2(p1;p2;B)

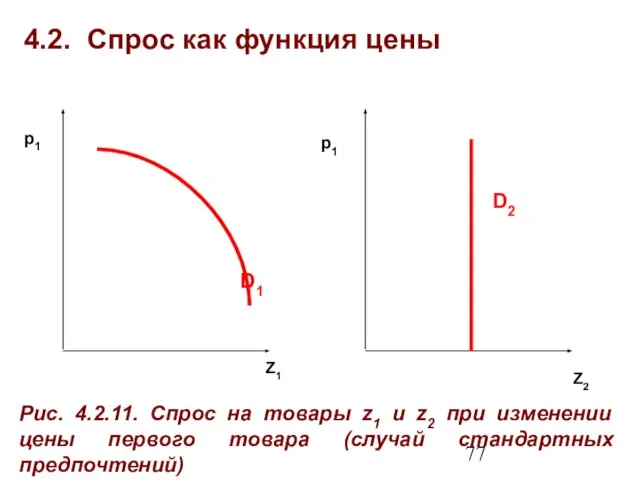
4.2. Спрос как функция цены
Формализованное представление функций спроса от p1 на z1 и z2 для стандартных предпочтений (функция полезности Кобба-Дугласа: U = z1az2b):
Z1(p1) = aB/[(a+b)p1] = k/p1, где k = aB/(a+b)
Z2 (p1) = bB/[(a+b)p2] = const
См. рис. 4.2.11.

4.2. Спрос как функция цены
Z1
Рис. 4.2.11. Спрос на товары z1 и z2 при изменении цены первого товара (случай стандартных предпочтений)
p1
D1
p1
Z2
D2

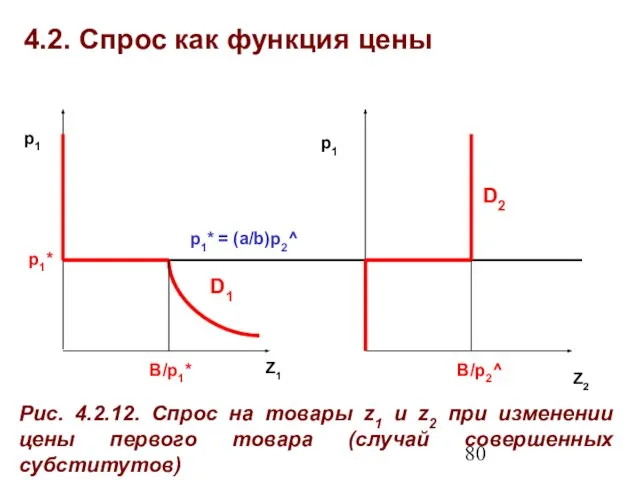
4.2. Спрос как функция цены
Рассмотрим случай совершенных субститутов (аддитивная функция полезности U = az1 + bz2)
При B = const и p2^ = const будем менять цену первого блага ⇒
Спрос на первое благо:
B/p1, if p1 < (a/b)p2^
D1 = 0, if p1 > (a/b)p2^
∈ [0; B/p1], if p1 = (a/b)p2^
См. рис. 4.2.12.

4.2. Спрос как функция цены
При B = const и p2 = const меняем цену первого блага ⇒
Спрос на второе благо:
B/p2, if p1 > (a/b)p2^
D2 = 0, if p1 < (a/b)p2^
∈ [0; B/p1], if p1 = (a/b)p2^
См. рис. 4.2.12.

4.2. Спрос как функция цены
Z1
Рис. 4.2.12. Спрос на товары z1 и z2 при изменении цены первого товара (случай совершенных субститутов)
p1
D1
p1
Z2
D2
p1* = (a/b)p2^
p1*
B/p1*
B/p2^

4.2. Спрос как функция цены
Рассмотрим случай совершенных комплементариев (Леонтьевская функция полезности U = min{az1;bz2}
При B = const и p2^ = const будем менять цену первого блага ⇒
Получим:
D1 ≡ z1* = b∙B/[b∙p1 + a∙p2^]
D2 ≡ z2* = a∙B/[b∙p1 + a∙p2^]
См. рис. 4.2.13.