Содержание
- 2. Економічна раціональність Поведінковий постулат: Індивід, який приймає рішення, завжди обирає товар, якому надає найбільшу перевагу з-поміж
- 3. Споживчий набір Споживчий набір – об’єкт споживчого вибору. Споживчий набір – повний перелік товарів і послуг,
- 4. Споживчий набір Споживчий набір X складається з x1, x2, … хn одиниць товарів і послуг Для
- 5. Уподобання індивіда Порівнюючи 2 різних споживчих набори, А та В: строгі вподобання: А краще, ніж В
- 6. Уподобання індивіда Строгі, слабкі вподобання і байдужість описують всі можливі види вподобань. Зокрема, вони описують порядкові
- 7. Аксіоми про споживчі вподобання Повнота: для будь-яких двох наборів А і В завжди справедливо одне з
- 8. Аксіоми про споживчі вподобання Рефлексивність: будь-який набір А завжди не гірше самого себе, тобто А ≥
- 9. Аксіоми про споживчі вподобання Транзитивність: якщо А віддається перевага над В, і В віддається перевага над
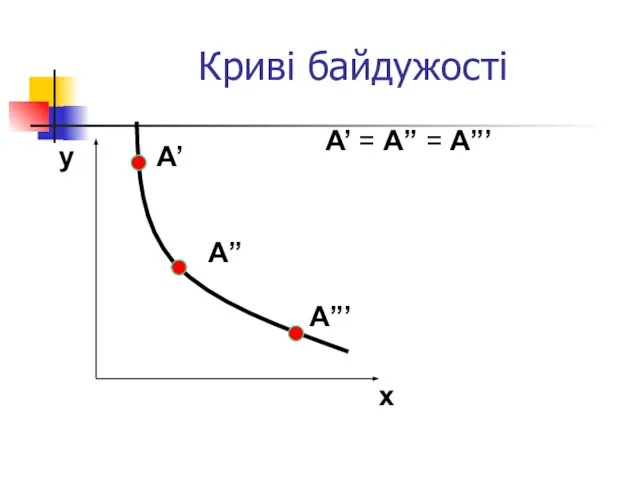
- 10. Криві байдужості Візьмемо набір А’. Множина всіх наборів, яким віддається аналогічна перевага, як А’, називається кривою
- 11. Криві байдужості y x А” А”’ А’ = А” = А”’ А’
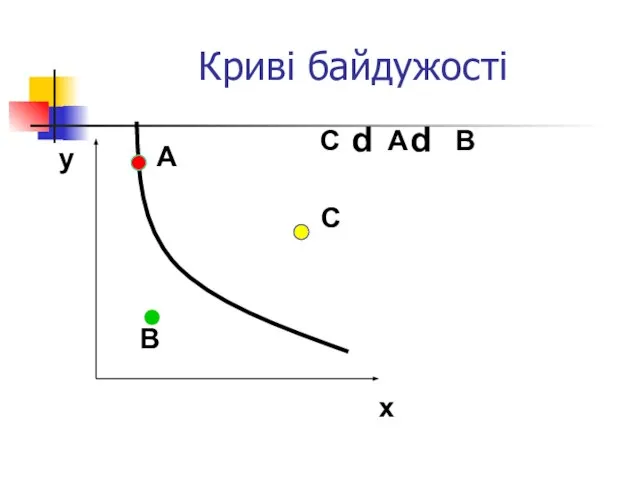
- 12. Криві байдужості y x С А В p p А В С
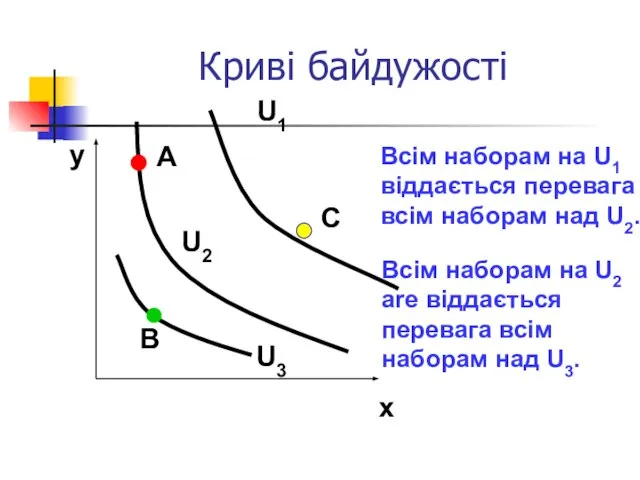
- 13. Криві байдужості y x A Всім наборам на U1 віддається перевага всім наборам над U2. B
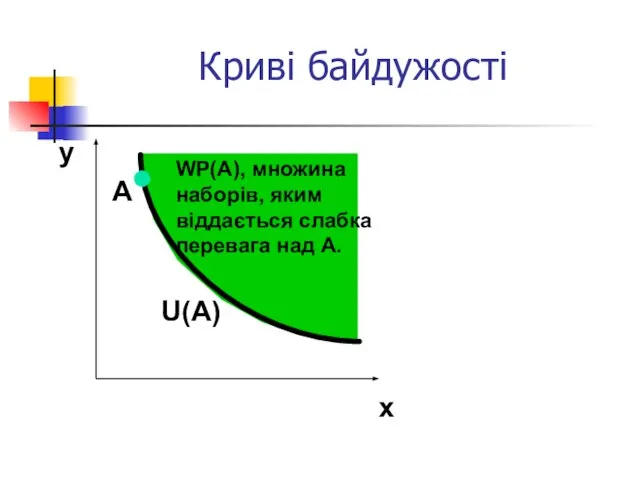
- 14. Криві байдужості y x I(x’) A U(A) WP(A), множина наборів, яким віддається слабка перевага над A.
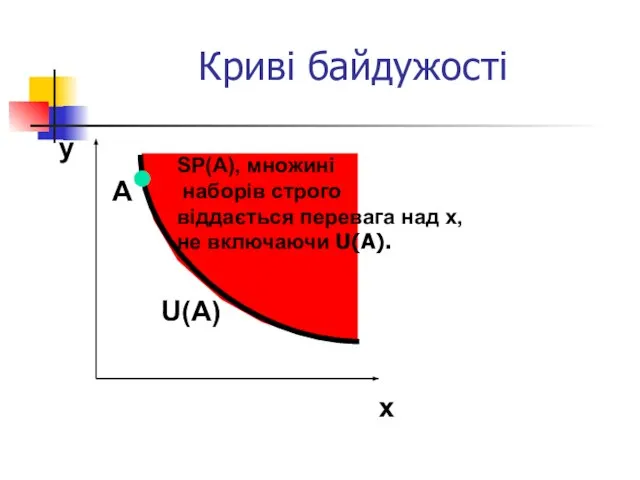
- 15. Криві байдужості y x SP(A), множині наборів строго віддається перевага над x, не включаючи U(A). A
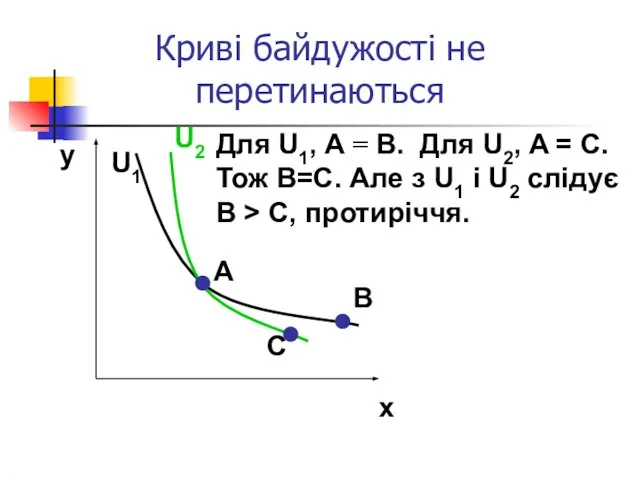
- 16. Криві байдужості не перетинаються y x A B C U1 U2 Для U1, A = B.
- 17. Нахил кривої байдужості Коли більшій кількості товару віддається перевага меншій кількості, товар є благом. Якщо кожен
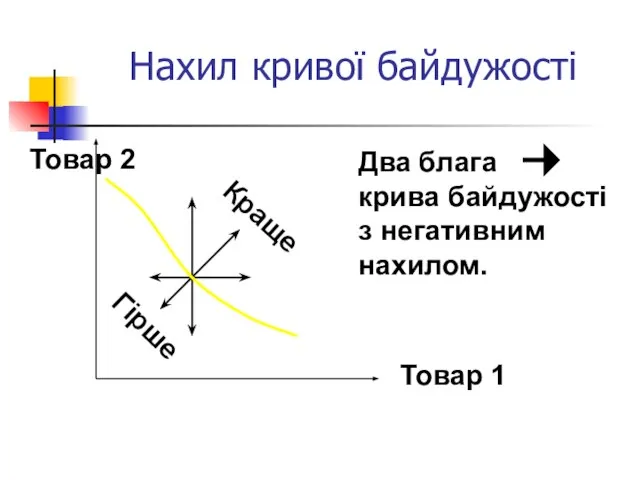
- 18. Нахил кривої байдужості Краще Гірше Товар 2 Товар 1 Два блага крива байдужості з негативним нахилом.
- 19. Нахил кривої байдужості Якщо меншій кількості товару завжди віддається перевага більшій кількості цього товару, він є
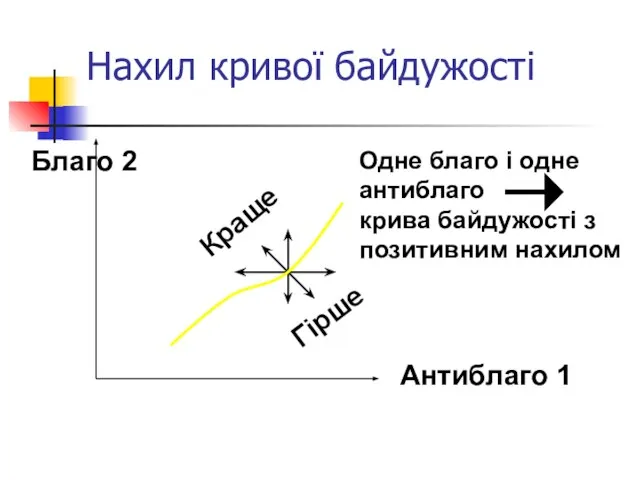
- 20. Нахил кривої байдужості Краще Гірше Благо 2 Антиблаго 1 Одне благо і одне антиблаго крива байдужості
- 21. Нахил кривої байдужості Якщо споживачу байдуже, чи є у нього цей товар, чи ні, товар називається
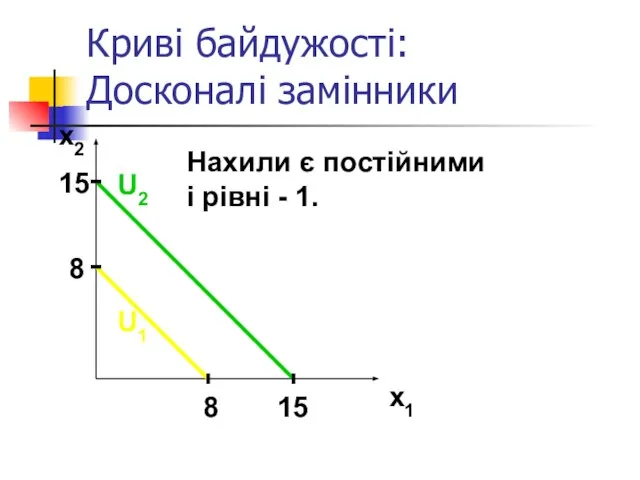
- 22. Криві байдужості: Досконалі замінники Якщо споживач завжди розглядає товари 1 і 2 як еквівалентні, то блага
- 23. Криві байдужості: Досконалі замінники x2 x1 8 8 15 15 Нахили є постійними і рівні -
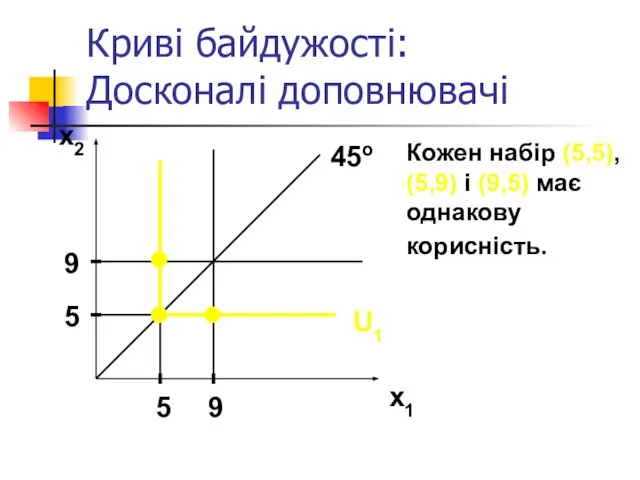
- 24. Криві байдужості: Досконалі доповнювачі Якщо індивід завжди споживає товари 1 і 2 у фіксованій пропорції (наприклад,
- 25. Криві байдужості: Досконалі доповнювачі x2 x1 U1 45o 5 9 5 9 Кожен набір (5,5), (5,9)
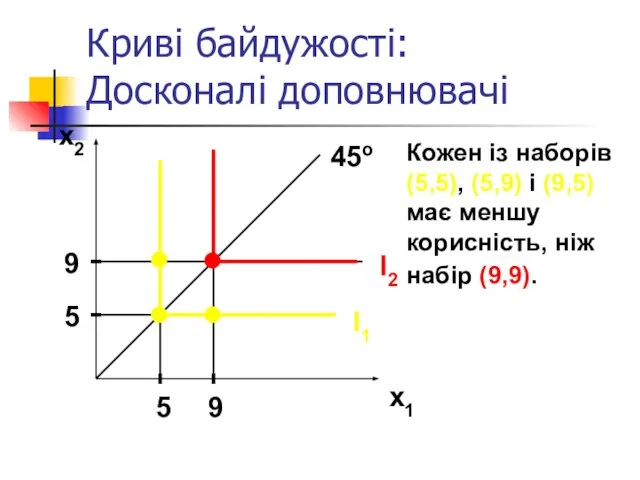
- 26. Криві байдужості: Досконалі доповнювачі x2 x1 I2 I1 45o 5 9 5 9 Кожен із наборів
- 27. Уподобання з точкою насичення Набір, якому строго віддають перевагу над усіма іншими є точкою задоволення або
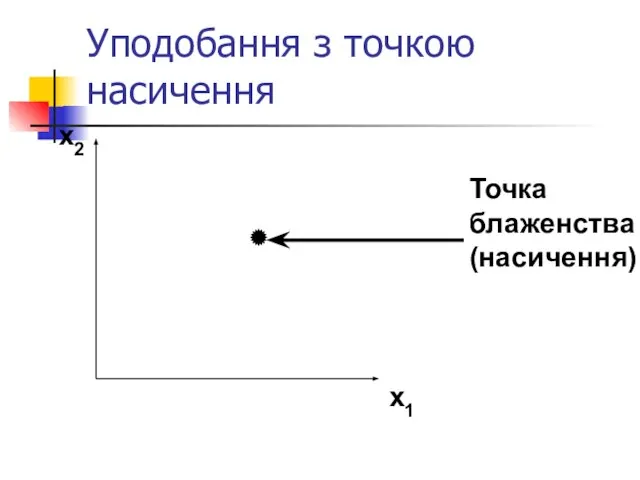
- 28. Уподобання з точкою насичення x2 x1 Точка блаженства (насичення)
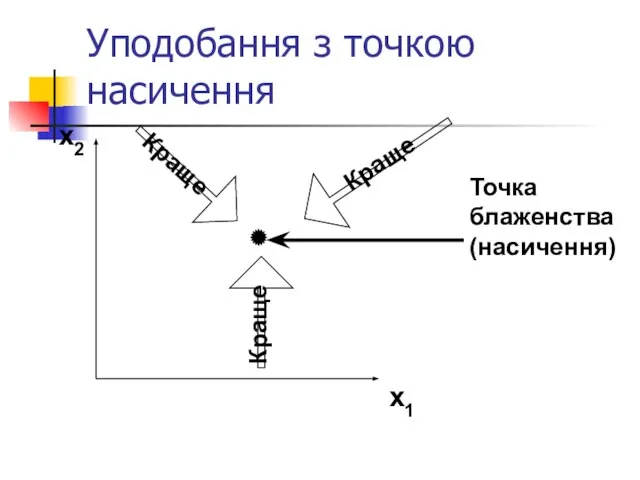
- 29. Уподобання з точкою насичення x2 x1 Краще Краще Краще Точка блаженства (насичення)
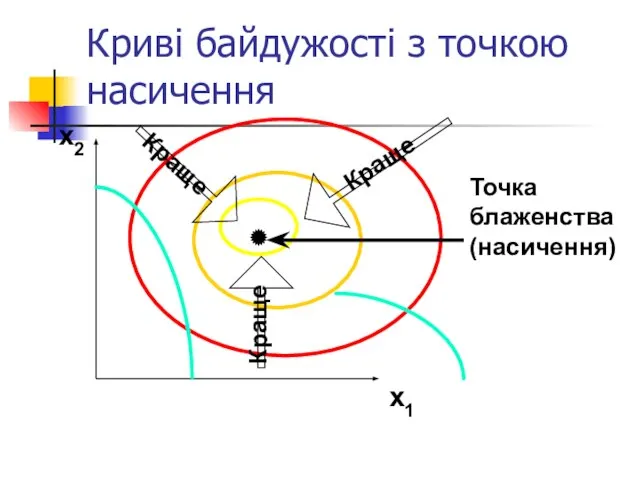
- 30. Криві байдужості з точкою насичення x2 x1 Краще Краще Краще Точка блаженства (насичення)
- 31. Коректні вподобання Відношення щодо вподобань є “коректними”, якщо вони монотонні і випуклі вниз. Монотонність: більшій кількості
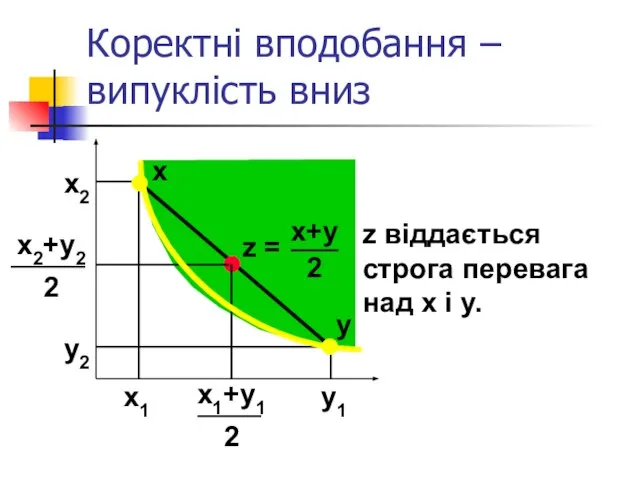
- 32. Коректні вподобання Випуклість вниз: Комбінації наборів віддається перевага над самими наборами. Наприклад, комбінація наборів x і
- 33. Коректні вподобання – випуклість вниз x2 y2 x2+y2 2 x1 y1 x1+y1 2 x y z
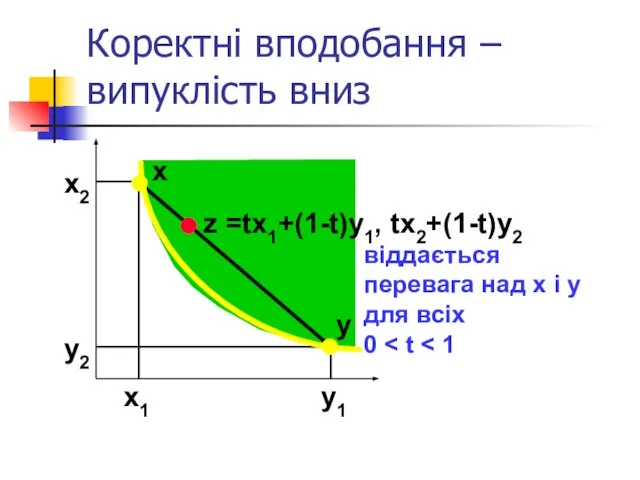
- 34. Коректні вподобання – випуклість вниз x2 y2 x1 y1 x y z =tx1+(1-t)y1, tx2+(1-t)y2 віддається перевага
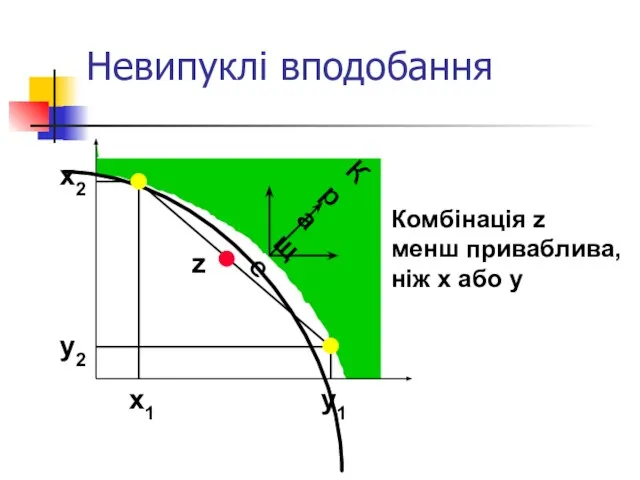
- 35. Невипуклі вподобання x2 y2 x1 y1 z Краще Комбінація z менш приваблива, ніж x або y
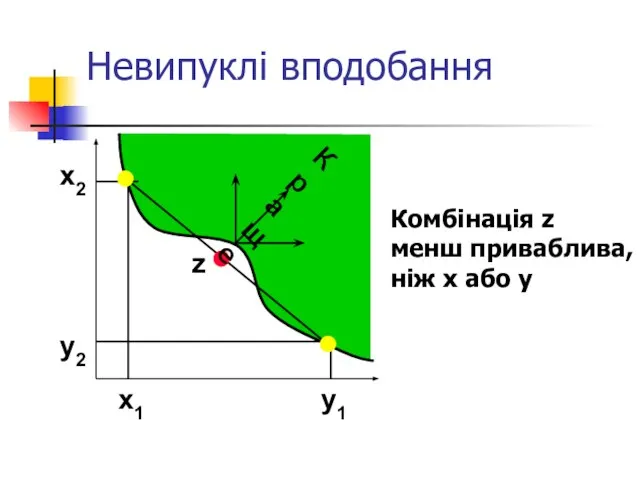
- 36. Невипуклі вподобання x2 y2 x1 y1 z Краще Комбінація z менш приваблива, ніж x або y
- 37. Нахил кривої байдужості Нахил кривої байдужості називається граничною нормою заміщення (MRS). Чи можна визначити MRS?
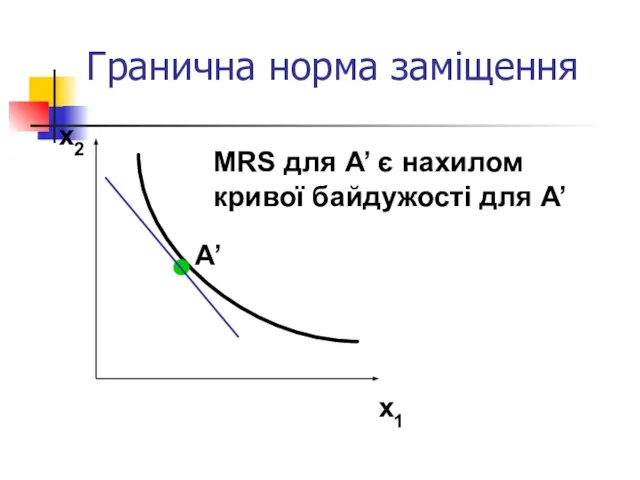
- 38. Гранична норма заміщення x2 x1 А’ MRS для А’ є нахилом кривої байдужості для А’
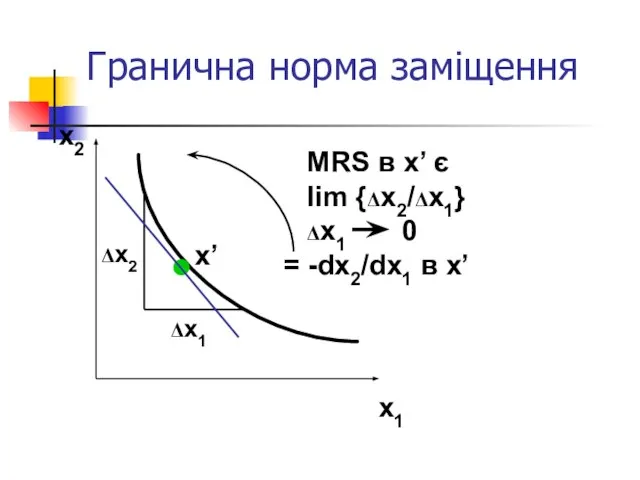
- 39. Гранична норма заміщення x2 x1 MRS в x’ є lim {Δx2/Δx1} Δx1 0 = -dx2/dx1 в
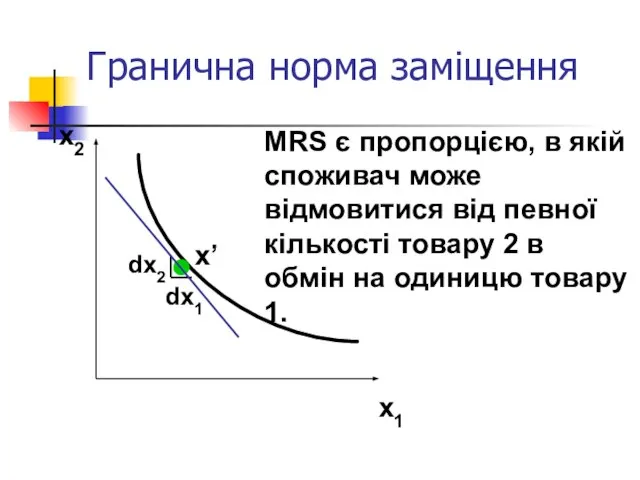
- 40. Гранична норма заміщення x2 x1 dx2 dx1 MRS є пропорцією, в якій споживач може відмовитися від
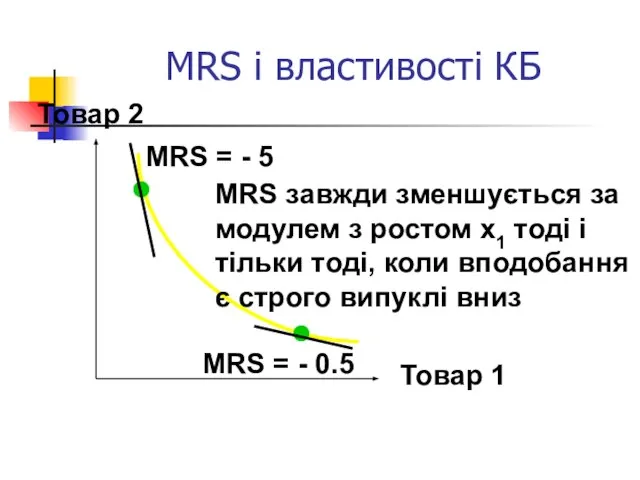
- 41. MRS і властивості КБ Товар 2 Товар 1 MRS = - 5 MRS = - 0.5
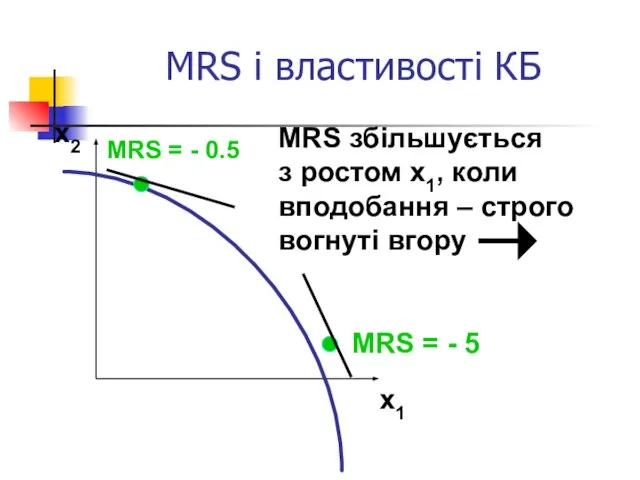
- 42. MRS і властивості КБ x1 x2 MRS = - 0.5 MRS = - 5 MRS збільшується
- 44. Скачать презентацию

















 Основы конституционного строя
Основы конституционного строя Числительные в Английском Языке
Числительные в Английском Языке О генномодифицированных продуктах
О генномодифицированных продуктах  № 1
№ 1 Толковые словари и их создатели
Толковые словари и их создатели Уход за швейной машинкой
Уход за швейной машинкой Развитие профессиональных компетенций маркетологов в вузе
Развитие профессиональных компетенций маркетологов в вузе Доли. Обыкновенные дроби
Доли. Обыкновенные дроби Презентация на тему Луиза Мэй Олкотт "Маленькие женщины"
Презентация на тему Луиза Мэй Олкотт "Маленькие женщины"  Внесение изменений в Федеральный закон О воинской обязанности и военной службе
Внесение изменений в Федеральный закон О воинской обязанности и военной службе Влияние индивидуальных особенностей поведения студентов-спортсменов на психологическое здоровье
Влияние индивидуальных особенностей поведения студентов-спортсменов на психологическое здоровье Логика высказываний Алгоритм построения
Логика высказываний Алгоритм построения Духовная жизнь в 1930-е гг
Духовная жизнь в 1930-е гг ВКР: организация и продвижение музыкального конкурса-фестиваля (заповедник талантов)
ВКР: организация и продвижение музыкального конкурса-фестиваля (заповедник талантов) Лесков «Человек на часах»
Лесков «Человек на часах» О ПРОБЛЕМАХ ИСПОЛЬЗОВАНИЯ НОРМАТИВНЫХ ДОКУМЕНТОВ В РЕМОНТЕ ТУРБОГЕНЕРАТОРОВ Г.В.Ростик - ООО «ЛЭР-ЭЛЕКТРОСЕРВИС» 19-20 октября 2011 г.
О ПРОБЛЕМАХ ИСПОЛЬЗОВАНИЯ НОРМАТИВНЫХ ДОКУМЕНТОВ В РЕМОНТЕ ТУРБОГЕНЕРАТОРОВ Г.В.Ростик - ООО «ЛЭР-ЭЛЕКТРОСЕРВИС» 19-20 октября 2011 г. Исследование алгоритмов поисковых систем, разработка системы прогнозирования позиций сайтов в результатах поисковой выдачи
Исследование алгоритмов поисковых систем, разработка системы прогнозирования позиций сайтов в результатах поисковой выдачи Образование. Процесс образования
Образование. Процесс образования Wie ist das Wetter?
Wie ist das Wetter? Переход к предоставлению услуги «Прием заявлений и организация предоставления гражданам субсидий на оплату жилых помещений и ком
Переход к предоставлению услуги «Прием заявлений и организация предоставления гражданам субсидий на оплату жилых помещений и ком ПРИМЕРНАЯ ПРОГРАММА общеобразовательной дисциплиныИНФОРМАТИКА И ИКТ для НПО и СПО
ПРИМЕРНАЯ ПРОГРАММА общеобразовательной дисциплиныИНФОРМАТИКА И ИКТ для НПО и СПО Презентация на тему Животные Севера
Презентация на тему Животные Севера  Методический семинар Погружение в профессиональное пространство МОУ ДПО «Учебно-методический центр г. Челябинска» Петр
Методический семинар Погружение в профессиональное пространство МОУ ДПО «Учебно-методический центр г. Челябинска» Петр Презентация на тему Государственные таможенные услуги
Презентация на тему Государственные таможенные услуги  Ода методической работе
Ода методической работе Технология личностно-ориентированного обучения
Технология личностно-ориентированного обучения Реклама по антикризисным ценам
Реклама по антикризисным ценам От средневековья к новому времени (7 класс)
От средневековья к новому времени (7 класс)