Минимизация полностью определённых автоматов

Алгоритм минимизации числа внутренних состояний полностью определённого автомата
Находятся последовательные разбиения , ,… множества X до тех пор, пока на каком-то (k+1) шаге не окажется, что это разбиение ничем не отличается от предыдущего. Доказано, что в этом случае ( = ) и есть необходимое нам разбиение, и дальнейшее сокращение числа внутренних состояний автомата невозможно.

Алгоритм минимизации числа внутренних состояний полностью определённого автомата
В каждом классе эквивалентности разбиения выбирается по одному элементу, который образует множество X’.

Алгоритм минимизации числа внутренних состояний полностью определённого автомата
3. Функции переходов и функция выходов для автомата определяются на множестве оставшихся внутренних состояний и множестве входных сигналов. Для этого в таблице переходов вычеркиваются столбцы, соответствующие состояниям, не вошедшим в множество , а в оставшихся столбцах таблицы переходов все состояния заменяются на эквивалентные из множества . В таблице выходов столбцы вычёркиваются.
4. В качестве начального состояния выбирается одно из состояний, эквивалентных X0. На практике лучше взять само X0.

Минимизация автомата Мили
Таблица переходов
Таблица выходов
={X1,X2,X5,X7,X8} B1,
{X3,X4,X6,X9,X10,X11,X12 } B2

Минимизация автомата Мили
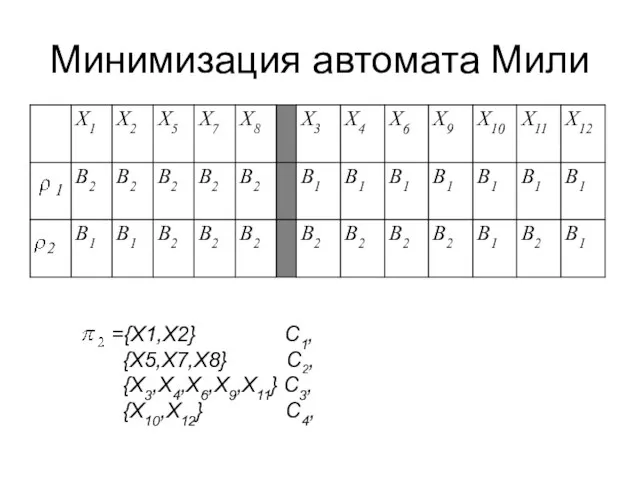
={X1,X2} C1,
{X5,X7,X8} C2,
{X3,X4,X6,X9,X11} C3,
{X10,X12} C4,

Минимизация автомата Мили
= {X1,X2} D1,
{X5,X7} D2
{X8} D3
{X3,X4,X6,X9,X11} D4
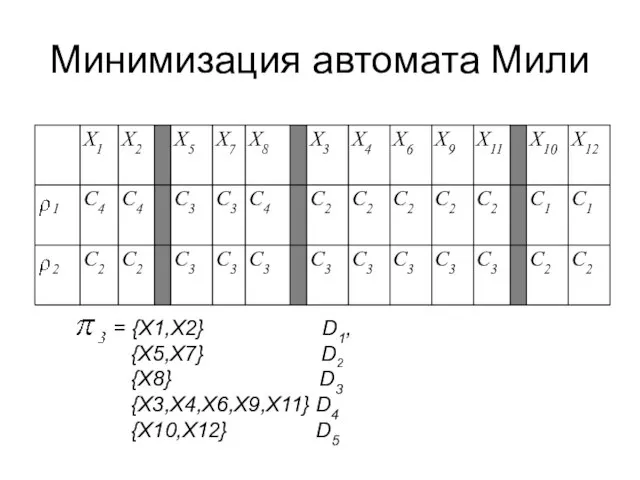
{X10,X12} D5

Минимизация автомата Мили
Таблица переходов
{X1,X2} D1,
{X5,X7} D2
{X8} D3
{X3,X4,X6,X9,X11} D4 {X10,X12} D5

Минимизация автомата Мили
Таблица выходов