Содержание
- 2. Большинство моделей функционирования строятся по математическим схемам. Математические схемы классифицируются в зависимости от типа сигналов и
- 3. F-схема: цифровые двоичные сигналы обрабатываются по детерминированным законам. По F-схеме строятся модели цифровой схемотехники: комбинационных устройств,
- 4. Р-схема: цифровые двоичные сигналы обрабатываются по вероятностным законам. В отличие от F-схемы вместо функций перехода и
- 5. Для математического моделирования сложных информационных систем используется агрегативная схема (А-схема). Математическая модель представляется в виде соединения
- 6. Математическая модель воздействий Вид входных воздействий зависит от используемой математической схемы. Для моделей цифровых автоматов (F-
- 7. Случайные воздействия формируются с использованием генераторов независимых случайных чисел с различными законами распределения, имеющихся практически во
- 8. Метод обратной функции распределения Предположим, что случайная величина X формируется из равномерно распределенной случайной величины U
- 10. Скачать презентацию
Слайд 2Большинство моделей функционирования строятся по математическим схемам. Математические схемы классифицируются в зависимости
Большинство моделей функционирования строятся по математическим схемам. Математические схемы классифицируются в зависимости

Ограничимся двумя типами сигналов: аналоговыми (непрерывными), которые могут принимать любые значения, и цифровыми (бинарными), принимающими два уровня – 0 и 1, и двумя видами обработки: детерминированной и случайной. Четырем возможным сочетаниям соответствуют четыре математических схемы:
• детерминированная обработка аналоговых сигналов – D-схема,
• детерминированная обработка бинарных сигналов – F-схема,
• случайная обработка бинарных сигналов – P-схема,
• случайная обработка аналоговых сигналов – Q-схема.
D-схема: аналоговые сигналы обрабатываются по детерминированным законам. По D-схеме строятся математические модели узлов и устройств аналоговой схемотехники, систем автоматического управления и других систем, которые называют динамическими. От слова dynamic (динамический) и произошло название схемы. Используемый математический аппарат–дифференциальные уравнения. Выходной сигнал однозначно связан с входными сигналами нелинейным дифференциальным уравнением:
Слайд 3F-схема: цифровые двоичные сигналы обрабатываются по детерминированным законам. По F-схеме строятся модели
F-схема: цифровые двоичные сигналы обрабатываются по детерминированным законам. По F-схеме строятся модели
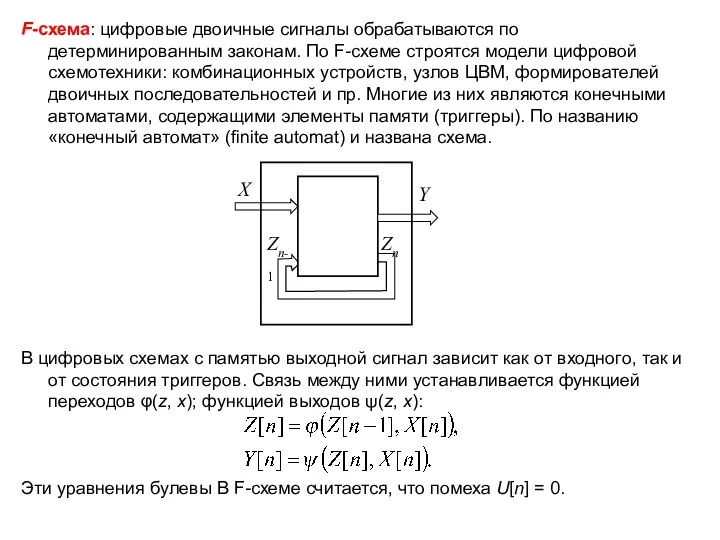
Слайд 4Р-схема: цифровые двоичные сигналы обрабатываются по вероятностным законам. В отличие от F-схемы
Р-схема: цифровые двоичные сигналы обрабатываются по вероятностным законам. В отличие от F-схемы
Вероятностные автоматы могут использоваться как генераторы марковских последовательностей.
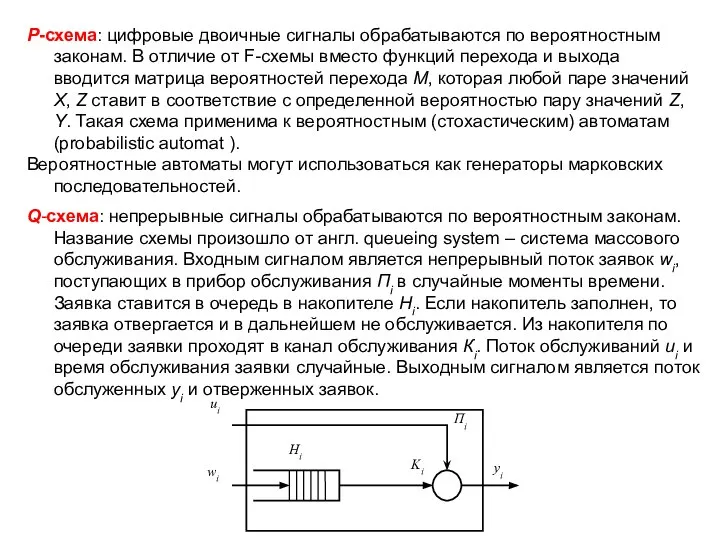
Q-схема: непрерывные сигналы обрабатываются по вероятностным законам. Название схемы произошло от англ. queueing system – система массового обслуживания. Входным сигналом является непрерывный поток заявок wi, поступающих в прибор обслуживания Пi в случайные моменты времени. Заявка ставится в очередь в накопителе Нi. Если накопитель заполнен, то заявка отвергается и в дальнейшем не обслуживается. Из накопителя по очереди заявки проходят в канал обслуживания Кi. Поток обслуживаний ui и время обслуживания заявки случайные. Выходным сигналом является поток обслуженных yi и отверженных заявок.
Слайд 5Для математического моделирования сложных информационных систем используется агрегативная схема (А-схема). Математическая модель
Для математического моделирования сложных информационных систем используется агрегативная схема (А-схема). Математическая модель
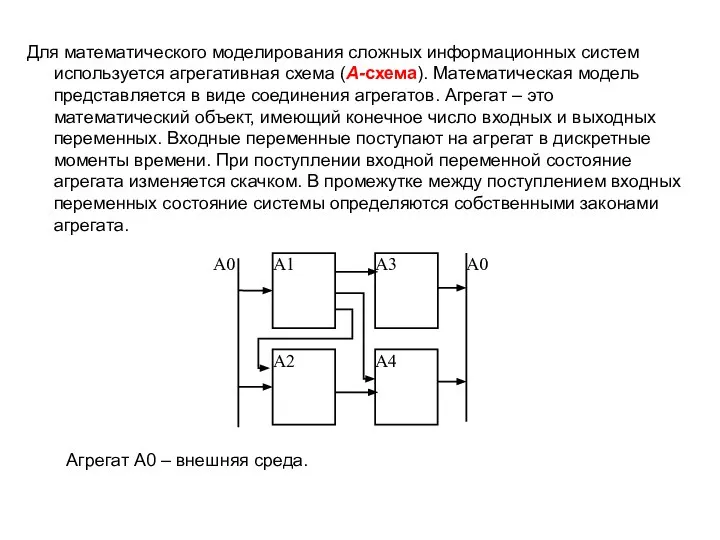
Агрегат А0 – внешняя среда.
Слайд 6Математическая модель воздействий
Вид входных воздействий зависит от используемой математической схемы. Для
Математическая модель воздействий
Вид входных воздействий зависит от используемой математической схемы. Для

Часто использующиеся детерминированные процессы относят к типовым. Например: синусоидальный, треугольный, прямоугольный процессы, скачкообразное, линейное, квадратичное воздействия. Как правило, они уже имеются в используемой программной среде. Если же нужный процесс отсутствует в ППП, то его генерирование производится по формуле, описывающей этот процесс.
При цифровом моделировании любое воздействие представляется в виде последовательности отсчетов, следующих через интервал дискретизации Тд. От выбора интервала дискретизации зависит точность моделирования. В соответствии с теоремой Котельникова-Шеннона непрерывный сигнал с ограниченным спектром восстанавливается без ошибки по его дискретным отсчетам, если Тд ≤ 1/∆fгр, где ∆fгр – граничная частота спектра сигнала.
Слайд 7Случайные воздействия формируются с использованием генераторов независимых случайных чисел с различными законами
Случайные воздействия формируются с использованием генераторов независимых случайных чисел с различными законами

Требование безошибочного моделирования другое! Отсчеты выходного сигнала РЭС через интервал дискретизации Тд в моделируемой непрерывной системе y(t=nTд) и в ее цифровой модели y[nTд] должны быть равными. Требования, при которых эти условия выполняются пока не сформулированы. Но, учитывая, что обработка сигнала в ЦВМ происходит, как правило, при его линейной аппроксимации, следует потребовать, чтобы отличие непрерывного сигнала от его кусочно-линейной аппроксимации было незначительным. Поэтому при моделировании интервал дискретизации берется примерно на порядок меньше, чем по Котельникову.
Наиболее известным методом нелинейного преобразования является метод обратной функции распределения
Слайд 8Метод обратной функции распределения
Предположим, что случайная величина X формируется из равномерно распределенной
Метод обратной функции распределения
Предположим, что случайная величина X формируется из равномерно распределенной
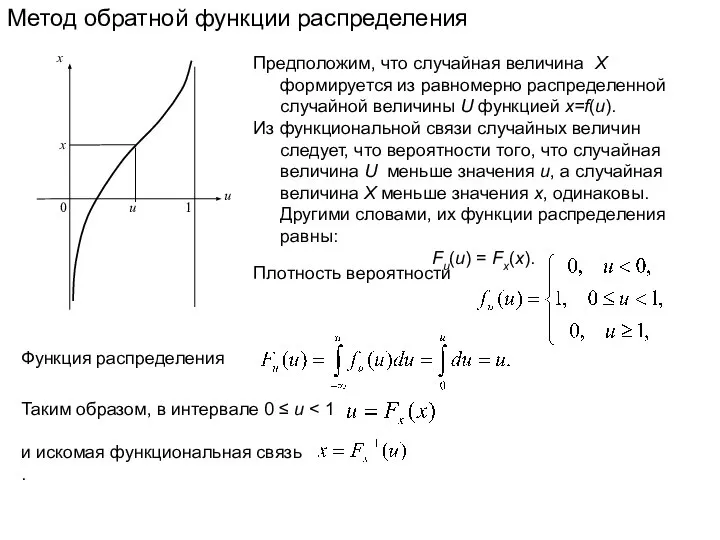
Из функциональной связи случайных величин следует, что вероятности того, что случайная величина U меньше значения u, а случайная величина X меньше значения x, одинаковы. Другими словами, их функции распределения равны:
Fu(u) = Fx(x).
Таким образом, в интервале 0 ≤ u < 1
и искомая функциональная связь
.
 The early middle ages
The early middle ages Римские цифры
Римские цифры Финансовая поддержка Гранта. Правительство Кировской области с участием министерства финансов Кировской области
Финансовая поддержка Гранта. Правительство Кировской области с участием министерства финансов Кировской области Первые художники Земли
Первые художники Земли МОУ «Староильдеряковская средняя школа» Аксубаевского района, РТ.
МОУ «Староильдеряковская средняя школа» Аксубаевского района, РТ. По следам сайтов.
По следам сайтов. VII Всероссийский конкурс учебно-исследовательских экологических проектов «Человек на Земле»
VII Всероссийский конкурс учебно-исследовательских экологических проектов «Человек на Земле» Десятичные дроби. Десятичная запись дробных чисел
Десятичные дроби. Десятичная запись дробных чисел Новые идеи в мире лент
Новые идеи в мире лент Здоровьесберегающая среда: Экологическое пространство Психолого-педагогические факторы: эмоционально-психологический климат в
Здоровьесберегающая среда: Экологическое пространство Психолого-педагогические факторы: эмоционально-психологический климат в  Социальная структура России начала XX века
Социальная структура России начала XX века Человек труда. Выставка работ победителей районного конкурса детского художественного творчества Чишмы
Человек труда. Выставка работ победителей районного конкурса детского художественного творчества Чишмы Тест на тип темперамента (2)
Тест на тип темперамента (2) Династия педагогов
Династия педагогов Янка Дягилева
Янка Дягилева Гражданско-правовое регулирование денежных расчетов в предпринимательской деятельности по законодательству Российской Федерации
Гражданско-правовое регулирование денежных расчетов в предпринимательской деятельности по законодательству Российской Федерации Публикации международного уровня: практические рекомендации
Публикации международного уровня: практические рекомендации ВОЗМОЖНОСТИ ВЛИЯНИЯ ПОТРЕБИТЕЛЕЙ НА КОНЕЧНЫЙ ТАРИФ
ВОЗМОЖНОСТИ ВЛИЯНИЯ ПОТРЕБИТЕЛЕЙ НА КОНЕЧНЫЙ ТАРИФ Творческие работы учащихся на уроках изобразительного искусства
Творческие работы учащихся на уроках изобразительного искусства Презентация на тему Применение аккумуляторов
Презентация на тему Применение аккумуляторов Translation/Interpretation techniques
Translation/Interpretation techniques  Да приемеш вестта за безплодие
Да приемеш вестта за безплодие Техника метания малого мяча
Техника метания малого мяча РОЛЬ КАРТОГРАФИИ В РАЗВИТИИ ОБЩЕСТВА
РОЛЬ КАРТОГРАФИИ В РАЗВИТИИ ОБЩЕСТВА Казачья хата (2 класс)
Казачья хата (2 класс) М1. Занятие 3 (часть 1)
М1. Занятие 3 (часть 1) Психология и профессиональная этика. Воображение
Психология и профессиональная этика. Воображение Анти террор
Анти террор