Содержание
- 2. Моделирование – это метод познания, состоящий в создании и исследовании моделей. Модель – это некий новый
- 3. Модели – упрощенное подобие реального объекта Информационные модели Натуральные модели Формализация – замена натурального объекта его
- 4. Натуральные или материальные модели
- 5. Информационные модели Табличная информационная модель Иерархическая информационная модель Сетевая информационная модель
- 6. В табличной информационной модели перечень однотипных объектов или свойств размещен в первом столбце (или строке) таблицы,
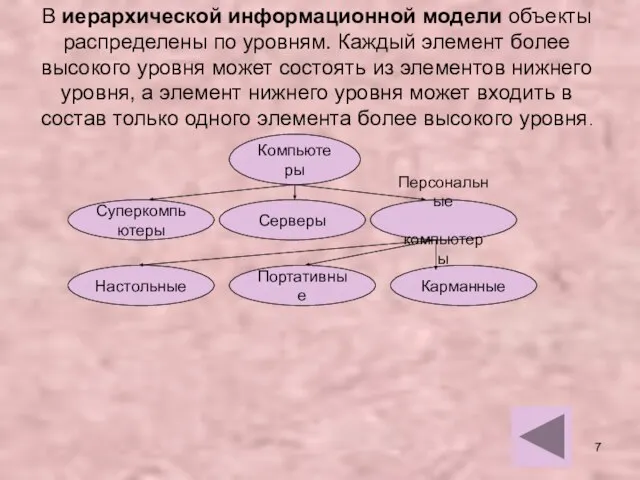
- 7. В иерархической информационной модели объекты распределены по уровням. Каждый элемент более высокого уровня может состоять из
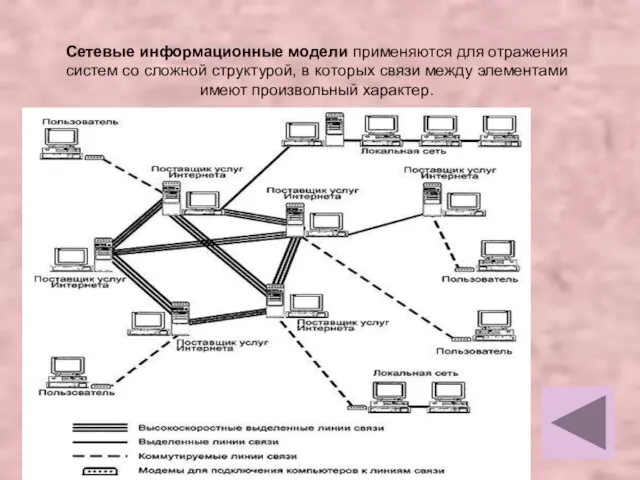
- 8. Сетевые информационные модели применяются для отражения систем со сложной структурой, в которых связи между элементами имеют
- 9. Модели, описывающие состояние системы в определенный момент времени, называются статическими информационными моделями. Модели, описывающие процессы изменения
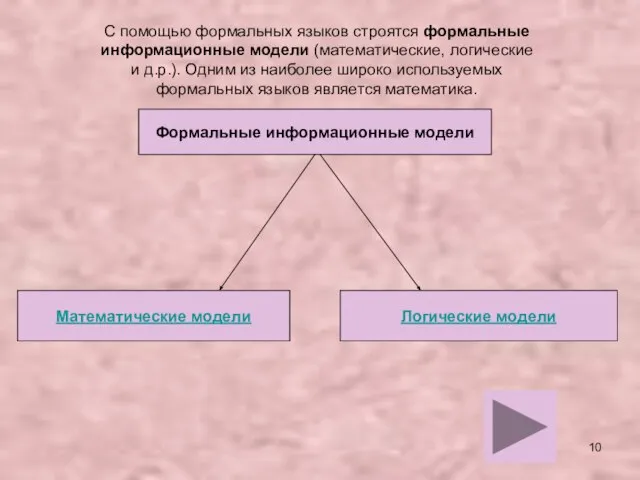
- 10. С помощью формальных языков строятся формальные информационные модели (математические, логические и д.р.). Одним из наиболее широко
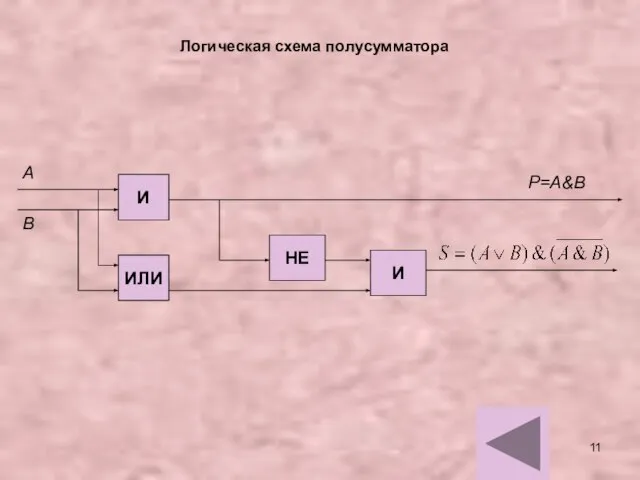
- 11. Логическая схема полусумматора И ИЛИ НЕ И А В Р=А&В
- 12. Математическая модель – это система математических соотношений – формул, уравнений, неравенств и т.д., отражающих существенные свойства
- 13. Основные этапы разработки и исследования моделей на компьютере. Создание описательной информационной модели. Создание формализованной модели. Преобразование
- 14. Математические модели: Приближенное решение уравнений Определение экстремума функции Вычисление площади криволинейной трапеции
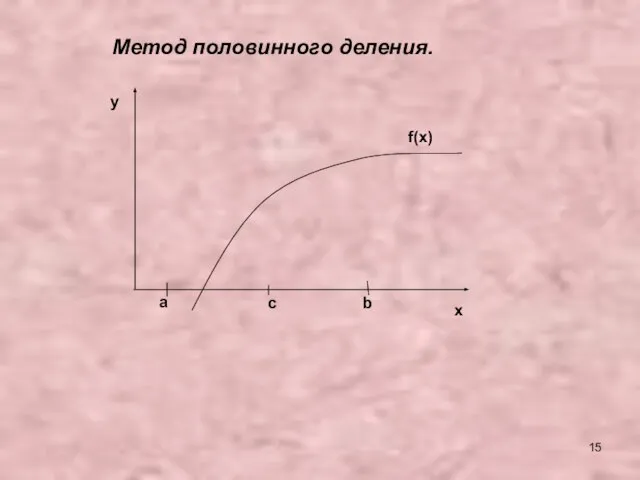
- 15. a b c f(x) y x Метод половинного деления.
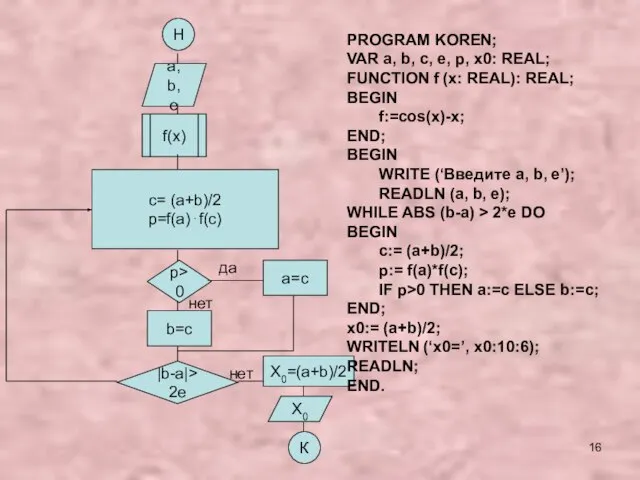
- 16. Н a, b, e f(x) c= (a+b)/2 p=f(a)⋅f(c) p>0 b=c |b-a|>2e X0=(a+b)/2 X0 К a=c да
- 17. Cos(x) – x = 0
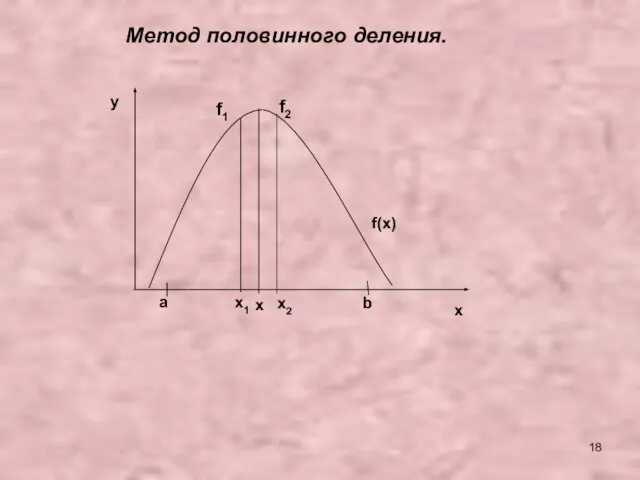
- 18. a b f(x) y x x x2 x1 f1 f2 Метод половинного деления.
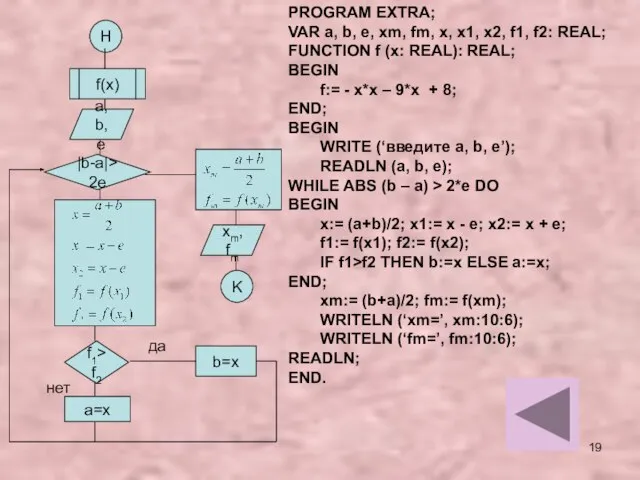
- 19. Н f(x) a, b, e |b-a|>2e f1>f2 a=x xm, fm K b=x PROGRAM EXTRA; VAR a,
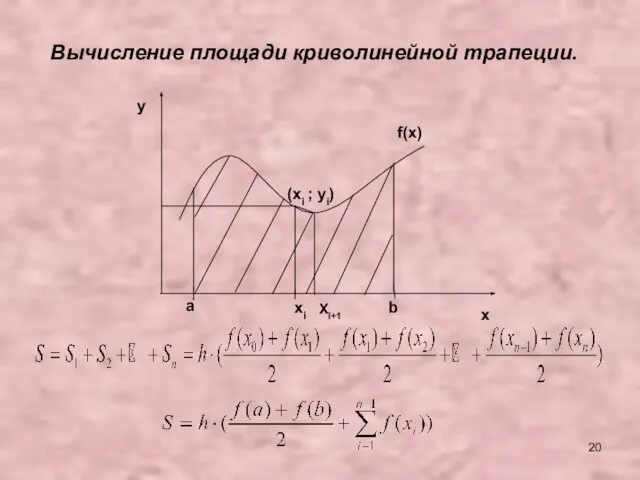
- 20. a b xi f(x) y x (xi ; yi) Вычисление площади криволинейной трапеции. Xi+1
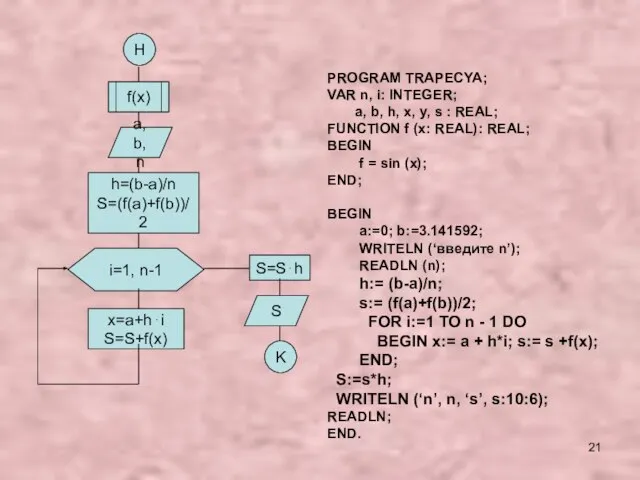
- 21. H f(x) a, b, n h=(b-a)/n S=(f(a)+f(b))/2 i=1, n-1 x=a+h⋅i S=S+f(x) S=S⋅h S K PROGRAM TRAPECYA;
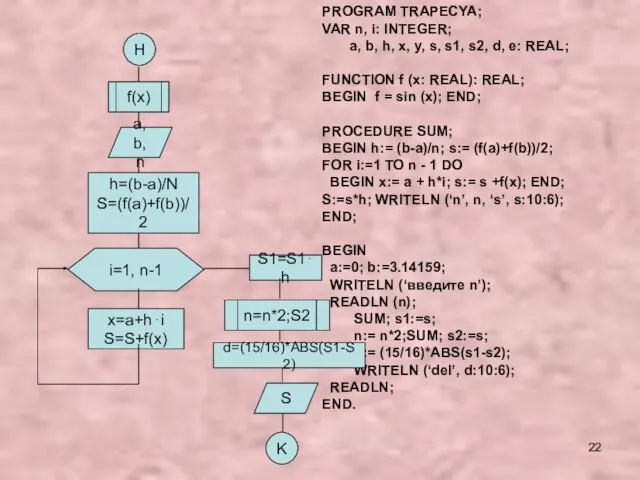
- 22. H f(x) a, b, n h=(b-a)/N S=(f(a)+f(b))/2 i=1, n-1 x=a+h⋅i S=S+f(x) S1=S1⋅h S K PROGRAM TRAPECYA;
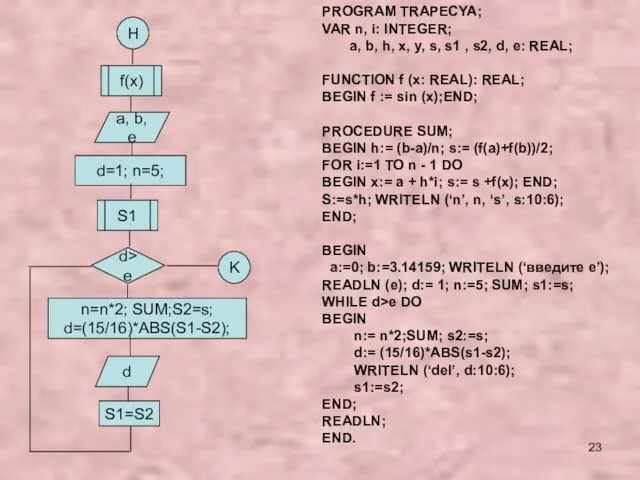
- 23. H f(x) a, b, e d=1; n=5; n=n*2; SUM;S2=s; d=(15/16)*ABS(S1-S2); S1=S2 d K PROGRAM TRAPECYA; VAR
- 24. Вычисление площади криволинейной трапеции с заданной точностью
- 25. Определение погрешности вычисления интеграла
- 27. Скачать презентацию












 Электронный научный журнал Факультета журналистики МГУ им. М.В.Ломоносова «Медиаскоп»
Электронный научный журнал Факультета журналистики МГУ им. М.В.Ломоносова «Медиаскоп» Система работы по формированию портфолио в основной школе
Система работы по формированию портфолио в основной школе Социальная структура: тенденции и противоречия
Социальная структура: тенденции и противоречия Обработка природного материала
Обработка природного материала Жуки
Жуки Web ПорталСлежение за вагонами
Web ПорталСлежение за вагонами Методы выгружения
Методы выгружения Расстановка фигур
Расстановка фигур Организационно-правовые формы предприятий
Организационно-правовые формы предприятий Курсовой проект/разработка урока,основанного на принципах технологий адаптивной школы/
Курсовой проект/разработка урока,основанного на принципах технологий адаптивной школы/ Презентация по профкарьере на тему _Профзаболевания_
Презентация по профкарьере на тему _Профзаболевания_ РЕПУТАЦИЯ И КОРПОРАТИВНЫЙ БРЕНД:
РЕПУТАЦИЯ И КОРПОРАТИВНЫЙ БРЕНД: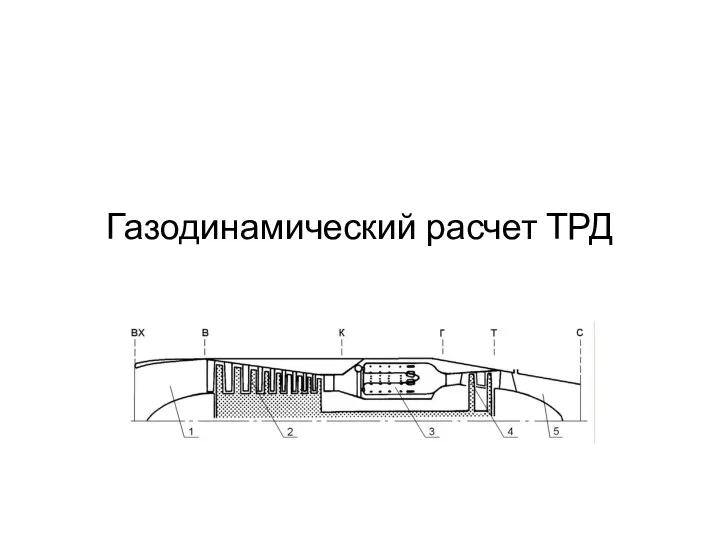 Газодинамический расчет ТРД
Газодинамический расчет ТРД Системно-комплексный контур блоков расчетов бизнесплана
Системно-комплексный контур блоков расчетов бизнесплана Уральский экономический район.
Уральский экономический район. Театральные декорации
Театральные декорации IDE QNX
IDE QNX Декупаж
Декупаж Климат Мордовии Урок географии. 8 класс
Климат Мордовии Урок географии. 8 класс П.А. Столыпину посвящается…
П.А. Столыпину посвящается… Использование в практике преподавания методов диагностического и формирующего оценивания
Использование в практике преподавания методов диагностического и формирующего оценивания Развитие критического мышления
Развитие критического мышления ОРГАНИЗАЦИЯ МОЛОДЕЖНОЙ ПРАКТИКИ Караганда 2011 год
ОРГАНИЗАЦИЯ МОЛОДЕЖНОЙ ПРАКТИКИ Караганда 2011 год Особенность фотосьёмки детей и животных
Особенность фотосьёмки детей и животных Роспись по шелку
Роспись по шелку Многогранники
Многогранники Вредоносные и антивирусные программы. Компьютерные черви и защита от них
Вредоносные и антивирусные программы. Компьютерные черви и защита от них