Многогранники

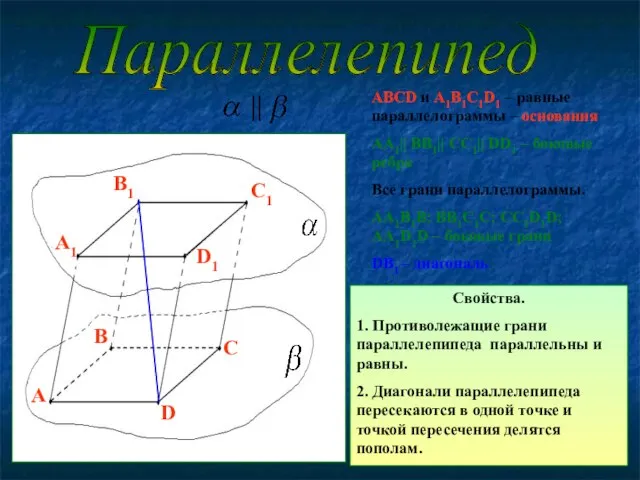
Параллелепипед
АВСD и A1B1C1D1 – равные параллелограммы – основания
АА1|| ВВ1|| СС1|| DD1 – боковые ребра
Все грани параллелограммы.
AA1B1B; BB1C1C; CC1D1D; AA1D1D – боковые грани
DB1 – диагональ
Свойства.
1. Противолежащие грани параллелепипеда параллельны и равны.
2. Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.
А
В
С
D
А1
В1
С1
D1

Прямой параллелепипед
– это параллелепипед, у которого боковые грани являются прямоугольниками.
А
В
С
D
A1
B1
С1
D1
a
b
c

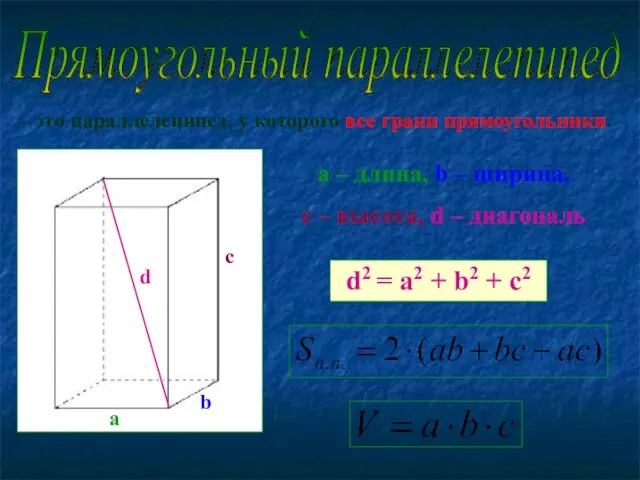
Прямоугольный параллелепипед
– это параллелепипед, у которого все грани прямоугольники.
а
b
c
a – длина, b – ширина,
с – высота, d – диагональ
d
d2 = a2 + b2 + c2

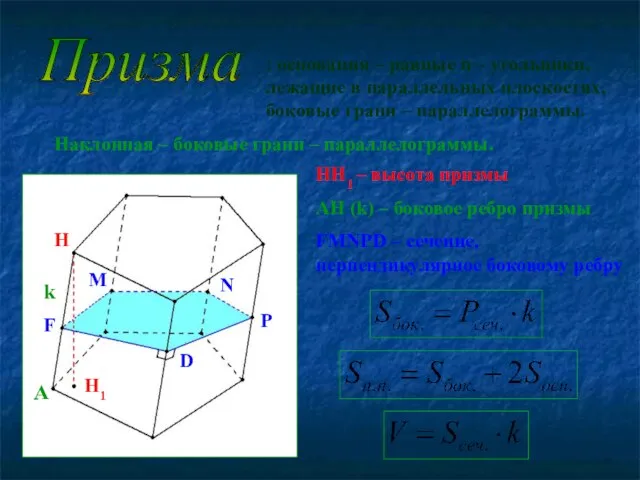
Призма
: основания – равные n – угольники, лежащие в параллельных плоскостях, боковые грани – параллелограммы.
Наклонная – боковые грани – параллелограммы.
H
H1
A
k
F
M
N
P
D
HH1 – высота призмы
AH (k) – боковое ребро призмы
FMNPD – сечение, перпендикулярное боковому ребру

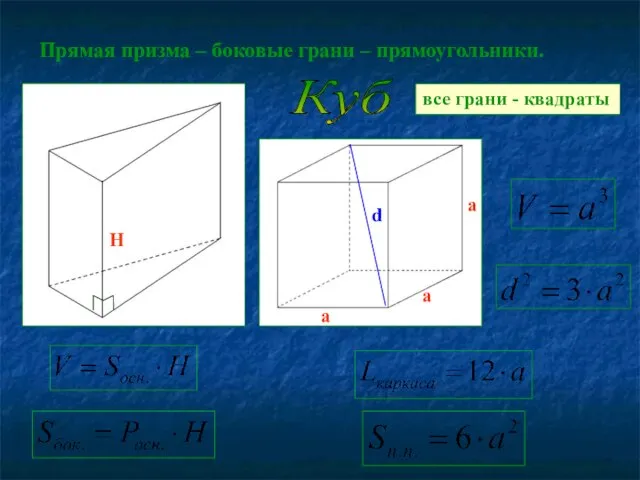
Прямая призма – боковые грани – прямоугольники.
Куб
а
а
а
d
все грани - квадраты
H

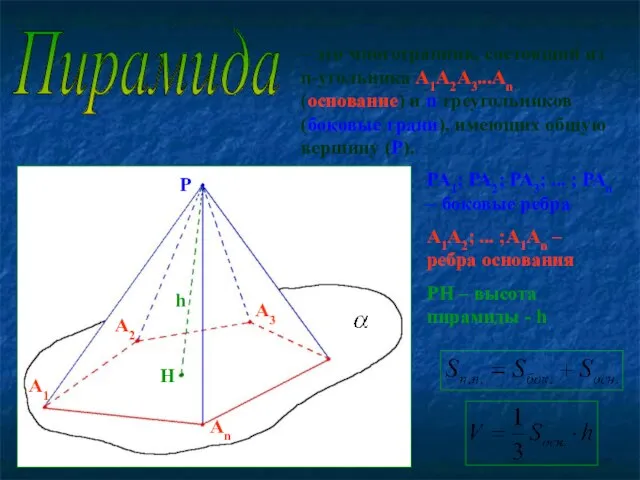
Пирамида
– это многогранник, состоящий из n-угольника А1А2А3...Аn (основание) и n треугольников (боковые грани), имеющих общую вершину (Р).
Р
А1
А2
А3
Аn
H
РА1; РА2; РА3; ... ; РАn – боковые ребра
А1А2; ... ;А1Аn – ребра основания
РH – высота пирамиды - h
h

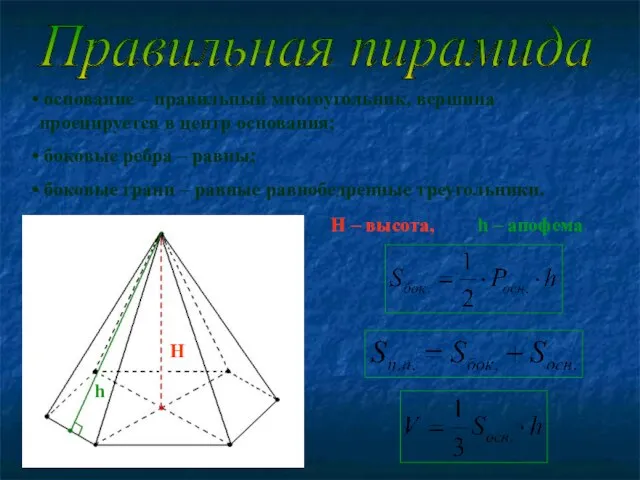
Правильная пирамида
основание – правильный многоугольник, вершина проецируется в центр основания;
боковые ребра – равны;
боковые грани – равные равнобедренные треугольники.
H – высота,
h – апофема
H
h

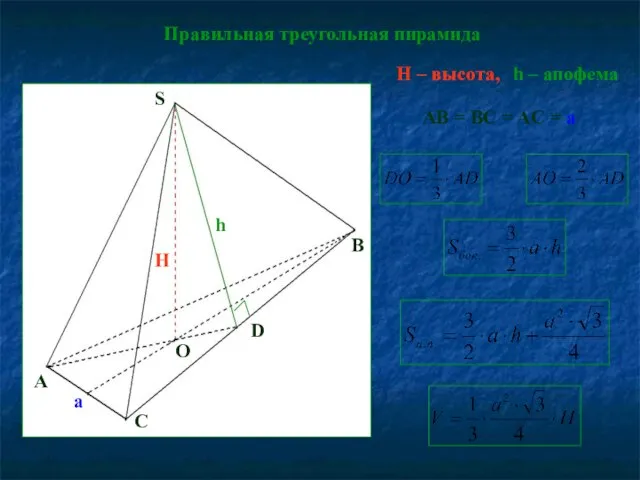
AB = BC = AC = a
Правильная треугольная пирамида
H – высота,
h – апофема
A
O
B
C
h
H
S
D
a

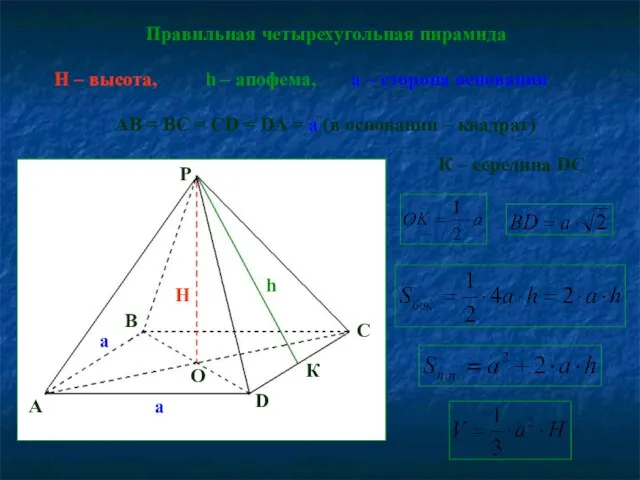
Правильная четырехугольная пирамида
h – апофема,
H – высота,
AB = BC = CD = DA = a (в основании – квадрат)
H
h
a
a
A
B
D
O
P
К
К – середина DC
C
а – сторона основания

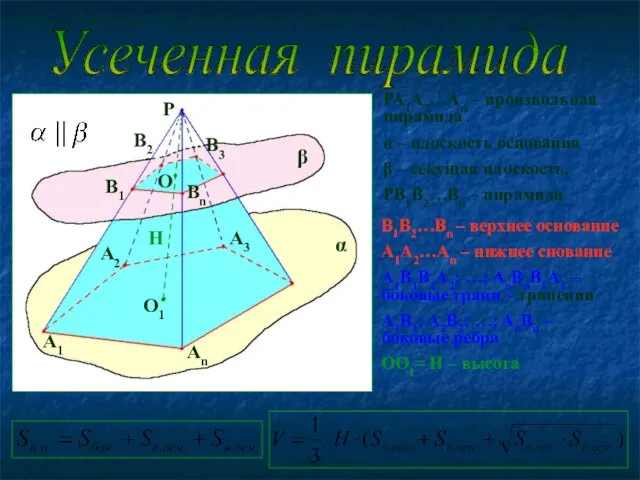
PA1A2…An – произвольная пирамида
α – плоскость основания
β – секущая плоскость,
PB1B2…Bn – пирамида
Усеченная пирамида
β
α
P
A1
A2
A3
An
B1
B3
Bn
B2
O
O1
H
B1B2…Bn – верхнее основание
A1A2…An – нижнее снование
A1B1B2A2; …; AnBnB1A1 – боковые грани – трапеции
A1B1; A2B2; …; AnBn – боковые ребра
OO1= H – высота

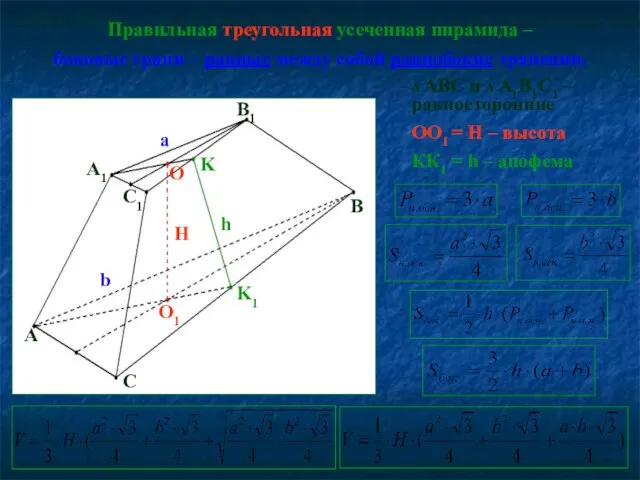
Правильная треугольная усеченная пирамида –
боковые грани – равные между собой равнобокие трапеции.
Δ ABC и Δ A1B1C1 – равносторонние
OO1 = H – высота
КК1 = h – апофема
A
C
A1
B1
C1
O1
O
H
K1
K
h
B
a
b