Молекулярная физика и термодинамика

Она изучает только равновесные
состояния тел,
§§ Введение
02
Термодинамика
или общая теория
теплоты,
изучает общие свойства
макроскопических систем,
отвлекаясь от микроскопического
строения вещества (энергетический
подход).
– равновесные состояния,
непрерывно следующие друг за другом.
а также медленные
процессы

03
Молекулярная физика
изучает строение и свойства вещества,
исходя из атомно-молекулярного
представления
(статистический подход)
и рассматривает
теплоту как беспорядочное движение
атомов и молекул
МФ также называют молекулярно-
кинетической теорией строения
вещества.

При нормальных условиях
1) В 1 см3 воздуха содержится
27 000 000 000 000 000 000 = 2,7∙1019
молекул
2) средняя скорость движения молекул
≈ 500 м/с и она растет с увеличением
температуры
3) средняя длина свободного пробега
молекул ≈ 10–7 м
04
4) за 1 с молекула испытывает около
5 млрд. столкновений

§§ Термодинамическая система
это совокупность макроскопических тел,
обменивающихся энергией между собой
и с другими телами
Физические величины, характеризующие
состояние термодин. системы называются
термодинамическими параметрами
05
Любое изменение в системе, связанное
с изменением хотя бы одного параметра,
называется термодинамическим
процессом

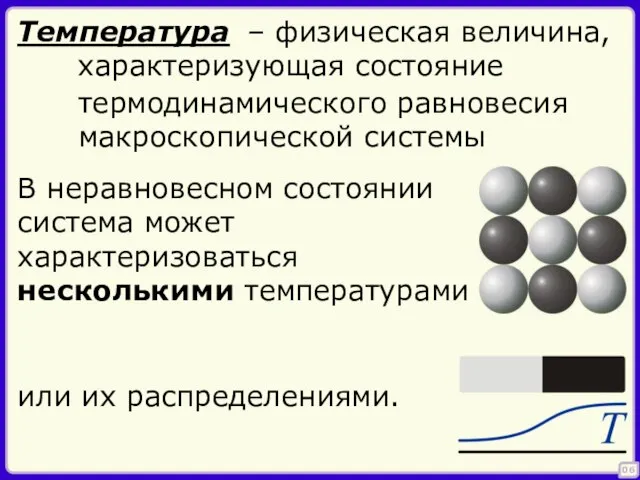
– физическая величина,
характеризующая состояние
06
Температура
термодинамического равновесия
макроскопической системы
В неравновесном состоянии
система может
характеризоваться
несколькими температурами
или их распределениями.

07
Давление
равная отношению силы, действующей
по нормали на некоторую площадку
– физическая величина,
к величине этой площадки
Удельный объем
– величина, обратная
к плотности
если ρ = const, то систему характеризуют
общим объемом V

§§ Уравнение состояния
08
Состояние некоторой массы газа
определяется тремя ТД параметрами:
p – давление, V – объем, T – температура
Уравнение состояния устанавливает
связь между ними:
или
В настоящее время предложено много
(более 100) уравнений состояния,
различающихся точностью и сложностью

§§ Идеальный газ
09
это модель среды (как с.м.т. или а.т.т.),
определяемая положениями:
1) суммарный объем молекул газа
пренебрежимо мал
(по сравнению с объемом сосуда)
2) между молекулами отсутствуют
силы взаимодействия
3) столкновения между молекулами
и стенкой – абсолютно упругие

а также при низком
давлении и при высокой температуре,
10
Нормальные условия
P = 1 атм = 760 мм Hg
≈ 105 Па
1,013250·105 Па
Техническая атмосфера:
0,980665·105 Па
Физическая атмосфера:
Температура: T = 273,15 К (0 °С)
Стандартные условия (химия) :
P = 1 атм, T = 298,15 К (25 °С)
Многие газы при НУ,
можно считать идеальными

11
Уравнение Менделеева–Клапейрона
– число молей газа
M – молярная масса газа, кг/моль
m – масса газа, кг
N – число молекул
NA = 6,022·1023 – число Авогадро
R = 8,31 Дж/(моль∙К)

12
– концентрация молекул, м–3
kB = 1,38∙10–23 Дж/К
– постоянная
Больцмана
Замечание
Уравнение Менделеева–Клапейрона
оказывается справедливым только
при малой плотности реального газа

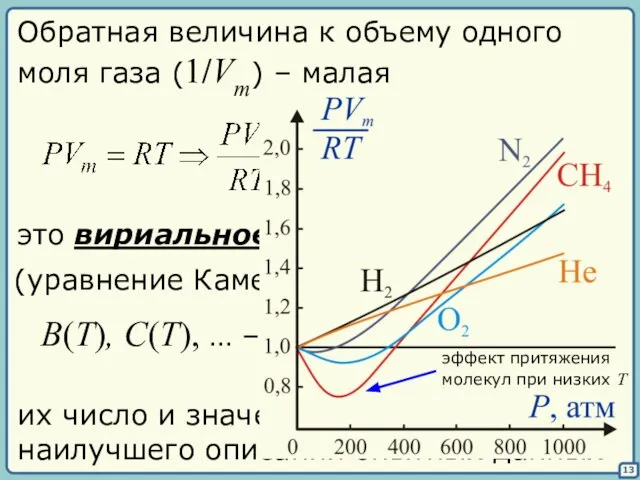
13
Обратная величина к объему одного
моля газа (1/Vm) – малая
это вириальное уравнение состояния
(уравнение Камерлинг-Оннеса, 1901)
B(T), C(T), … – вириальные
коэффициенты
их число и значения выбирают для
наилучшего описания опытных данных

§§ Барометрическая формула
14
Если на газ в сосуде действует сила,
то концентрация молекул установится в
результате действия «противоположных»
факторов:
1) внешнее воздействие
2) хаотическое движение молекул
Пусть на газ действует сила тяжести,
которая не меняется с высотой.
Пусть температура газа постоянна.

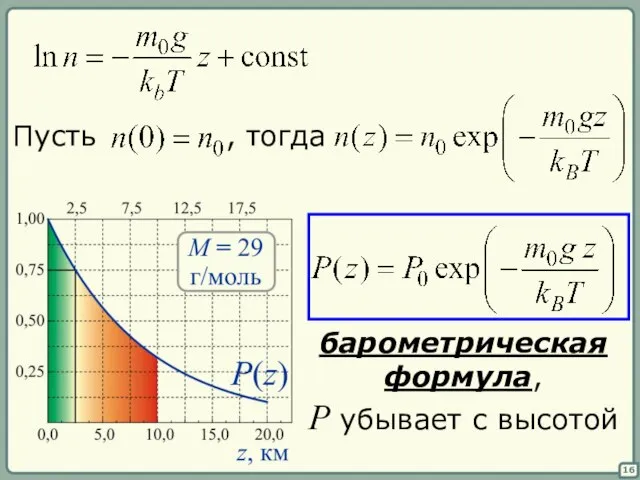
15
Пусть
вычислим интеграл от обеих частей

16
барометрическая
формула,
P убывает с высотой

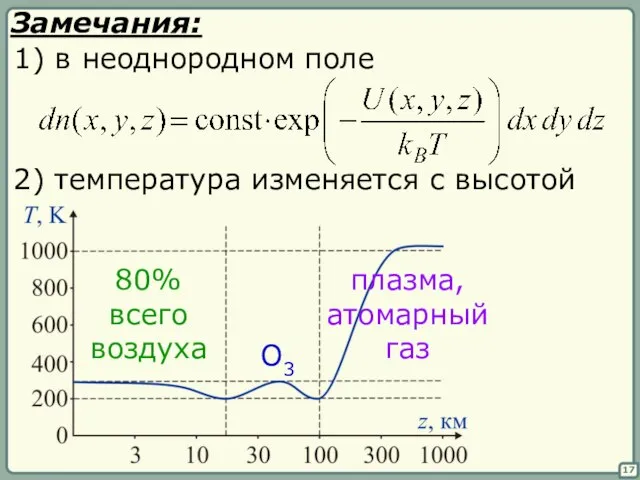
17
Замечания:
1) в неоднородном поле
2) температура изменяется с высотой
80%
всего
воздуха
плазма,
атомарный
газ
O3

§§ Учет объема молекул
18
На очень малых расстояниях между
молекулами действуют силы
отталкивания
N – число молекул
V – объем сосуда
Vmin – объем всех
молекул
(эффективный)
V–Vmin – объем, доступный для
движения молекул

19
Основное уравнение МКТ:
или
Пусть b – минимальный объем 1 моля
(объемная поправка)
тогда
– уравнение Дюпре

20
Величина b обычно принимает
значения 15–60 см3/моль
При увеличении температуры
b уменьшается вместе с
радиусом зоны ограждения.
Например, в 1 м3 воздуха
при н.у. содержится ≈ 40 моль
газа
и собственный объем
молекул ≈ 1,4 литра (0,14 %)
d ≈ 10–9–10–10 м

§§ Внутреннее давление
21
На больших расстояниях между
молекулами действуют силы притяжения
В центре – практически
уравновешены.
Вблизи стенки – сила
направлена к центру.
Следовательно, давление реального газа
выше давления идеального газа,
но на стенку такой газ оказывает
меньшее давление.

22
Пусть x – расстояние от стенки сосуда,
U(x) – потенциальная энергия молекулы
согласно распределению Больцмана
Давление газа на стенку (x = 0):

23
Концентрация молекул возле стенки
V – объем сосуда
Тогда
Сила, действующая на пристеночную
молекулу пропорциональна числу
молекул газа N
, и, следовательно,
U0 – тоже

24
a – константа для данного газа
– уравнение Дитеричи
≈

25
– уравнение Ван-дер-Ваальса

26
P – давление газа на стенку сосуда
– внутреннее давление
– давление газа при
исчезновении сил притяжения
между молекулами.
При пренебрежении внутренним
давлением и объемной поправкой
оно переходит в уравнение

§§ Изобары реального газа
27
Каждый реальный газ представляет
собой ненасыщенный (перегретый) пар,
т.е. при соответствующем понижении
температуры он конденсируется,
превращаясь в жидкость или кристалл
Рассмотрим воду, налитую в
сосуд, закрытый подвижным
поршнем (P = const)
Будем подводить теплоту,
начиная с T = 273 K (0 °С)

28
А: жидкость, T = 273 K
A-B: расширение
жидкости при
нагревании
При дальнейшем подведении тепла вода
начинает испаряться (т.В, T = 373 K)
и объем, занятый водой и паром
начинает быстро расти.
Температура, при этом, остается
постоянной (изотерма = изобаре)

29
C: T = 373 K
В сосуде – жидкость и влажный пар
(содержит капельки жидкости,
увлеченные с поверхности)
D: T = 373 K
Это точка конденсации пара.
В сосуде – сухой насыщенный пар
(капелек не содержит)
E:
При дальнейшем увеличении
температуры пар становится
ненасыщенным (перегретым)

– фазовые
переходы I-го рода, сопровождающиеся
поглощением или выделением теплоты,
30
Кипение и конденсация
изменением состояния и объема.
Теплота, выделяющаяся при ФП I-го
рода (скрытая теплота)
– энергия,
равная отрицательной потенциальной
энергии притяжения молекул
Замечание о критической точке
Чем больше давление, тем больше
расширяется жидкость, прежде чем
закипеть (участок АВ).

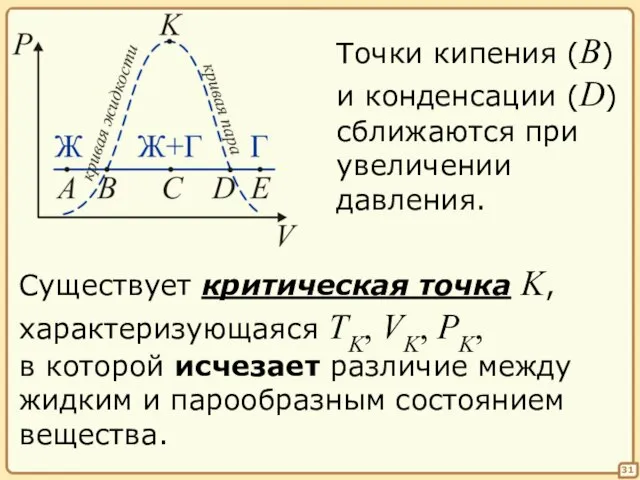
31
Точки кипения (B)
и конденсации (D)
сближаются при
увеличении
давления.
Существует критическая точка K,
характеризующаяся TK, VK, PK,
в которой исчезает различие между
жидким и парообразным состоянием
вещества.

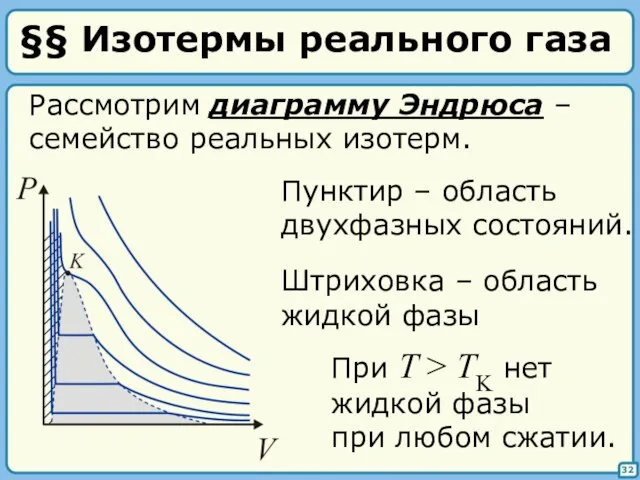
§§ Изотермы реального газа
32
Рассмотрим диаграмму Эндрюса –
семейство реальных изотерм.
Штриховка – область
жидкой фазы
Пунктир – область
двухфазных состояний.
При T > TK нет
жидкой фазы
при любом сжатии.

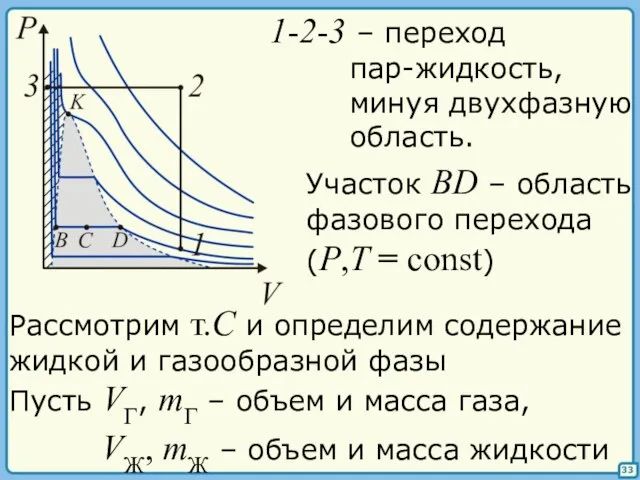
33
1-2-3 – переход
пар-жидкость,
минуя двухфазную
область.
Участок BD – область
фазового перехода
(P,T = const)
Рассмотрим т.C и определим содержание
жидкой и газообразной фазы
Пусть VГ, mГ – объем и масса газа,
VЖ, mЖ – объем и масса жидкости

34
VГ
VЖ
Тогда
(т.к. эта функция должна быть линейной
и в крайних точках совпадать с VB и VD)
или
– правило
рычага

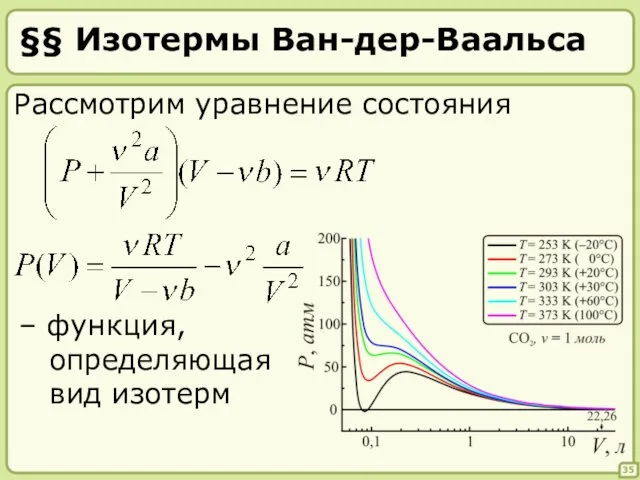
§§ Изотермы Ван-дер-Ваальса
35
Рассмотрим уравнение состояния
– функция,
определяющая
вид изотерм

36
§§ Об уравнениях состояния
Для описания состояния газа в широком
интервале P, V, T необходимо
пользоваться таблично заданным УС.
Для функциональной зависимости
требуется не менее 5 индивидуальных
параметров.
Из рассмотренных уравнений наиболее
точными являются вириальное и
уравнение Дитеричи.

37
Уравнение ВДВ хорошо описывает
состояние газа при низком давлении
и T > TK
Для сжатых газов уравнение оправдано
в немногих случаях (CO2, N2, этилен)
Поведение плотных газов и жидкостей
оно описывает только качественно.
Для описания существенных сторон
физических явлений мы будем
использовать только уравнение
Менделеева–Клапейрона.

§§ Степени свободы молекулы
38
Число независимых координат,
полностью определяющих положение
тела в пространстве,
называется
числом степеней свободы.
Пусть атомы в молекуле
не располагаются на одной
прямой
и связи между
ними не жесткие
Рассмотрим многоатомную молекулу

39
колебательные
степени свободы
Поскольку положения N атомов в
молекуле определяют 3N координат, то
iкол = 3N – (iпост + iвращ)
iпост = 3
iвращ = 3
Энергия молекулы:

40
гипотеза Больцмана (з-н Максвелла)
в т.с., находящейся в состоянии
равновесия,
на каждую поступательную
и вращательную степень свободы
приходится энергия ½kBT
и kBT – на каждую колебательную.
Средняя энергия молекулы:
i = iпост + iвращ + 2iкол

41
Пример: одноатомная молекула
(только поступ. движение)
Пример:
двухатомная молекула
с жесткой связью
– вращением относительно
оси x можно пренебречь

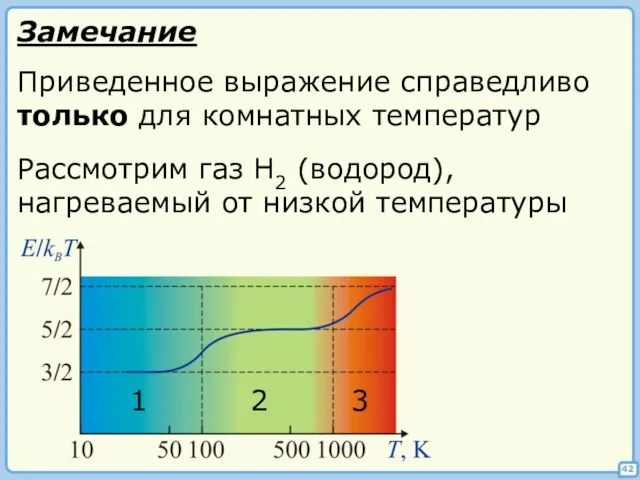
42
Приведенное выражение справедливо
только для комнатных температур
Рассмотрим газ H2 (водород),
нагреваемый от низкой температуры
1
2
3
Замечание

1) Для молекулы, состоящей из любого
числа атомов, i = 3.
Для возбуждения вращательной степени
свободы молекулам необходима
некоторая минимальная энергия
2) В газе есть молекулы с i = 3 и i = 5.
(вращательные уровни «разморожены»)
3) Энергии достаточно для возбуждения
колебательных степеней свободы,
но диссоциация наступает раньше,
чем их полное «размораживание»
43

§§ Средняя скорость молекул
46
Средняя кинетическая энергия молекулы
Средняя квадратичная скорость
Средняя арифметическая скорость

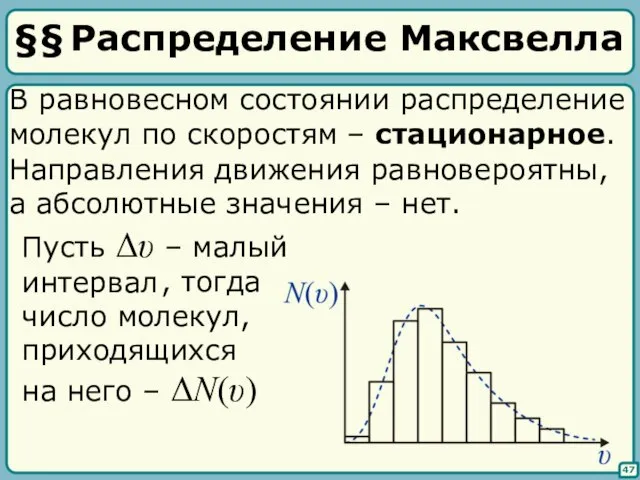
§§ Распределение Максвелла
47
В равновесном состоянии распределение
молекул по скоростям – стационарное.
Направления движения равновероятны,
а абсолютные значения – нет.
Пусть Δυ – малый
интервал
, тогда
число молекул,
приходящихся
на него – ΔN(υ)

48
– функция распределения
молекул по скоростям
– функция распределения Максвелла

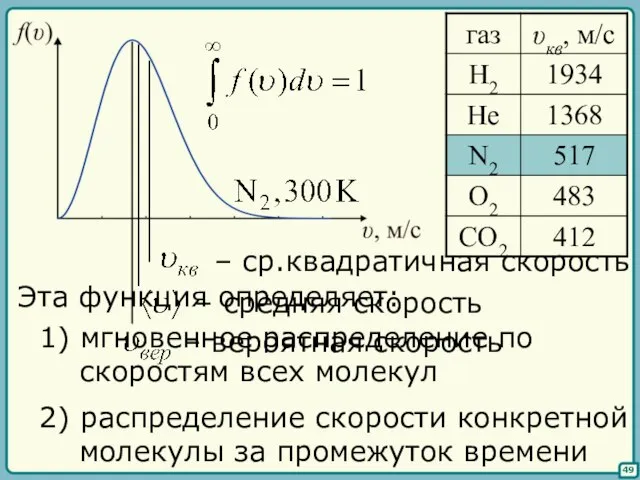
49
Эта функция определяет:
1) мгновенное распределение по
скоростям всех молекул
2) распределение скорости конкретной молекулы за промежуток времени

(плотность
вероятности) иметь молекуле данную
скорость
50
Вычислим наиболее вероятную скорость
Вычислим среднюю скорость.
Учтем, что f(υ) – вероятность

51
Тогда

52
вероятная скорость:
средняя скорость:
ср. квадратичная:
Замечание
Если в сосуде несколько сортов
молекул, то в состоянии равновесия
средние энергии у них – одинаковы

§§ Понятие температуры
53
Распределение молекул по скоростям
у разряженного газа, находящегося
при высокой температуре
описывается
законом Максвелла
В области низких температур

54
В этой области часть реальных газов
имеет распределение Ферми
(кин. энергия у молекул остается и при
T = 0 K)
или распределение Бозе
(движение замирает раньше, чем T = 0 K)
При повышении
температуры
они стремятся
к распределению
Максвелла
область вырождения

55
Понятие температуры сейчас не имеет
наглядного молекулярно-кинетического
представления.
До создания квантовой теории, понятие
температуры было одним из самых
простых, а сейчас – одно из наиболее
сложных.
Под температурой следует понимать
величину, которая устанавливается
независимо от представлений об
идеальном газе.

§§ Длина свободного пробега
, n – концентрация
44
Пусть z – число соударений
за время Δt,
тогда все эти
молекулы находились в
объеме ломанного цилиндра
Пусть d – эффективный
диаметр молекулы
(d ~ 2–3 Å)