Содержание
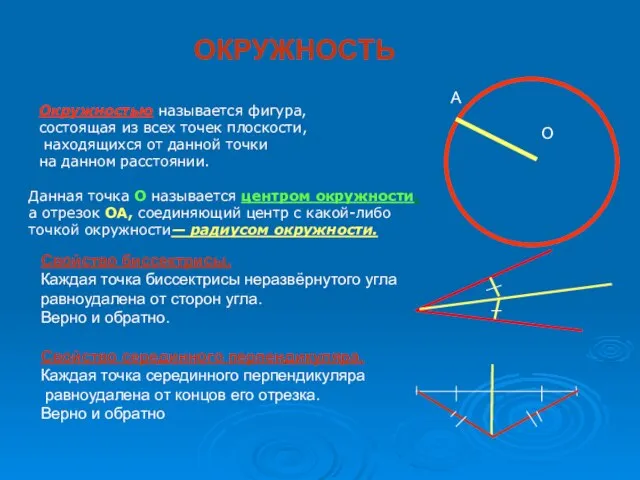
- 2. ОКРУЖНОСТЬ Окружностью называется фигура, состоящая из всех точек плоскости, находящихся от данной точки на данном расстоянии.
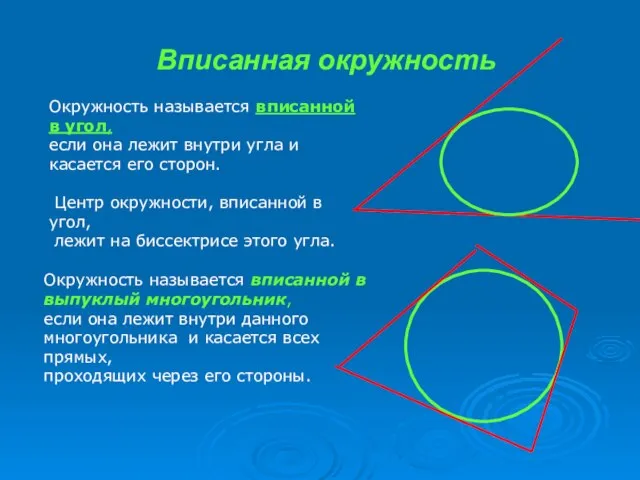
- 3. Вписанная окружность Окружность называется вписанной в угол, если она лежит внутри угла и касается его сторон.
- 4. Если в данный выпуклый многоугольник можно вписать окружность, то биссектрисы всех углов данного многоугольника пересекаются в
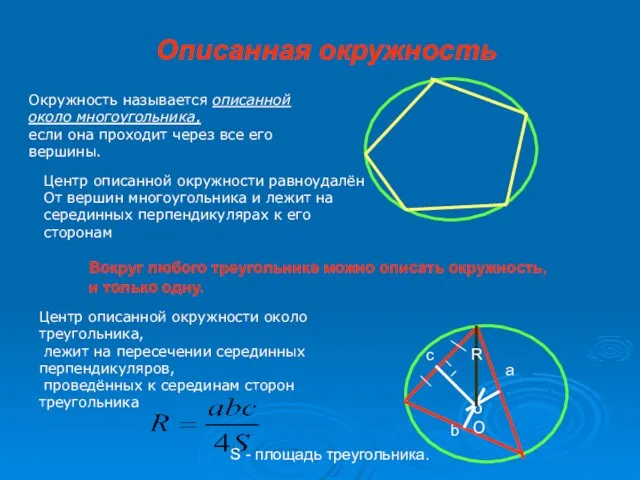
- 5. Описанная окружность Центр описанной окружности равноудалён От вершин многоугольника и лежит на серединных перпендикулярах к его
- 6. Окружность и треугольники Окружность называется вписанной в треугольник, если она касается всех трех его сторон, а
- 7. Окружность и прямоугольный треугольник Радиус вписанной окружности а с b o r a b c R
- 8. Вписанная окружность в четырёхугольник а b c d O r В четырёхугольник можно вписать окружность, если
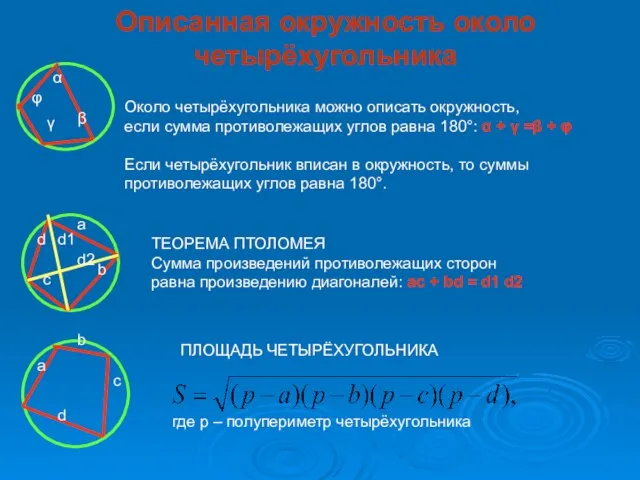
- 9. Описанная окружность около четырёхугольника α β γ φ Около четырёхугольника можно описать окружность, если сумма противолежащих
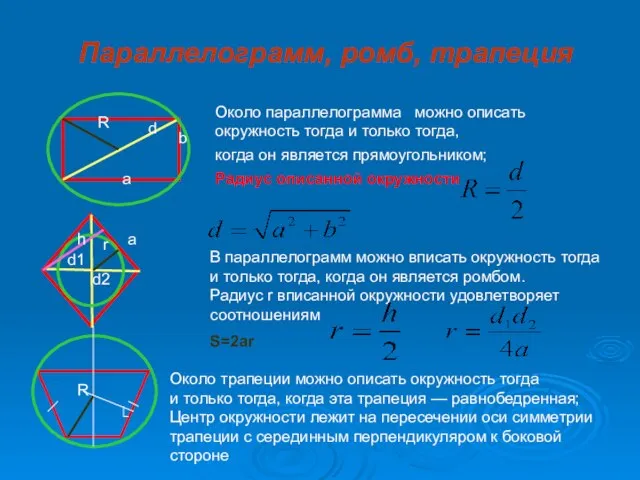
- 10. Параллелограмм, ромб, трапеция Около параллелограмма можно описать окружность тогда и только тогда, когда он является прямоугольником;
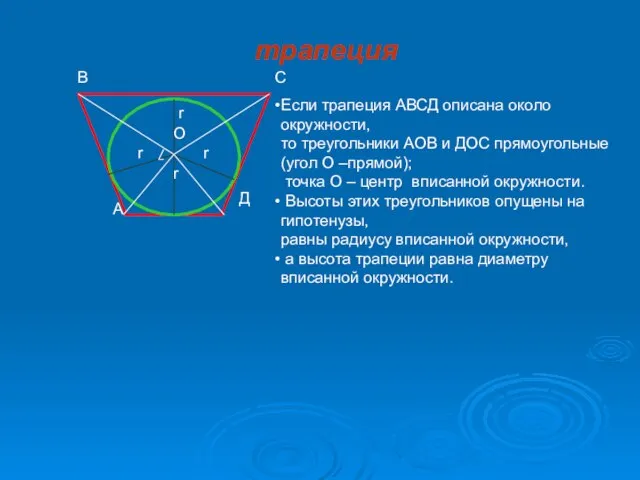
- 11. r r r r А В Д О Если трапеция АВСД описана около окружности, то треугольники
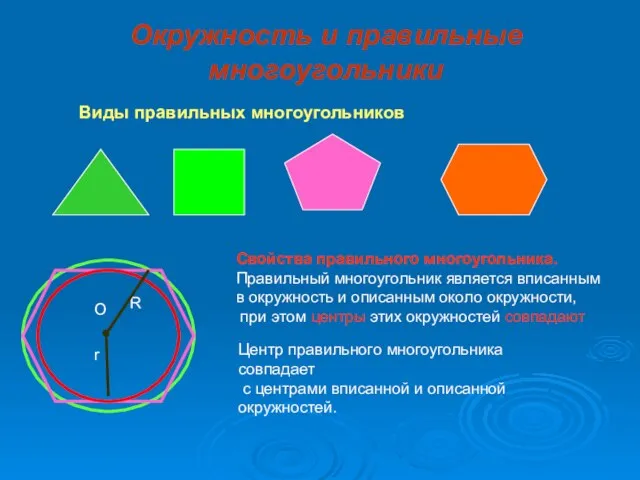
- 12. Окружность и правильные многоугольники Виды правильных многоугольников Свойства правильного многоугольника. Правильный многоугольник является вписанным в окружность
- 13. Основные формулы для правильных многоугольников R r an – сторона многоугольника; R – радиус описанной окружности;
- 14. Список литературы Л. С. Атанасян Учебник геометрии 7-9 класс; Энциклопедия по математике АВАНТА+; Наглядный справочник по
- 16. Скачать презентацию






 Поддержка российских немцев в Западной и Восточной Сибири, на Урале и Дальнем Востоке
Поддержка российских немцев в Западной и Восточной Сибири, на Урале и Дальнем Востоке Кодекс Алиментариус. Международные стандарты пищевых продуктов
Кодекс Алиментариус. Международные стандарты пищевых продуктов Литьё. Что такое литьё?
Литьё. Что такое литьё? Подходы к продаже активов ликвидируемых финансовых организаций:
Подходы к продаже активов ликвидируемых финансовых организаций: poster2021
poster2021 Презентация на тему Трудные дети в школе
Презентация на тему Трудные дети в школе  Формування духовної культури учнів
Формування духовної культури учнів Präsentation der Firma plagon cz, sro
Präsentation der Firma plagon cz, sro Презентация 1
Презентация 1 The composite sentences
The composite sentences  Символы доблести и народной гордости!
Символы доблести и народной гордости! Презентация на тему Генетика и медицина
Презентация на тему Генетика и медицина Планета толерантность
Планета толерантность Презентация на тему Начните работу с нажатия кнопки Пуск
Презентация на тему Начните работу с нажатия кнопки Пуск Развлекательная викторина "Звездный час"
Развлекательная викторина "Звездный час" Презентацiя міни
Презентацiя міни Презентация на тему Изготовление жирафа из пластилина
Презентация на тему Изготовление жирафа из пластилина  Семейные праздники (4 класс)
Семейные праздники (4 класс) Презентация на тему ФАШИЗМ В МЕЖВОЕННОЕ ВРЕМЯ
Презентация на тему ФАШИЗМ В МЕЖВОЕННОЕ ВРЕМЯ  Анализ качества молока от разных производителей
Анализ качества молока от разных производителей Презентация на тему Соли угольной кислоты
Презентация на тему Соли угольной кислоты  Презентация на тему Печатная реклама (PRINT ADVERTIZING)
Презентация на тему Печатная реклама (PRINT ADVERTIZING)  «Основные показатели финансирования отрасли: 2010-2011 г.»Семья и дети
«Основные показатели финансирования отрасли: 2010-2011 г.»Семья и дети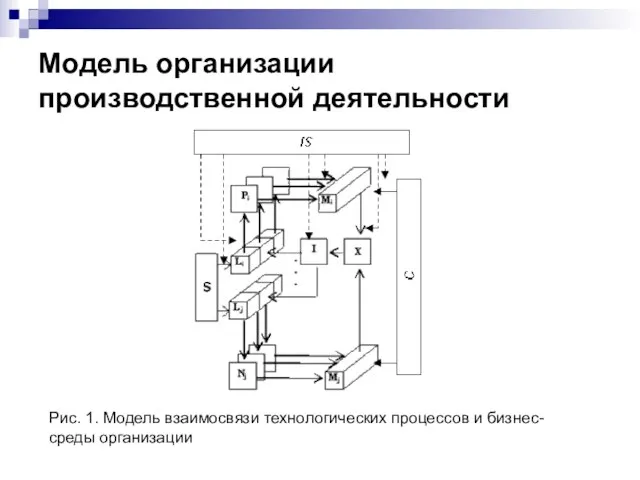 Модель организации производственной деятельности
Модель организации производственной деятельности Единый государственный экзамен (ЕГЭ)
Единый государственный экзамен (ЕГЭ) Презентация на тему Швейцарские банки
Презентация на тему Швейцарские банки  Экопоселения. Шаблон
Экопоселения. Шаблон Отчет. Вопросы бизнесу
Отчет. Вопросы бизнесу