Multilayer model in optics. New analitic results.

Planar multilayer waveguide

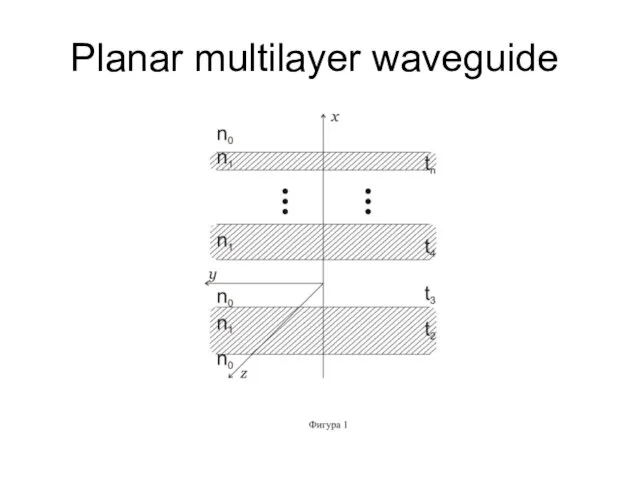
For ТЕ-waves propagating along Oz axis this is a boundary-value problem for the equation

Reduced variables

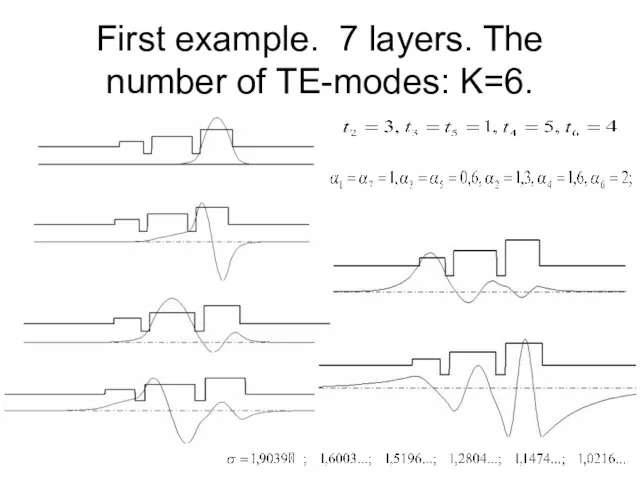
First example. 7 layers. The number of ТЕ-modes: K=6.

Traditional dispersion equations –equations for the eigenvalues of the propagation constant
Type 1 – equation, is obtained by equating to zero of the determinant of homogenius linear system due to boundary conditions.
Type 2 ― equation, obtained by the known method of characteristic matrices
This equations have too many terms if the number of layers is more then 4.
Investigation of waveguides with many layers is now actual.

The properties of the dispersion equations
Th.1. Type 1 equation has roots, coinsiding with the refraction indexes of the inner layers of the waveguide. This roots may not be the eigenvalues of propagation constant.
Th.2. The set of roots of type 2 equation is exactly the set of the eigenvalues of propagation constant.
We propose a new one form of the dispersion equation. This equation in some known cases have no parasitic roots, and moreover it may be treated geometrically.

Multilayer equation

Homogenius variables,vectors

Vectors

Theorem 3. Vectors
rotate counter-clockwise when
is decreasing.
Theorem 4. If
then the directions of this vectors are converging to the direction of Ox axis.

The multilayer equation in vector form

The formulae for the number of TE-modes.

Transform

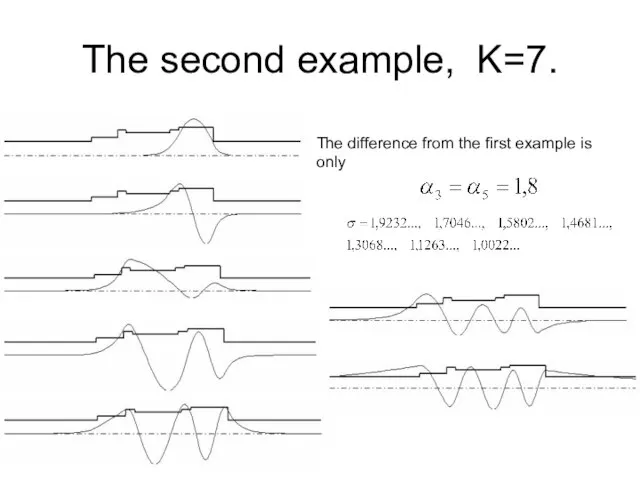
The second example, K=7.
The difference from the first example is only