На рисунке угол DBC равен углу DAC, BO = AO. Докажите, что угол C равен углу D.

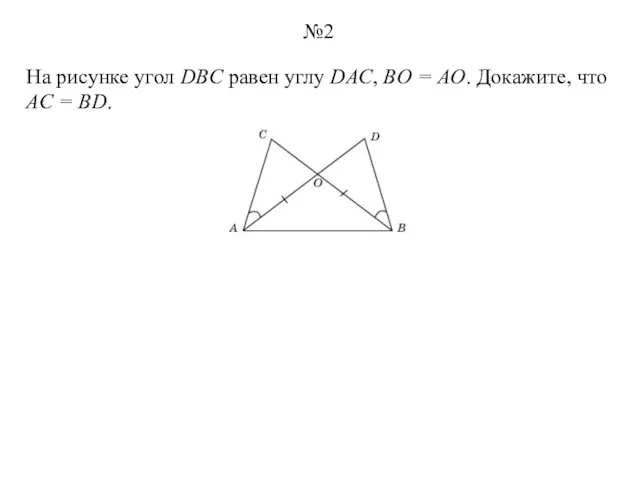
На рисунке угол DBC равен углу DAC, BO = AO. Докажите, что AC = BD.
№2

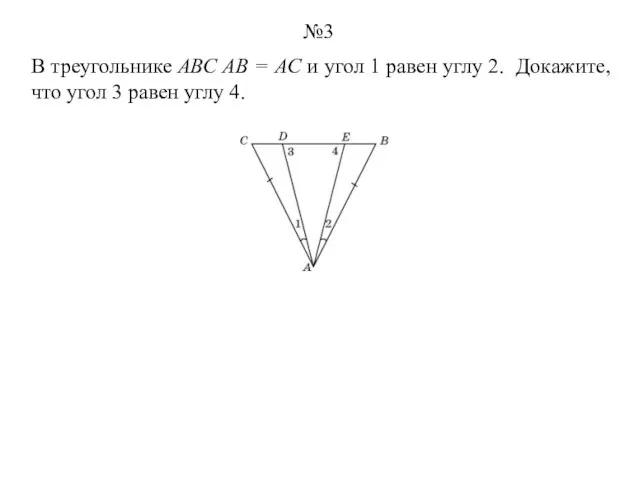
В треугольнике АВС АВ = АС и угол 1 равен углу 2. Докажите, что угол 3 равен углу 4.
№3

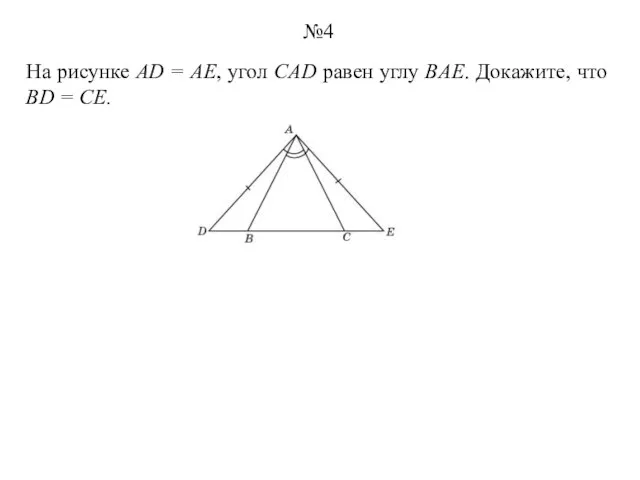
На рисунке AD = AE, угол CAD равен углу BAE. Докажите, что BD = CE.
№4

На рисунке ABC AB = BC. Докажите, что угол 1 равен углу 2.
№5

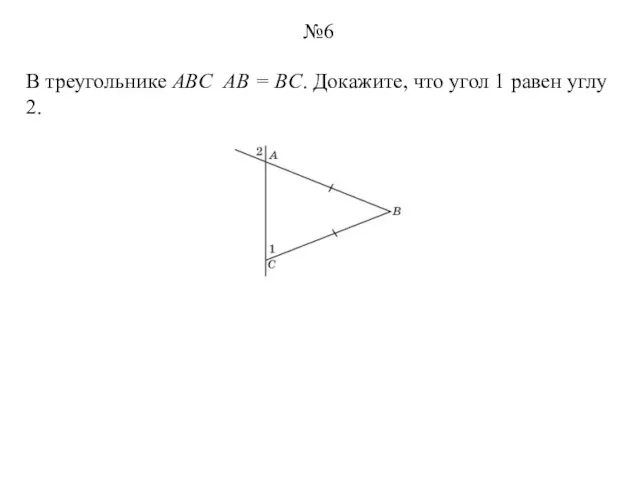
В треугольнике ABC AB = BC. Докажите, что угол 1 равен углу 2.
№6

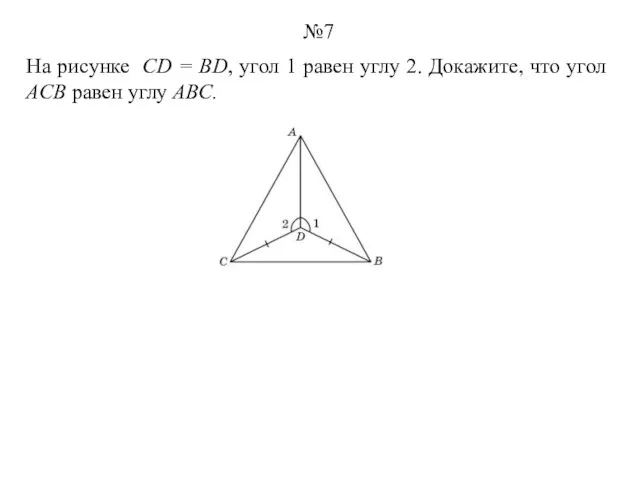
На рисунке CD = BD, угол 1 равен углу 2. Докажите, что угол ACB равен углу ABC.
№7

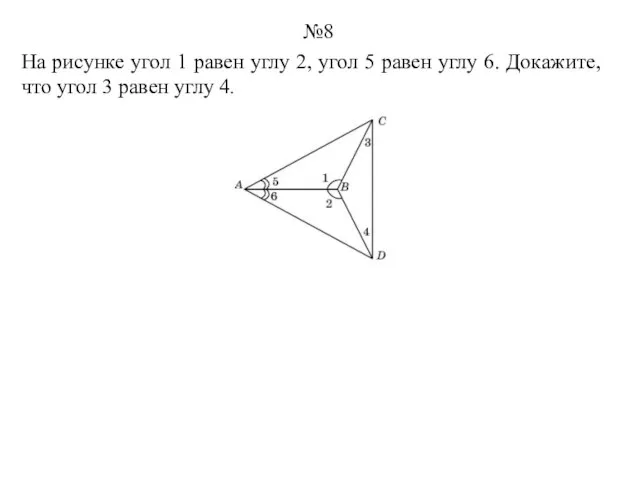
На рисунке угол 1 равен углу 2, угол 5 равен углу 6. Докажите, что угол 3 равен углу 4.
№8

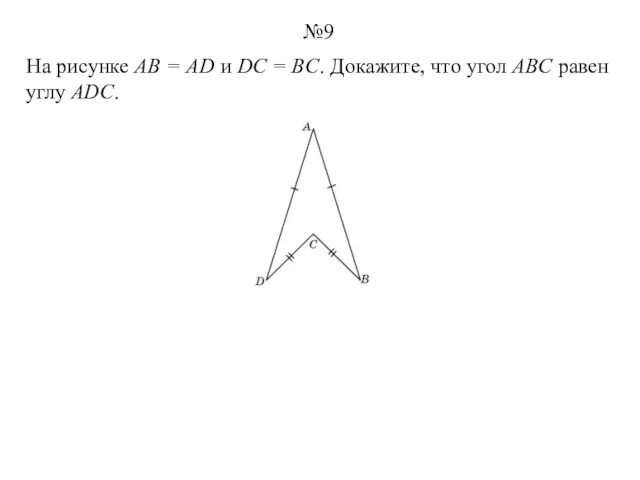
На рисунке АВ = AD и DC = BC. Докажите, что угол ABC равен углу ADC.
№9

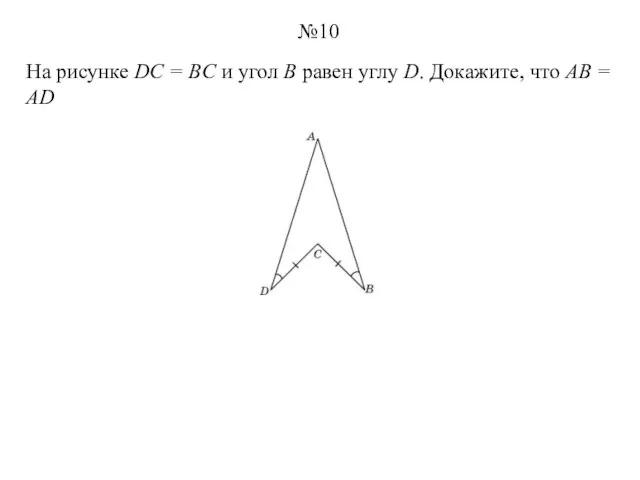
На рисунке DC = BC и угол B равен углу D. Докажите, что АВ = AD
№10

На рисунке AB = BC, CD = DE. Докажите, что угол BAC равен углу CED.
№11

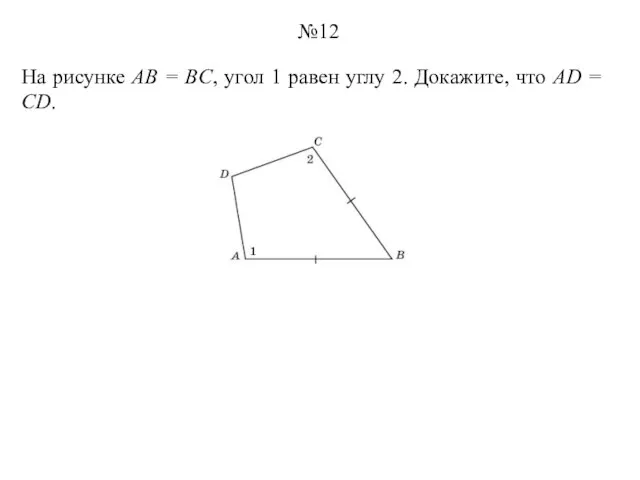
На рисунке AB = BC, угол 1 равен углу 2. Докажите, что AD = CD.
№12

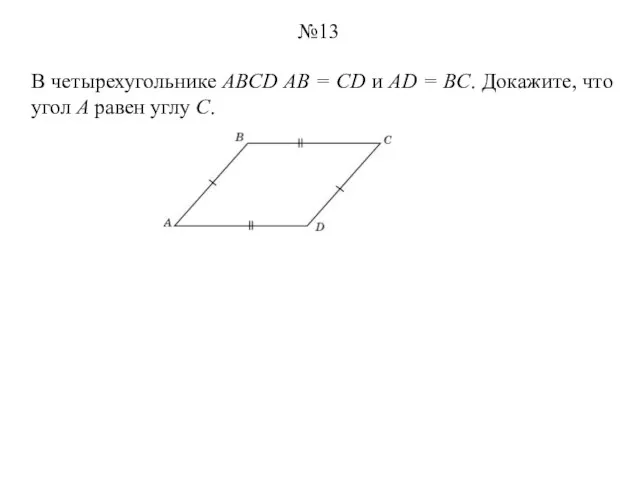
В четырехугольнике ABCD АВ = CD и AD = BC. Докажите, что угол A равен углу C.
№13

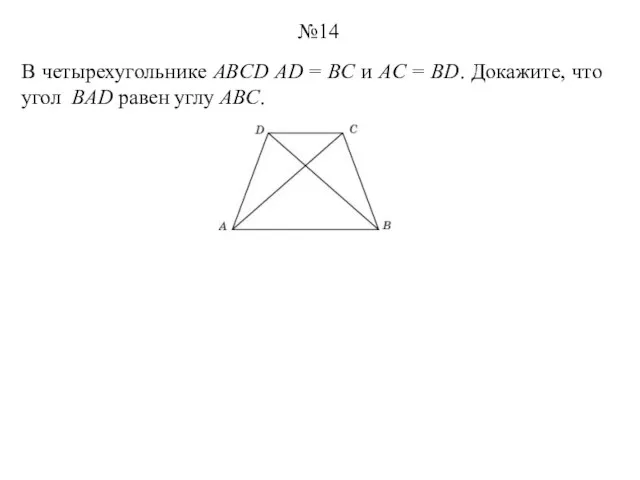
В четырехугольнике ABCD AD = BC и AC = BD. Докажите, что угол BAD равен углу ABC.
№14

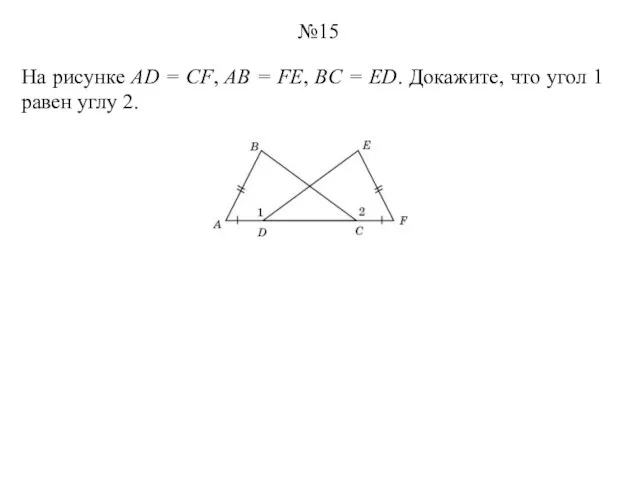
На рисунке AD = CF, AB = FE, BC = ED. Докажите, что угол 1 равен углу 2.
№15

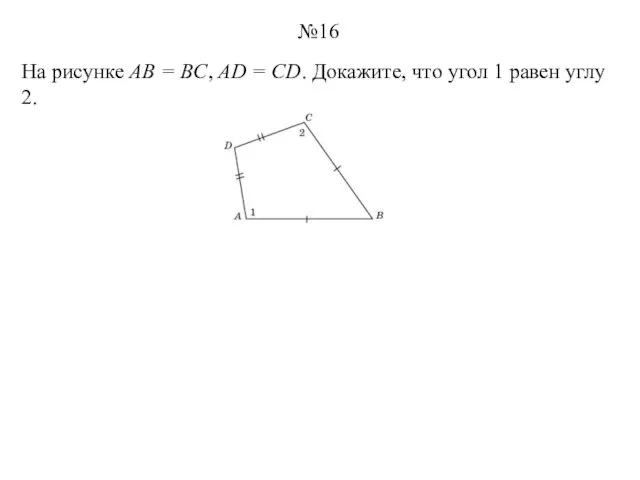
На рисунке AB = BC, AD = CD. Докажите, что угол 1 равен углу 2.
№16

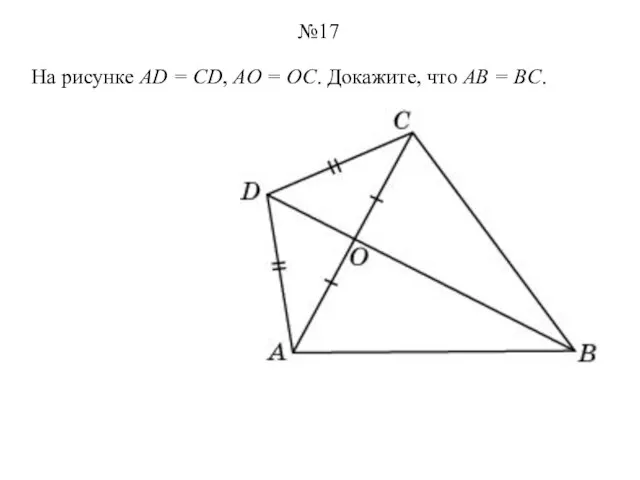
На рисунке AD = CD, AO = OC. Докажите, что AB = BC.
№17

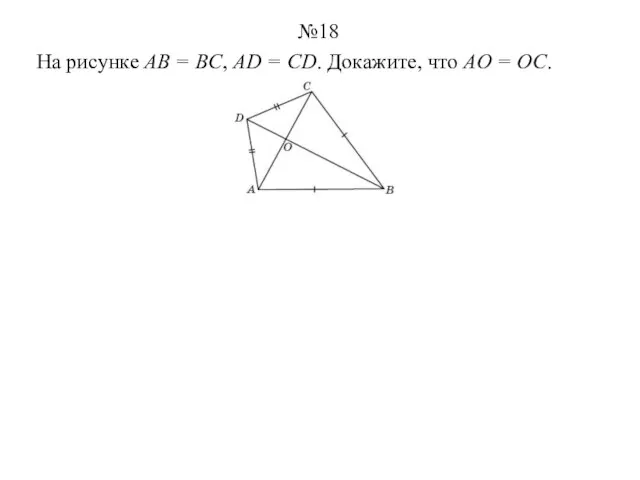
На рисунке AB = BC, AD = CD. Докажите, что AO = OC.
№18

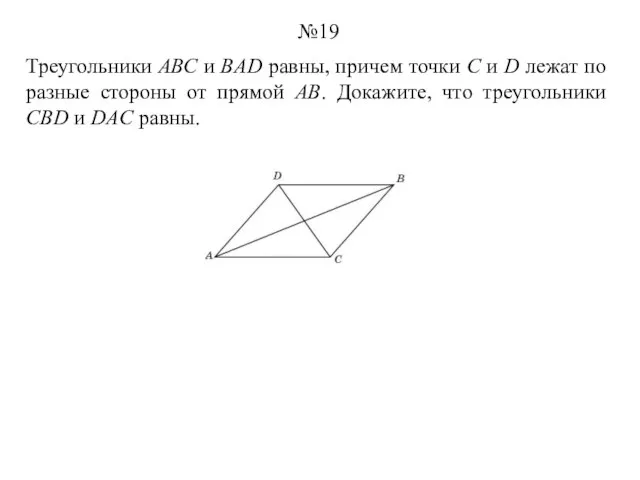
Треугольники АВС и BAD равны, причем точки С и D лежат по разные стороны от прямой АВ. Докажите, что треугольники CBD и DAC равны.
№19

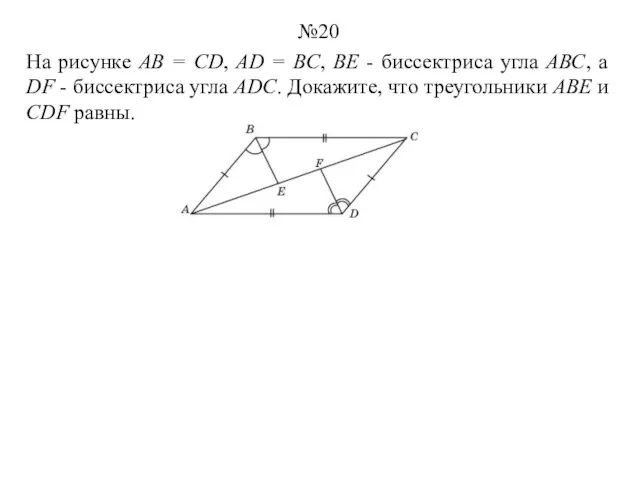
На рисунке АВ = CD, AD = BC, ВЕ - биссектриса угла АВС, а DF - биссектриса угла ADC. Докажите, что треугольники ABE и CDF равны.
№20

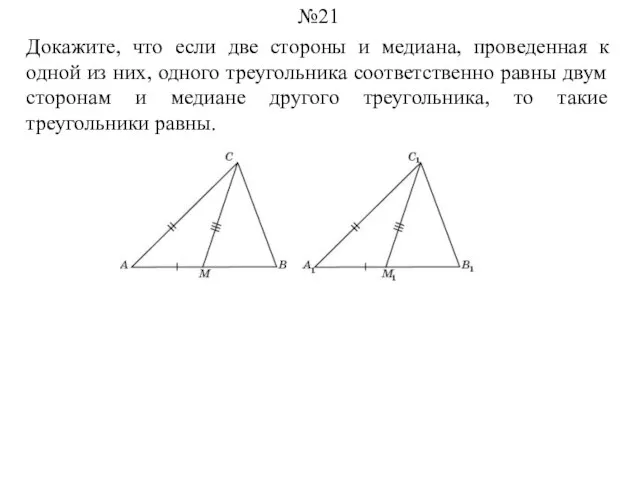
Докажите, что если две стороны и медиана, проведенная к одной из них, одного треугольника соответственно равны двум сторонам и медиане другого треугольника, то такие треугольники равны.
№21

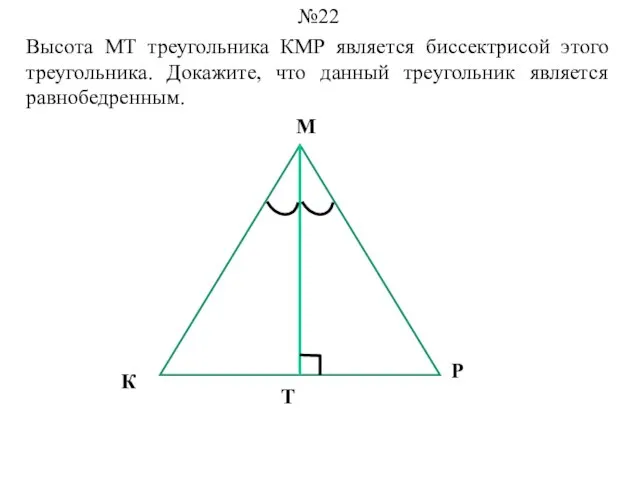
Высота МТ треугольника КМР является биссектрисой этого треугольника. Докажите, что данный треугольник является равнобедренным.
№22
М
К
Р
Т