Содержание
- 2. 1 часть: 8 заданий с кратким ответом базового уровня 2 часть: 4 задания с кратким ответом
- 3. Выполняем внимательно Не пишем в бланке ответов после числа единицы измерений Не пишем карандашом (после сканирования
- 4. Минимум записей, но достаточный для того, чтобы контролировать решение, выполняя обратное действие, найти ошибку. Устный счет
- 5. Знание приемов решения разных задач Знание алгоритмов решения различных уравнений: Линейные уравнения Квадратные уравнения Рациональные уравнения
- 6. О потере корней -деление обеих частей уравнения на одно и то же выражение -сужение ОДЗ в
- 7. Знать формулы
- 8. Задачи-ловушки
- 9. Правило за 100% брать ту величину, с которой мы сравниваем Пример. Шесть одинаковых рубашек дешевле куртки
- 10. Формулы для решения задач на проценты
- 11. Решаем 1 часть максимально быстро. На чем можно сэкономить? При решении задачи на смеси 0,3х+0.6у+5=0,41(х+у+10); 0,3х+0,6у=0,36(х+у+10)
- 12. Задание №13 ОТНОСИТЕЛЬНО НЕТРУДНОЕ УРАВНЕНИЕ Может содержать тригонометрические функции, логарифмы, степени, корни, показательную функцию Как правило,
- 13. Типичные ошибки в задании №13 Использование формулы корней для простейшего тригонометрического уравнения относительно синуса – к
- 14. Типичные ошибки в задании № 13 По-прежнему, как и в прошлых годах, учащиеся теряют баллы в
- 15. Различные способы отбора корней 1. Арифметический способ: а) непосредственная подстановка полученных корней в уравнение и имеющиеся
- 16. Задания №14 и №16 Проверяют умения выполнять действия с геометрическими фигурами В первом пункте – доказать
- 17. Задание №15 Неравенство, содержащее степени, дроби, корни, логарифмы (в том числе, с переменным основанием). Традиционно выполняемые
- 18. Задание №17 Задача с экономическим содержанием Проблемы Неумение работать с процентами Неумение правильно считывать условие Неумение
- 19. Задание №18 Задача с параметром Нужно постараться решить эту задачу или хотя бы продвинуться в ее
- 20. Задание №19 Задание олимпиадного типа Для ее решения не требуется никаких специальных знаний, выходящих за рамки
- 21. ЕГЭ 2017 (досрочный) 19. На доске написано несколько различных чисел, произведение любых двух из которых больше
- 22. О проверке работ и об апелляции Каждая работа проверяется 2 независимыми экспертами При расхождении оценки двух
- 24. Скачать презентацию





















 Функционирование организации коммерческого типа в условиях рынка
Функционирование организации коммерческого типа в условиях рынка Тема: “Школьная перепись” выполнила: ученица 7 класса Савчук Татьяна
Тема: “Школьная перепись” выполнила: ученица 7 класса Савчук Татьяна  Презентация музыкально- педагогической деятельности
Презентация музыкально- педагогической деятельности Система образования во Франции
Система образования во Франции Loch Ness Monster
Loch Ness Monster 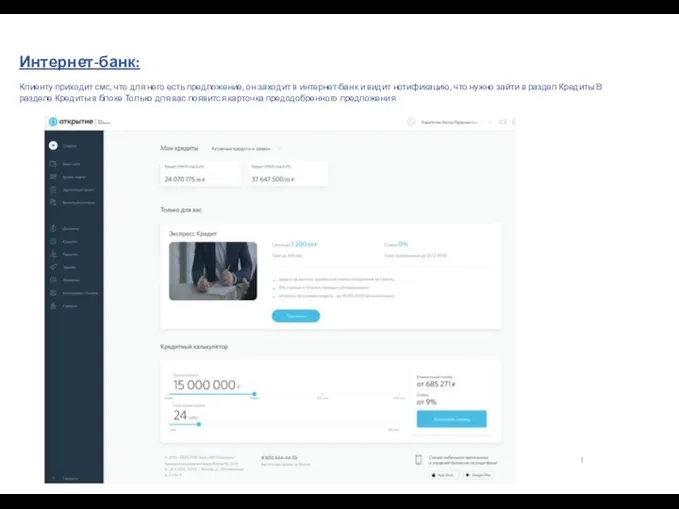 Интернет-банк. Инструкция по оформлению кредитов
Интернет-банк. Инструкция по оформлению кредитов Зона отдыха в школе. Проект
Зона отдыха в школе. Проект самооценка
самооценка Волонтерский сектор РязГМУ
Волонтерский сектор РязГМУ Тема № 7.1
Тема № 7.1 Лидерство
Лидерство Мировая цифровая библиотека
Мировая цифровая библиотека Искуственный интелект
Искуственный интелект Презентация на тему Речь младших школьников и пути её развития
Презентация на тему Речь младших школьников и пути её развития Тема: обобщающий урок по теме глагол. ( 3 класс)
Тема: обобщающий урок по теме глагол. ( 3 класс) КРО: как повысить продажи с сайта, не потратив ни копейки
КРО: как повысить продажи с сайта, не потратив ни копейки Покорители свободных Греков
Покорители свободных Греков Загадки назови профессию
Загадки назови профессию Презентация на тему Сочинение по картине «Друзья»
Презентация на тему Сочинение по картине «Друзья»  Авиационная фанера. Виды и назначение
Авиационная фанера. Виды и назначение Раздел 3 Зрелое Средневековье Готический стиль XIII - XV века
Раздел 3 Зрелое Средневековье Готический стиль XIII - XV века Электронные таблицы. Термины и понятия
Электронные таблицы. Термины и понятия Слуховой, вестибулярный анализаторы
Слуховой, вестибулярный анализаторы Ориентирование
Ориентирование Принятие Христианства на Руси
Принятие Христианства на Руси «Как заработать и при этом ничего не продавать»
«Как заработать и при этом ничего не продавать» Особо охраняемые природные территории Липецкой области
Особо охраняемые природные территории Липецкой области врол
врол