Начало множеств 2021

Множество – это объект, образованный за счет мысленного собирания в единое целое каких-либо предметов, в том числе, возможно, и самих множеств.
Элементы множества обозначают буквами латинского алфавита a, b, c,…, а сами множества – прописными буквами А, В, С,….
Множество задано, если известно, из каких элементов (предметов) оно состоит.

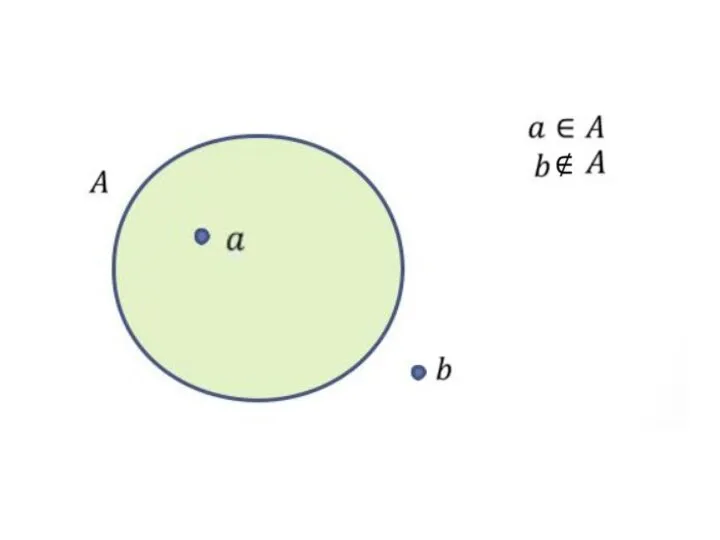
Пустое множество не содержит ни одного элемента и обозначается ø .
Запись означает, что элемент принадлежит множеству .
Множества изображают с помощью диаграмм Эйлера-Венна

Множества бывают конечные и бесконечные.
Примеры:
1) множество жителей г. Москвы конечное;
2) множество натуральных чисел бесконечное.

Задание множеств осуществляется несколькими способами
Если множество содержит конечное число элементов и легко обозримо, оно может быть задано перечислением его элементов. Так, список лиц, входящих в некоторую учебную группу, задает множество студентов этой группы.
Запись означает, что множество состоит из трех элементов и

2. Множество может быть задано аналитически – посредством некоторого признака, присущего всем его и только его элементам. Например, фраза «множество целых чисел таких, что они делятся на 2» задает множество четных чисел. В математике множества часто задают формулами. Например, если – множество корней уравнения , то (читается: "множество состоит из всех элементов таких, что ").

3. Множество может быть задано алгоритмически – некоторым алгоритмом, порождающим из одних элементов множества другие его элементы. Например, множество всех натуральных чисел можно породить из числа 1 процедурой присоединения 1 к ранее уже построенному числу.

Другой пример алгоритмического задания множества.
Пусть M = {1, 2, 4, 8, 16,…} — множество степеней числа 2. Тогда его можно задать алгоритмом:
1) 1∈ М;
2) если x ∈ M, то 2x ∈ M.

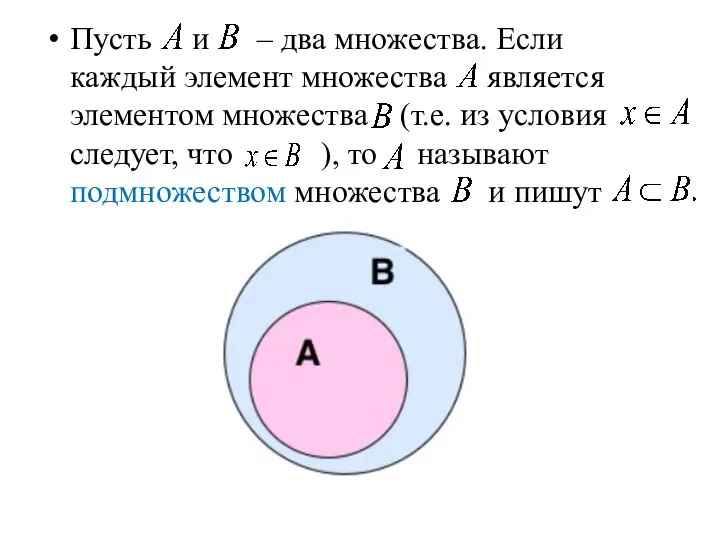
Пусть и – два множества. Если каждый элемент множества является элементом множества (т.е. из условия следует, что ), то называют подмножеством множества и пишут

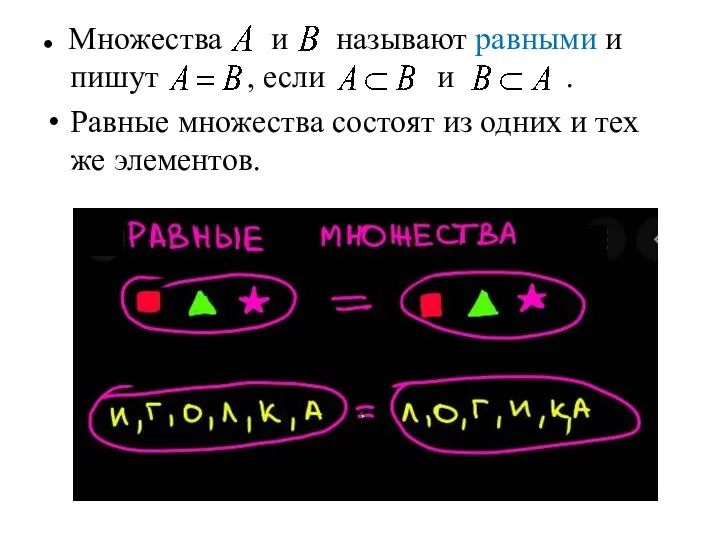
● Множества и называют равными и пишут , если и .
Равные множества состоят из одних и тех же элементов.

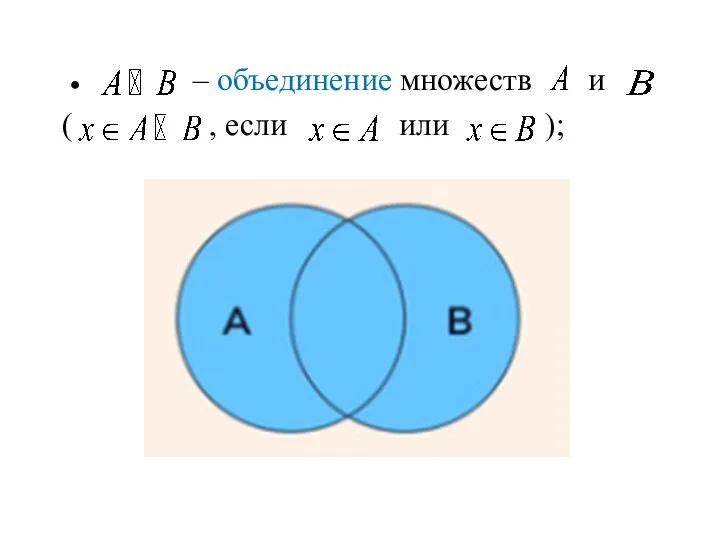
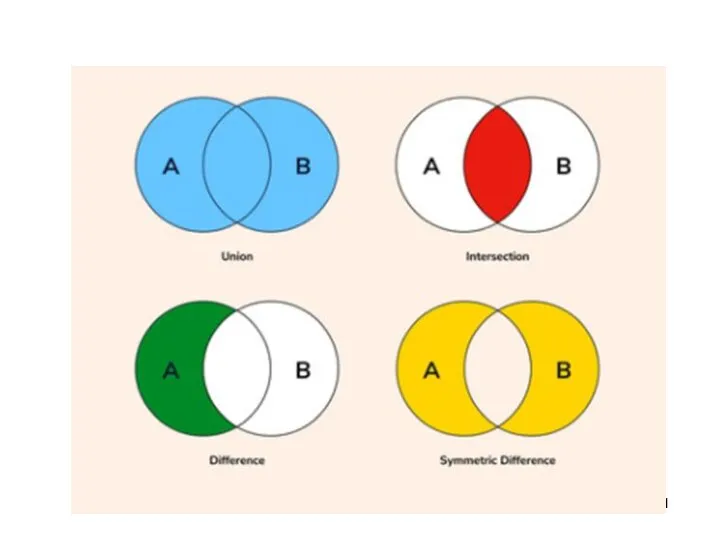
● – объединение множеств и
( , если или );

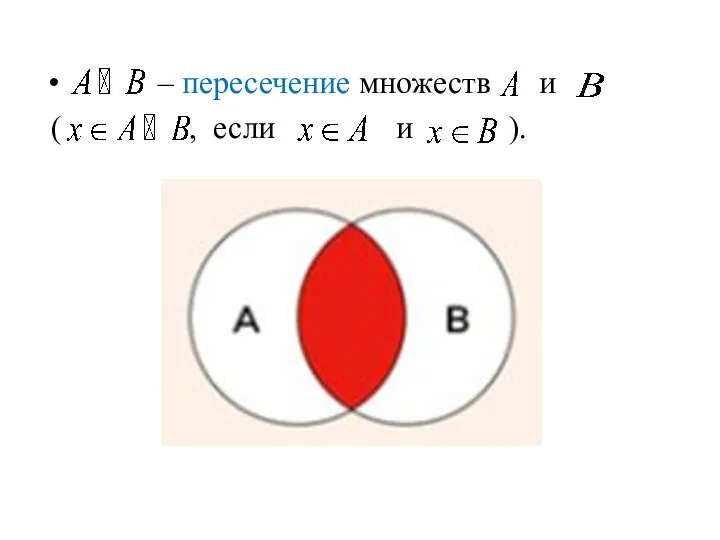
– пересечение множеств и
( , если и ).

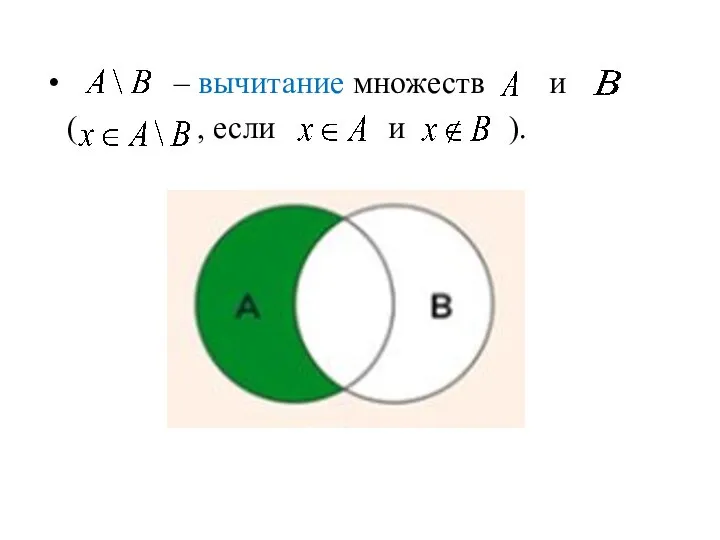
– вычитание множеств и
( , если и ).

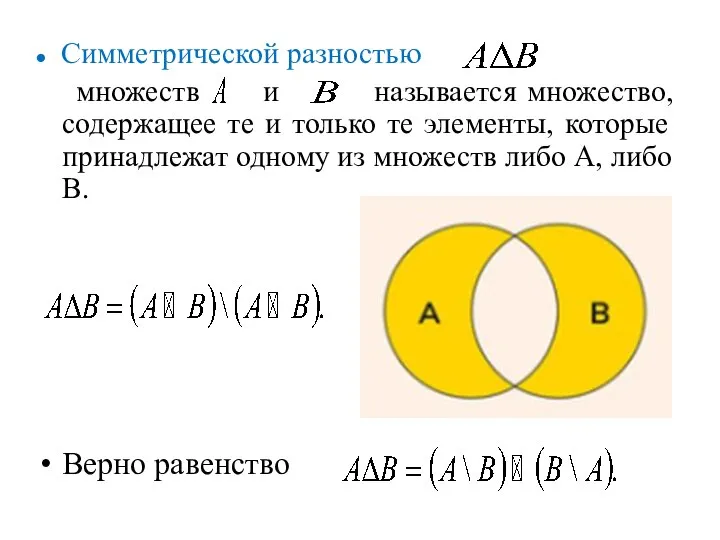
● Симметрической разностью
множеств и называется множество, содержащее те и только те элементы, которые принадлежат одному из множеств либо А, либо В.
Верно равенство

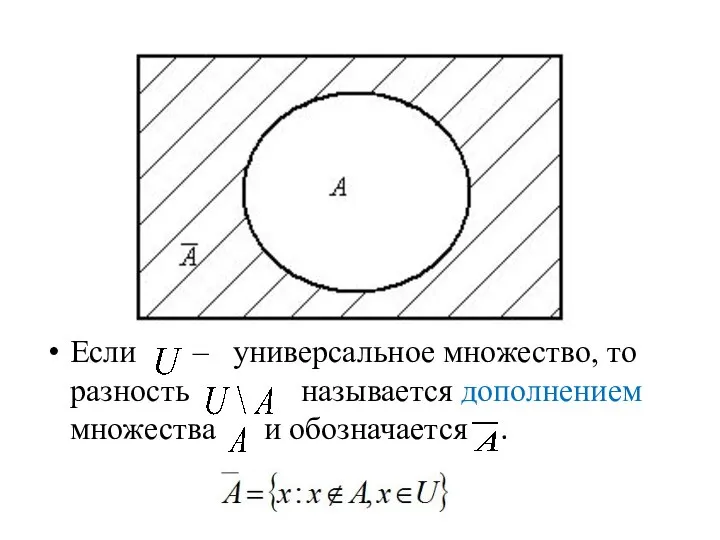
Если – универсальное множество, то разность называется дополнением множества и обозначается .

Декартово произведение множеств и обозначается и состоит из всех упорядоченных пар таких, что и .
Таким образом,

Пример. Даны множества
Найдите
Решение.
Вопрос:

Правило умножения
Если элемент x можно выбрать m способами,
а элемент y можно выбрать n способами, то
упорядоченную пару (x,y) можно выбрать
m n способами.
Иначе говоря, для любых конечных множеств
А и В верна формула

Правило сложения
Число элементов множества
находится по формуле
В частности, если множества А и В не
пересекаются, т.е. Ø, то

Пример. В группе из 27 студентов 17 пишут стихи, а 13 летают во сне. Трое студентов не умеют ни того, ни другого. Найдите число студентов, которые и стихи сочиняют и во сне летают.
Решение. По условию, хотя бы одним даром обладают 27 – 3 = 24 студента. Значит, только летают (а стихи не пишут) 24 – 17 = 7 чел., а 13 – 7 = 6 чел. и стихосложением занимаются и летают.

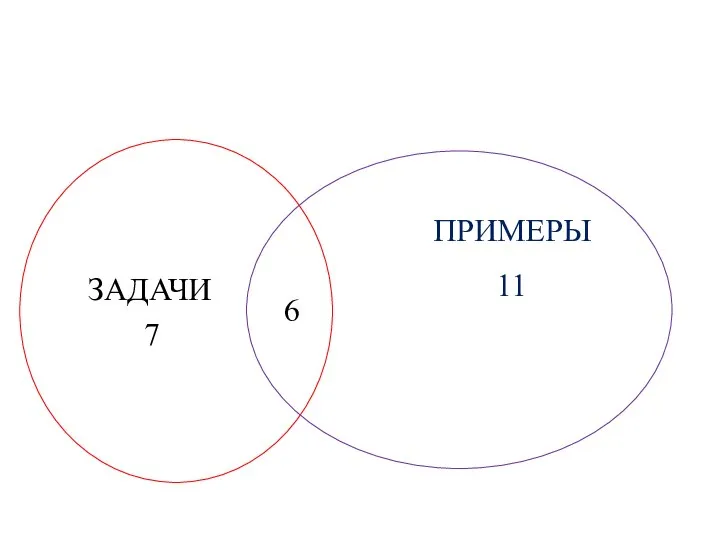
ЗАДАЧИ
7
ПРИМЕРЫ
11
6

Пример. Из 50 студентов курса 42 изучают английский язык, 31 – немецкий язык, а 25 – английский и немецкий языки. Сколько студентов курса не изучает ни английский, ни немецкий языки?
Решение. Пусть А – множество студентов курса, изучающих английский язык, B – множество студентов курса, изучающих немецкий язык, С – множество всех студентов курса. По условию задачи |А| = 42, |B| = 31, |А ⋂ B| = 25, |С| = 50.
Требуется найти число студентов курса, не изучающих ни английского, ни немецкого языка.

1 способ.
1) Найдем число элементов в объединении данных множеств. Для этого воспользуемся формулой правила сложения:
|А ∪ B|= |А| + |B| - |А ⋂ B| = 42 + 31 - 25 = 48.
2) Найдем число студентов курса, которые не изучают ни английский, ни немецкий языки: 50 - 48 = 2.

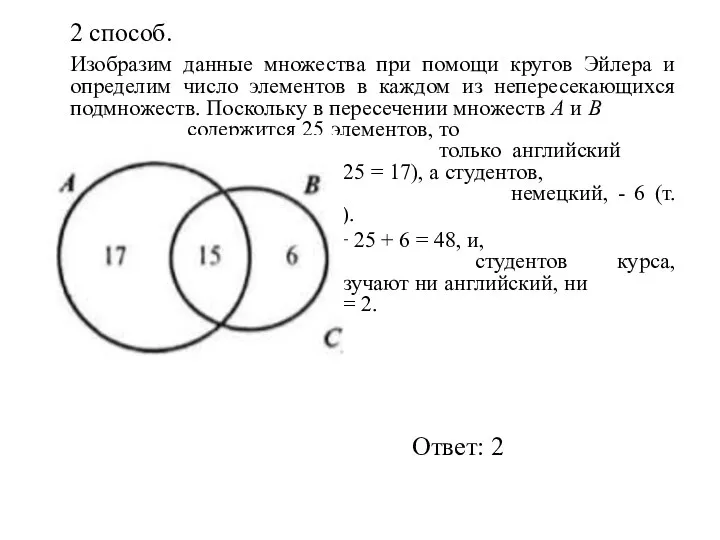
2 способ.
Изобразим данные множества при помощи кругов Эйлера и определим число элементов в каждом из непересекающихся подмножеств. Поскольку в пересечении множеств А и B содержится 25 элементов, то студентов изучающих только английский язык (42 - 25 = 17), а студентов, изучающих только немецкий, - 6 (т.к. 31 - 25 = 6).
|А∪B| = 17 + 25 + 6 = 48, и, следовательно, число студентов курса, которые не изучают ни английский, ни языки, будет 50 - 48 = 2.
Ответ: 2