Начертательная геометрия. Методы проецирования. (Лекция 1)

Начертательная геометрия (НГ) - это наука об изображении пространственных предметов на плоскости
В НГ пространственные предметы на плоскости изображаются с помощью методов проецирования.
Метод проекций – это метод отображения пространственных
фигур на плоскость.
Методы проецирования : центральное проецирование
параллельное проецирование
Аппарат проецирования – это направление проецирования и плоскость проекций.

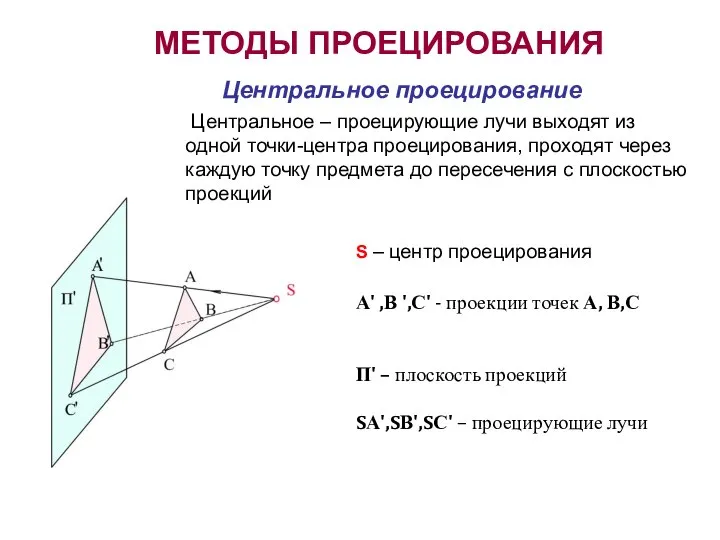
Центральное проецирование
МЕТОДЫ ПРОЕЦИРОВАНИЯ
S – центр проецирования
А' ,В ',С' - проекции точек А, В,С
П' – плоскость проекций
SА',SВ',SС' – проецирующие лучи
Центральное – проецирующие лучи выходят из одной точки-центра проецирования, проходят через каждую точку предмета до пересечения с плоскостью проекций

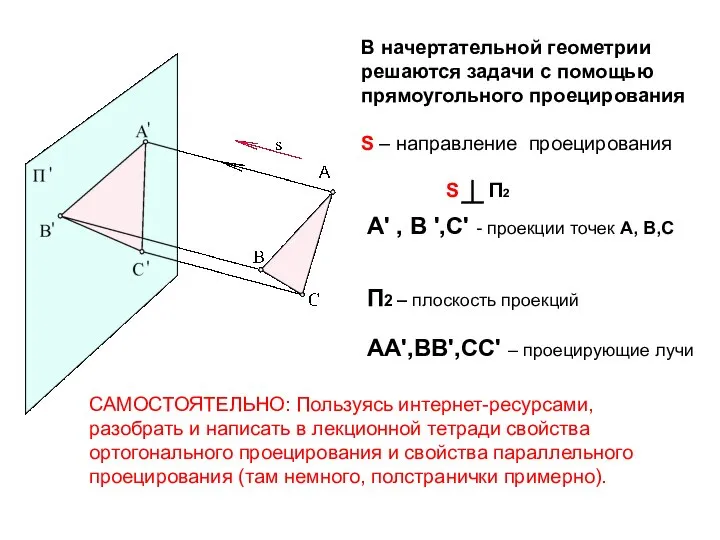
Параллельное проецирование
Параллельное проецирование – проецирование, при котором центр проецирования удален в бесконечность и проецирующие лучи становятся параллельны между собой. Оно делится на прямоугольное (или ортогональное) и косоугольное.
Параллельное косоугольное проецирование – это проецирование, при котором направление проецирования не перпендикулярно плоскости проекций. Проецирующие лучи параллельны между собой и не перпендикулярны плоскости проекций.
Параллельное прямоугольное (ортогональное) проецирование – это проецирование, при котором направление проецирования перпендикулярно плоскости проекций. Проецирующие лучи параллельны между собой и перпендикулярны плоскости проекций.

А' , В ',С' - проекции точек А, В,С
П2 – плоскость проекций
АА',ВВ',СС' – проецирующие лучи
В начертательной геометрии решаются задачи с помощью прямоугольного проецирования
S – направление проецирования
S
П2
САМОСТОЯТЕЛЬНО: Пользуясь интернет-ресурсами, разобрать и написать в лекционной тетради свойства ортогонального проецирования и свойства параллельного проецирования (там немного, полстранички примерно).

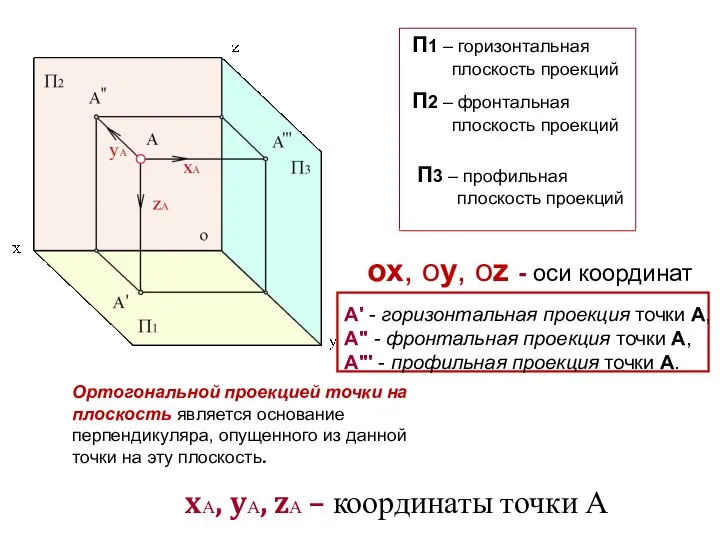
Проецирование точки

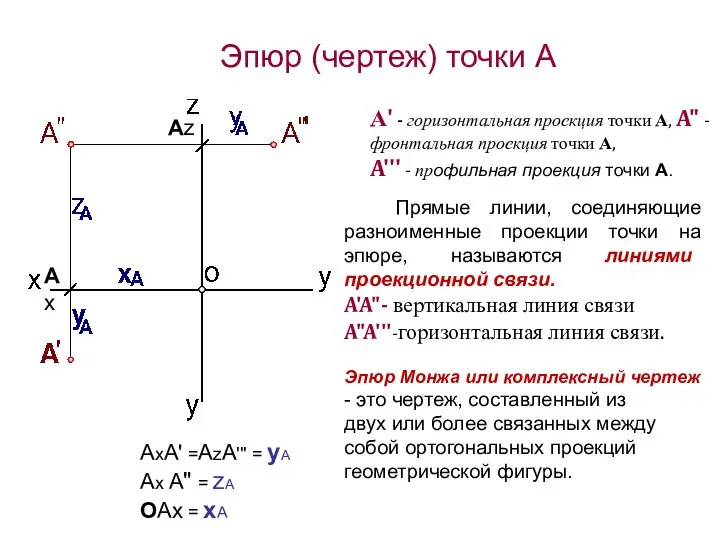
А' - горизонтальная проекция точки А,
A" - фронтальная проекция точки А,
A''' - профильная проекция точки А.
П1 – горизонтальная
плоскость проекций
П2 – фронтальная
плоскость проекций
П3 – профильная
плоскость проекций
оx, оy, оz - оси координат
xА, yА, zА – координаты точки А
Ортогональной проекцией точки на плоскость является основание перпендикуляра, опущенного из данной точки на эту плоскость.

Смотреть в полноэкранном режиме, показ слайдов, так как здесь анимация

Координаты точки
Определяют положение точки в пространстве.
Координата – это число определяющее расстояние от этой точки до соответствующей плоскостей проекций.
Записывается в виде - А (Х,У,Z)
Z – определяет расстояние от точки А до плоскости П1;
У – определяет расстояние от точки А до плоскости П2;
Х – определяет расстояние от точки А до плоскости П3.
координата Х (абсцисса), Y (ордината), Z (аппликата)

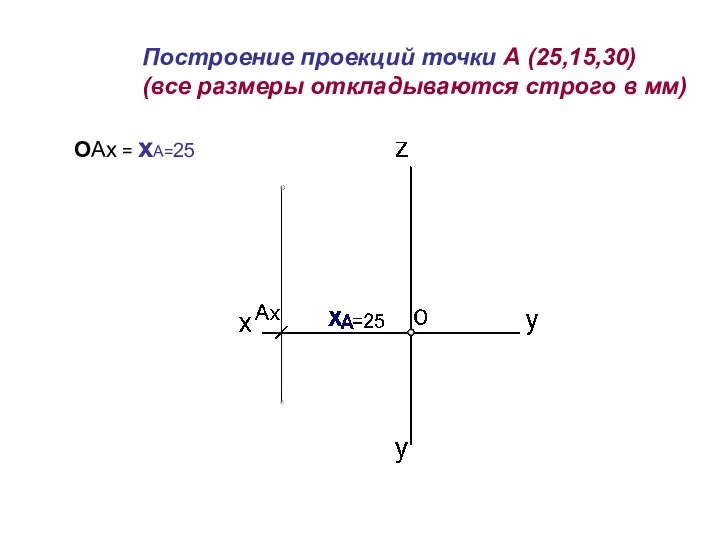
Построение проекций точки А (25,15,30)
(все размеры откладываются строго в мм)
ОAх = xА=25

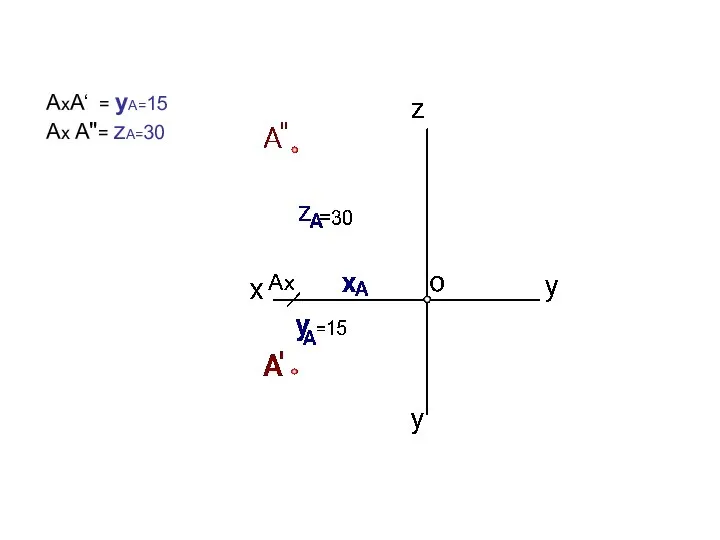
АхA‘ = yА=15
Aх A"= zА=30

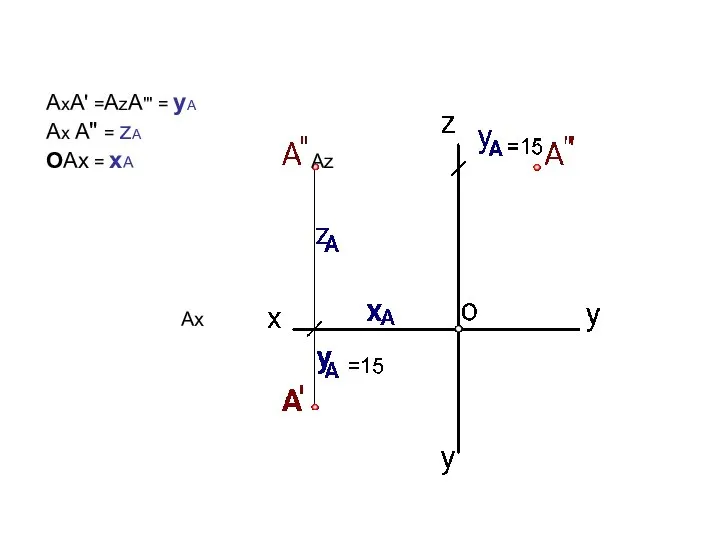
АхA' =АzA''' = yА
Aх A" = zА
ОAх = xА
Ах
Аz

Прямые линии, соединяющие разноименные проекции точки на эпюре, называются линиями проекционной связи.
A'A"- вертикальная линия связи
A"A'''-горизонтальная линия связи.
Эпюр Монжа или комплексный чертеж - это чертеж, составленный из
двух или более связанных между собой ортогональных проекций
геометрической фигуры.
А' - горизонтальная проекция точки А, A" - фронтальная проекция точки А,
A''' - профильная проекция точки А.
Ах
АхA' =АzA''' = yА
Aх A" = zА
ОAх = xА
Аz
Эпюр (чертеж) точки А

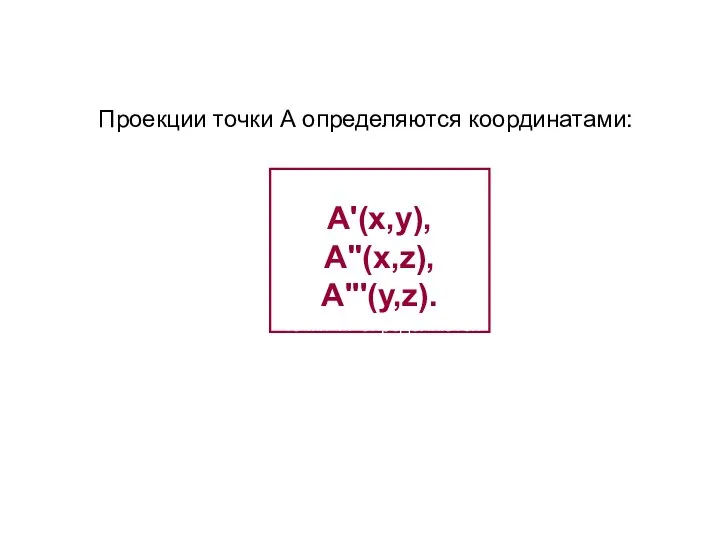
A'(x,y),
A"(x,z),
A'''(y,z).
точки А определяются координатами:
Проекции точки А определяются координатами:

Точки особого положения
Это точки, у которых одна, две или три координаты равны 0.

Одна координата равна 0
Х=0
А (0,У,Z) - точка лежит в П3
2. У=0 А (X,0,Z) - точка лежит в П2
3. Z=0
А (X,У,0)- точка лежит в П1

Две координаты равны 0
У, Z =0
А (X,0,0) - точка лежит на оси X
2. Х, Z=0
А (0, У,0) - точка лежит на оси У
3. X, У=0
А (0,0, Z)- точка лежит на оси Z

Три координаты равны 0
А(0,0,0)- точка лежит в начале координат
Если точка не занимает особое положение, значит она принадлежит одному из октантов.

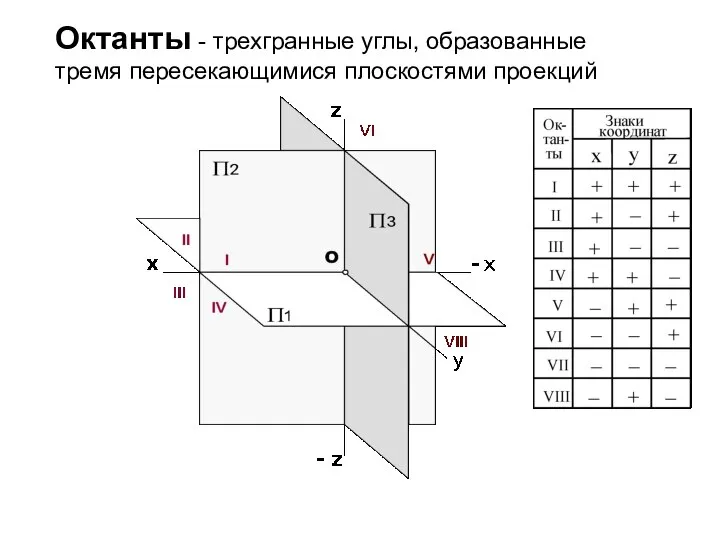
Октанты - трехгранные углы, образованные тремя пересекающимися плоскостями проекций

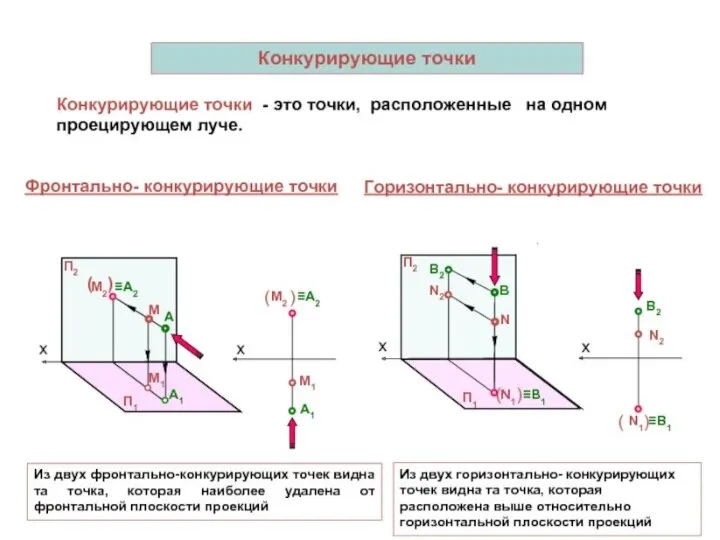
У профильно-конкурирующих точек совпадают профильные проекции. Видима будет та, которая расположена ближе к наблюдателю, стоящему лицом к профильной плоскости проекций, такая точка на наглядном изображении будет располагаться левее.
Видимость для совпадающих проекций конкурирующих точек также определяется сравнением координат этих точек в направлении общего проецирующего луча. Видима та проекция точки, у которой эта координата больше. При этом сравнение координат ведется на плоскости проекций с раздельными изображениями точек.

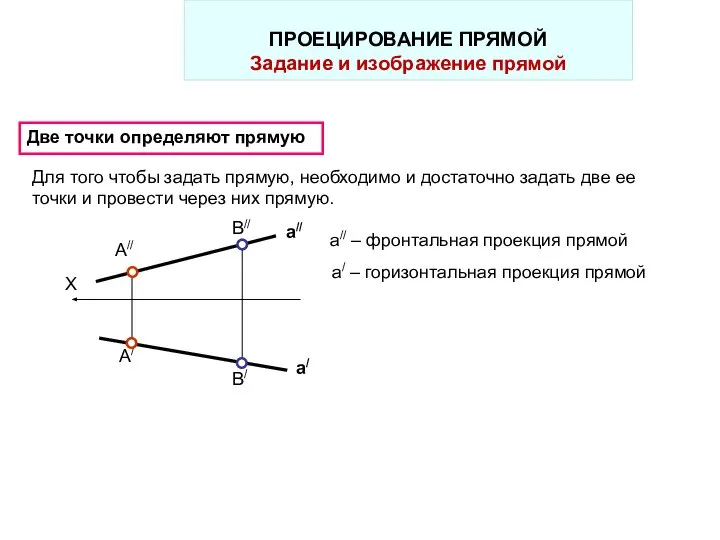
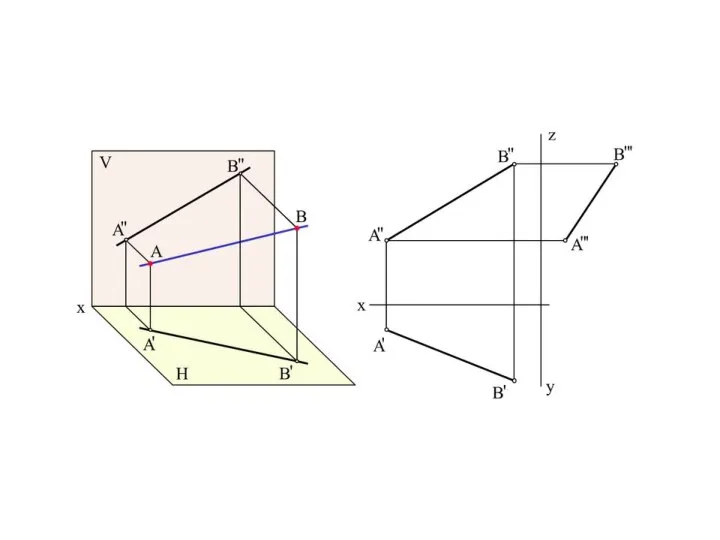
В/
В//
А/
Две точки определяют прямую
А//
X
Для того чтобы задать прямую, необходимо и достаточно задать две ее точки и провести через них прямую.
а//
а/
ПРОЕЦИРОВАНИЕ ПРЯМОЙ
Задание и изображение прямой
а// – фронтальная проекция прямой
а/ – горизонтальная проекция прямой

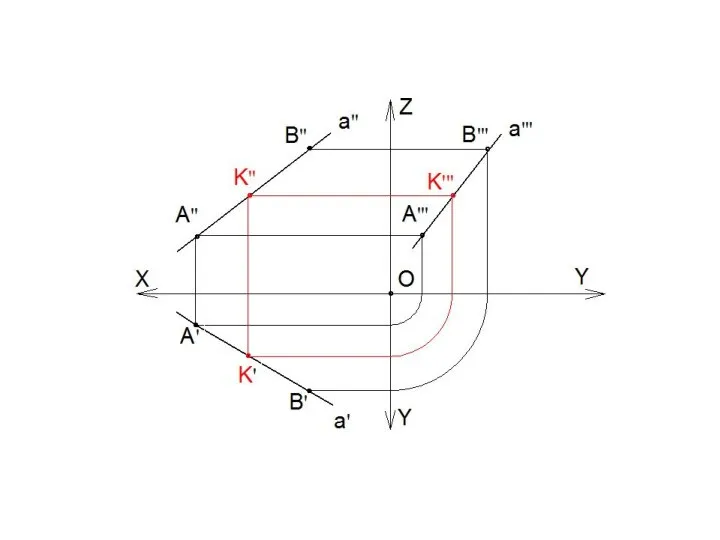
Относительное положение прямой и точки
Проекции точки, принадлежащей прямой, должны принадлежать соответствующим проекциям этой прямой
К∈a ⇨ K/∈a/
K//∈a //
K///∈a ///

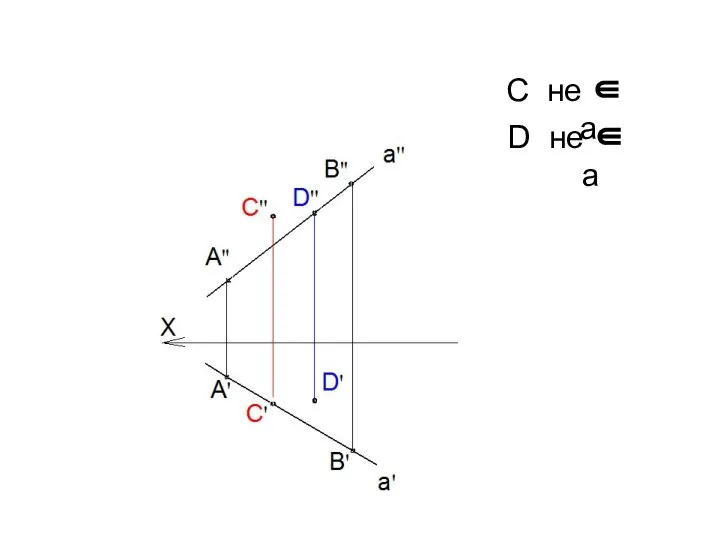
C не ∈ a
D не ∈ a

Отрезок прямой может занимать различное положение в пространстве относительно
плоскостей проекций (общее и частное).
Прямая общего положения – это прямая, не параллельная и не перпендикулярная, ни
одной из плоскостей проекций. Проекция этого отрезка на чертеже по величине всегда
меньше действительной величины прямой.