Слайд 2Степень с рациональным показателем
Действия со степенями

Слайд 3МОСКВА, 2009
ООО "РЕЗОЛЬВЕНТА"
Корень n − й степени
Любое решение уравнения
называется корнем n

– й степени из
числа b.
Слайд 4МОСКВА, 2009
ООО "РЕЗОЛЬВЕНТА"
Арифметический корень n − й степени
Неотрицательное решение уравнения
называется арифметическим

корнем
n – й степени из числа b.
Слайд 5МОСКВА, 2009
ООО "РЕЗОЛЬВЕНТА"
Обозначение арифметического корня
При n = 2 арифметический корень из

числа b обозначается
При n = 3, 4, … арифметический
корень из числа b обозначается
Слайд 6МОСКВА, 2009
ООО "РЕЗОЛЬВЕНТА"
Пример 1.

Слайд 7МОСКВА, 2009
ООО "РЕЗОЛЬВЕНТА"
Пример 2.

Слайд 8МОСКВА, 2009
ООО "РЕЗОЛЬВЕНТА"
Пример 3.

Слайд 9МОСКВА, 2009
ООО "РЕЗОЛЬВЕНТА"
Степень с рациональным показателем

Слайд 10МОСКВА, 2009
ООО "РЕЗОЛЬВЕНТА"
Степень с рациональным показателем (продолжение 1)

Слайд 11МОСКВА, 2009
ООО "РЕЗОЛЬВЕНТА"
Степень с рациональным показателем (продолжение 2)

Слайд 12МОСКВА, 2009
ООО "РЕЗОЛЬВЕНТА"
Запрещенные операции

Слайд 13МОСКВА, 2009
ООО "РЕЗОЛЬВЕНТА"
Модуль (абсолютная величина) числа

Слайд 14МОСКВА, 2009
ООО "РЕЗОЛЬВЕНТА"
Сравнение степеней с одним основанием

Слайд 15МОСКВА, 2009
ООО "РЕЗОЛЬВЕНТА"
График функции
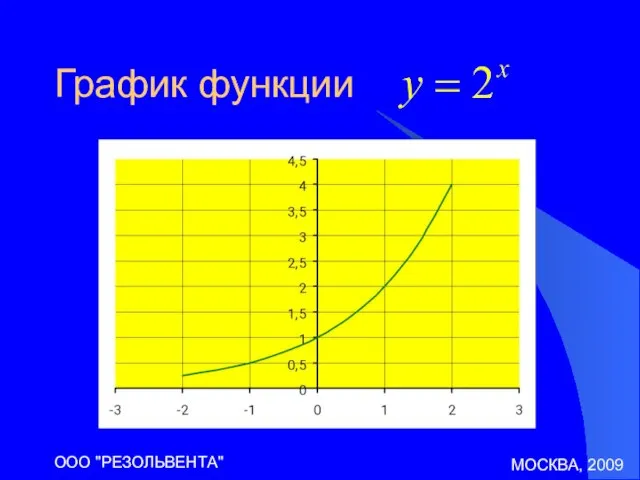
Слайд 16МОСКВА, 2009
ООО "РЕЗОЛЬВЕНТА"
График функции
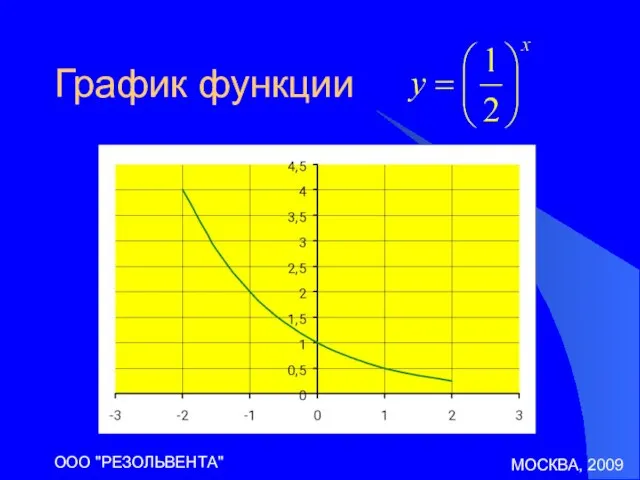















 Образы античной мифологии в мировой художественной культуре
Образы античной мифологии в мировой художественной культуре Весёлый гороскоп школьника
Весёлый гороскоп школьника Кодекс профессиональной этики педагога ФГАОУ Севастопольский государственный университет
Кодекс профессиональной этики педагога ФГАОУ Севастопольский государственный университет «Здоровая Еда»
«Здоровая Еда» Прославившиеся ученые Саратовской области
Прославившиеся ученые Саратовской области Proverbs and sayings
Proverbs and sayings «Поисковая оптимизация и продвижение сайтов в интернете-2005» Опыт системы «Бегун»: бюджетирование, динамика цен, определение эффек
«Поисковая оптимизация и продвижение сайтов в интернете-2005» Опыт системы «Бегун»: бюджетирование, динамика цен, определение эффек Презентация на тему Кометы
Презентация на тему Кометы «MEGAPOLUS TOURS»
«MEGAPOLUS TOURS» МБДОУ «Григорьевский детский сад» Зачем нужно чистить зубки?
МБДОУ «Григорьевский детский сад» Зачем нужно чистить зубки? Зачем люди осваивают космос
Зачем люди осваивают космос Организация как открытая система
Организация как открытая система Школьный музей "Родные истоки"
Школьный музей "Родные истоки" МОУ Айская средняя общеобразовательная школа
МОУ Айская средняя общеобразовательная школа Императоры Римской империи Династия Юлии-Клавдии Октавиан Август
Императоры Римской империи Династия Юлии-Клавдии Октавиан Август Детство и юность Н.И. Пирогова
Детство и юность Н.И. Пирогова Прогимназия № 698 Московского района СПб Пансион
Прогимназия № 698 Московского района СПб Пансион Презентация на тему Взаимные превращения жидкости, пара и твёрдого тела
Презентация на тему Взаимные превращения жидкости, пара и твёрдого тела Содержание
Содержание Понятие государства и его признаки
Понятие государства и его признаки Сучасна Скульптура
Сучасна Скульптура Развитие социальной уверенности у дошкольников
Развитие социальной уверенности у дошкольников Функции управления
Функции управления Поговорим о дисциплине
Поговорим о дисциплине МЕМОРИАЛЬНЫЙ МУЗЕЙ ИСТОРИИ
МЕМОРИАЛЬНЫЙ МУЗЕЙ ИСТОРИИ Атмосфера: значение, строение, изучение
Атмосфера: значение, строение, изучение Презентация на тему Вооруженные Силы Российской Федерации
Презентация на тему Вооруженные Силы Российской Федерации Астанинская Ассоциация Выпускников:отчет за 2010 и планы на 2011
Астанинская Ассоциация Выпускников:отчет за 2010 и планы на 2011