Содержание
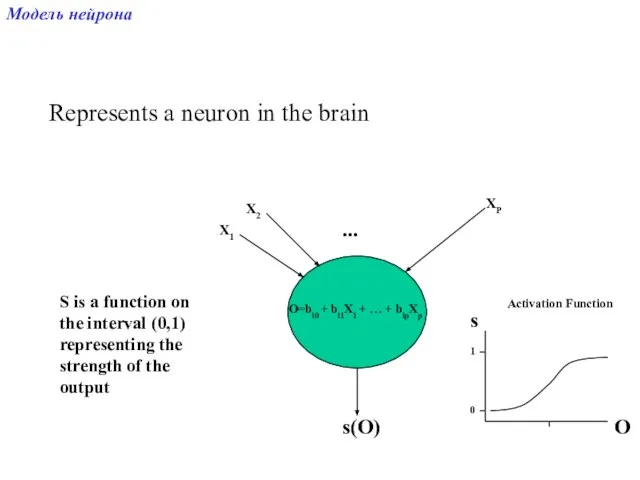
- 2. Represents a neuron in the brain X1 X2 XP ... O=bi0 + bi1X1 + … +
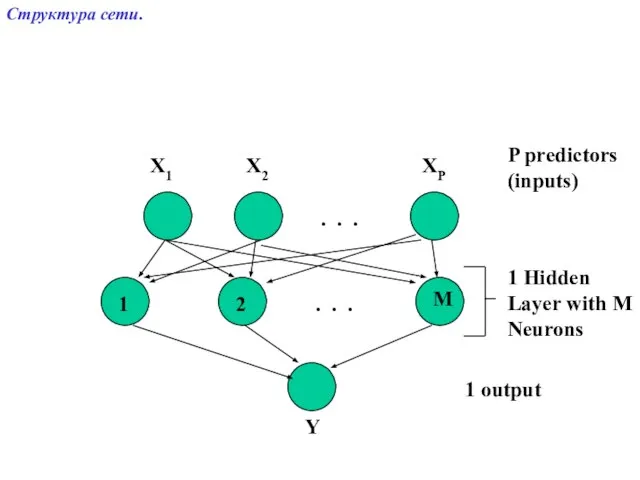
- 3. . . . . . . X1 X2 XP Y P predictors (inputs) 1 Hidden Layer
- 4. Принципиальная особенность сетей – необходимость их обучения для решения каждой конкретной задачи. Обучение. Задаётся обучающее множество
- 5. Диссертация посвящена разработке инструментария и техники для диагностики нейтронов и анализа данных, полученных при изучении термоядерных
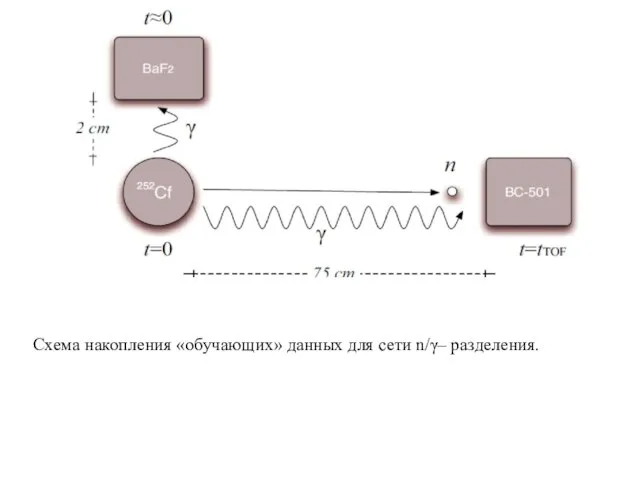
- 6. Схема накопления «обучающих» данных для сети n/γ– разделения.
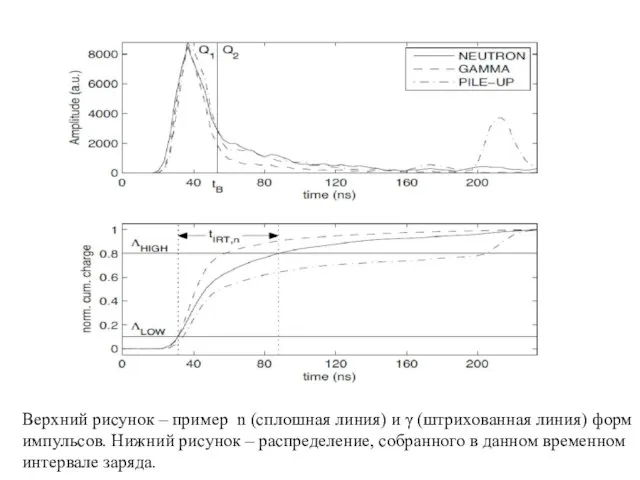
- 7. Верхний рисунок – пример n (сплошная линия) и γ (штрихованная линия) форм импульсов. Нижний рисунок –
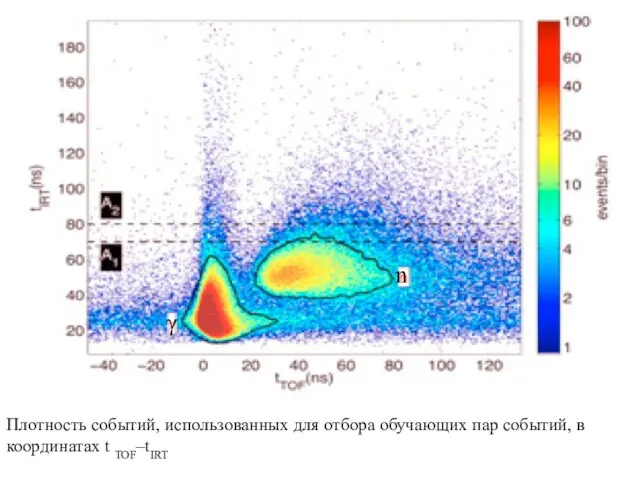
- 8. Плотность событий, использованных для отбора обучающих пар событий, в координатах t TOF–tIRT γ n
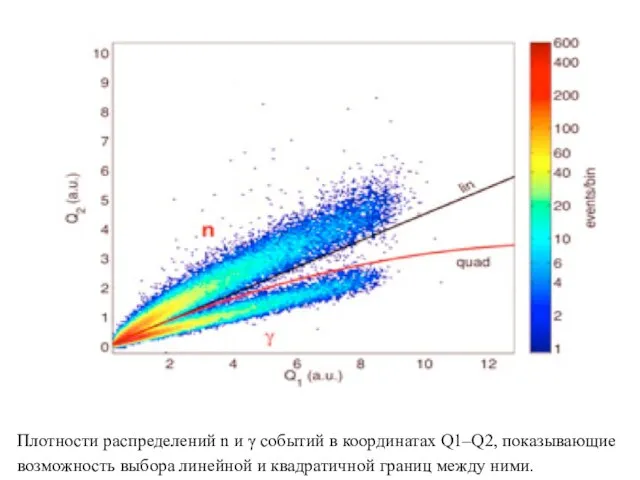
- 9. Плотности распределений n и γ событий в координатах Q1–Q2, показывающие возможность выбора линейной и квадратичной границ
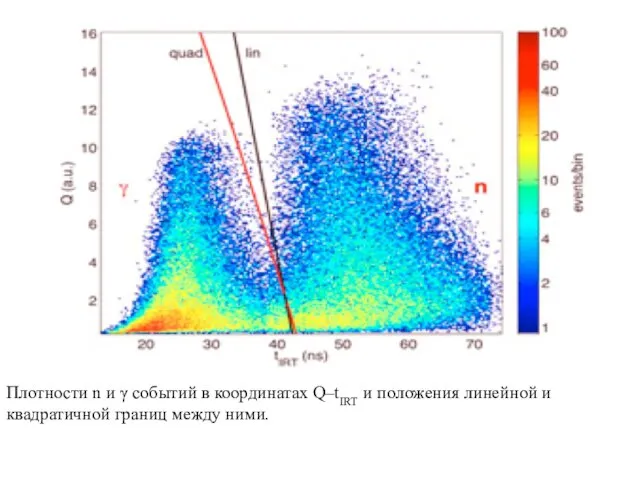
- 10. Плотности n и γ событий в координатах Q–tIRT и положения линейной и квадратичной границ между ними.
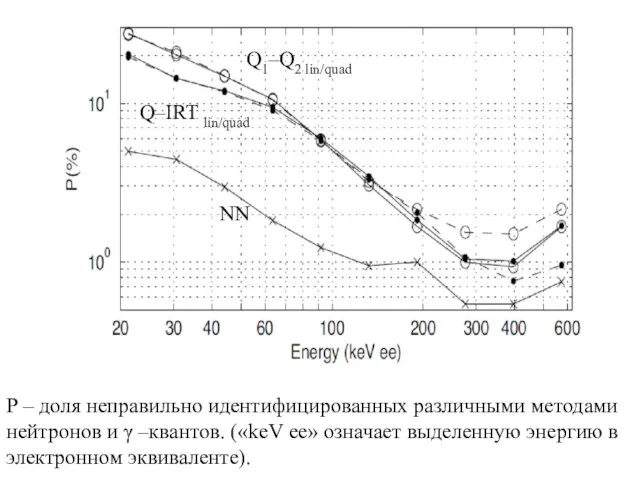
- 11. Р – доля неправильно идентифицированных различными методами нейтронов и γ –квантов. («keV ee» означает выделенную энергию
- 12. Архитектура нейронной сети, использованной для классификации n/γ–событий была «feed-forward» распространения с 71 входными нейронами (~ 200
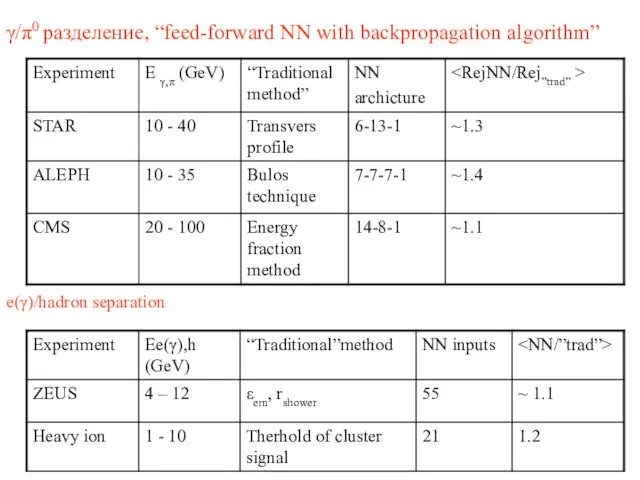
- 14. γ/π0 разделение, “feed-forward NN with backpropagation algorithm” e(γ)/hadron separation
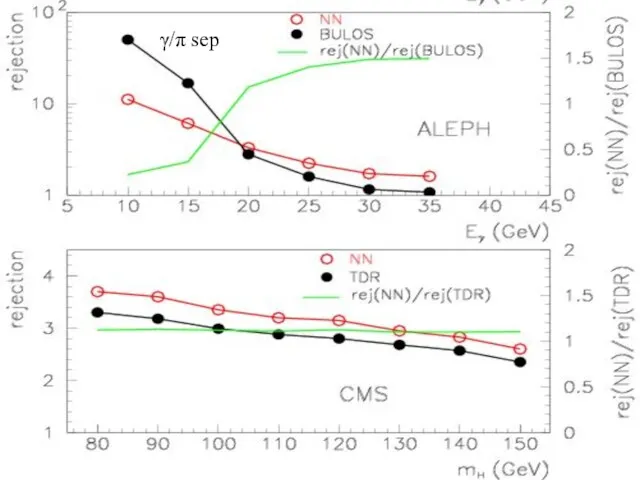
- 15. γ/π sep
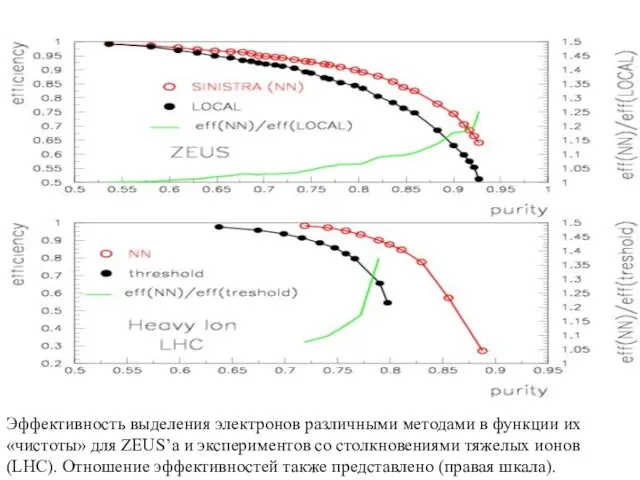
- 16. Эффективность выделения электронов различными методами в функции их «чистоты» для ZEUS’a и экспериментов со столкновениями тяжелых
- 17. Идентификация адронов в DELPHI основана на информации от RICH спектрометра и dE/dx информации от Time Projection
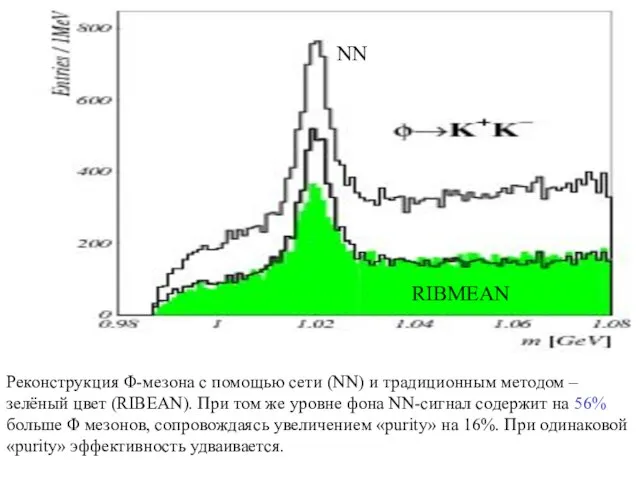
- 18. Реконструкция Φ-мезона с помощью сети (NN) и традиционным методом –зелёный цвет (RIBEAN). При том же уровне
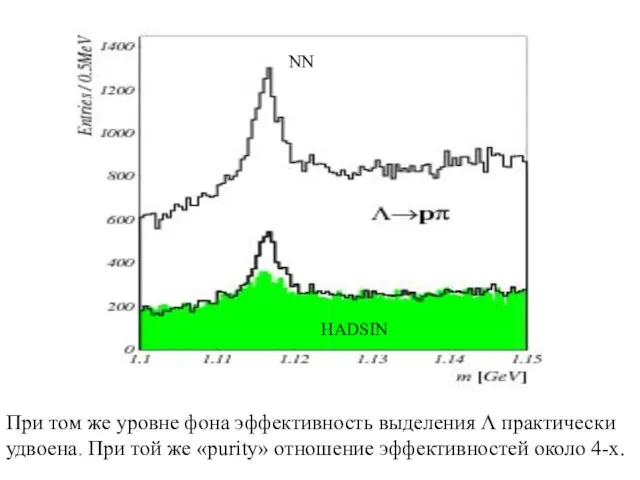
- 19. NN HADSIN При том же уровне фона эффективность выделения Λ практически удвоена. При той же «purity»
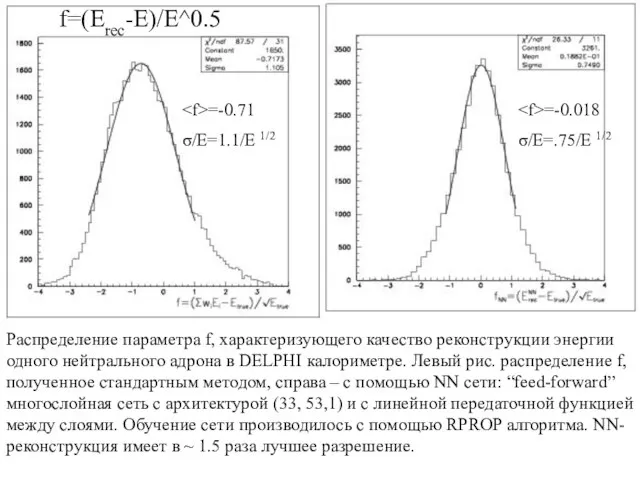
- 20. Распределение параметра f, характеризующего качество реконструкции энергии одного нейтрального адрона в DELPHI калориметре. Левый рис. распределение
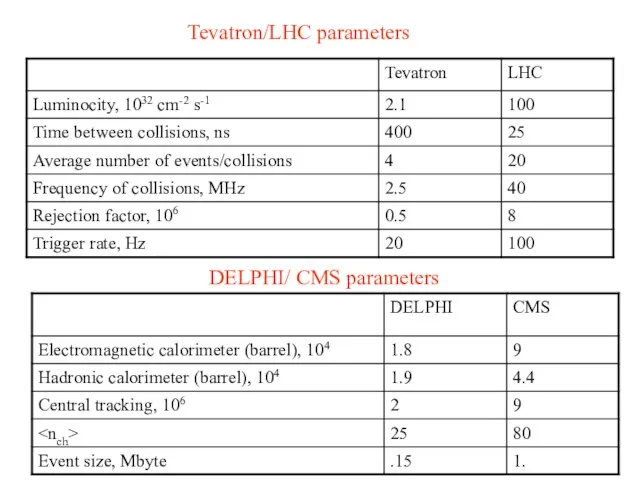
- 21. Tevatron/LHC parameters DELPHI/ CMS parameters
- 22. Заключение: Бόльшие энергии следующего поколения ускорителей (LHC), скорости счета событий, множественности будут иметь следствием , что
- 23. Application of Neural Networks Optimized by Genetic Algorithms to Higgs Boson Search František Hakl, Marek Hlaváček,
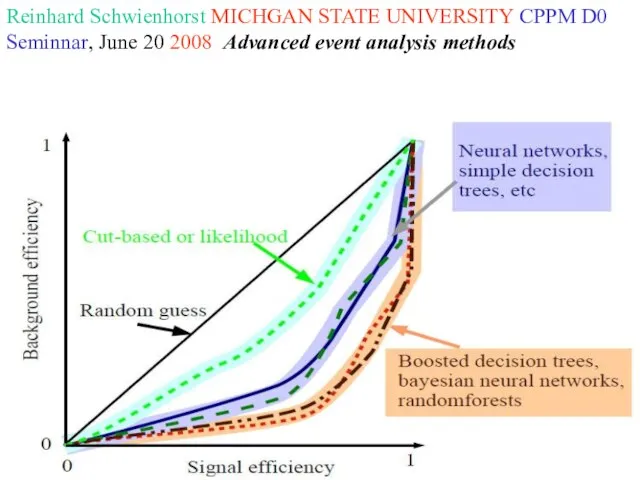
- 25. Reinhard Schwienhorst MICHGAN STATE UNIVERSITY CPPM D0 Seminnar, June 20 2008 Advanced event analysis methods
- 27. Скачать презентацию








 Российский государственный архив литературы и искусства (РГАЛИ)
Российский государственный архив литературы и искусства (РГАЛИ) Программа 2021-2022 по работе с вузами. Банковская школа
Программа 2021-2022 по работе с вузами. Банковская школа .
. Fibo Musang Elite
Fibo Musang Elite Рисуем по координатам
Рисуем по координатам Безигольная мезотерапия Откройте для себя здоровую, юную кожу
Безигольная мезотерапия Откройте для себя здоровую, юную кожу Презентация на тему Древний Рим Римская империя
Презентация на тему Древний Рим Римская империя  Русские имена в географических названиях на карте мира
Русские имена в географических названиях на карте мира Картины художников стиля рококо
Картины художников стиля рококо Сахарный диабет
Сахарный диабет  Презентация на тему Растворение. Растворы (8 класс)
Презентация на тему Растворение. Растворы (8 класс) Презентация на тему Сказка о рыбаке и рыбке
Презентация на тему Сказка о рыбаке и рыбке Антисциентизм всовременном мире
Антисциентизм всовременном мире Ответы квиз-плиз
Ответы квиз-плиз О вреде курения
О вреде курения Процесс балансировки шлифовальных кругов
Процесс балансировки шлифовальных кругов Презентация на тему Произведения Саши Чёрного для детей
Презентация на тему Произведения Саши Чёрного для детей 5-я ежегодная конференция по схематизации “Схематизация в мышлении, деятельности, рефлексии” Москва, 2 июня 2011 г.Вячеслав Мара
5-я ежегодная конференция по схематизации “Схематизация в мышлении, деятельности, рефлексии” Москва, 2 июня 2011 г.Вячеслав Мара ВИРТУАЛЬНЫЙ УДАЛЕННЫЙ ЛАБОРАТОРНЫЙ ПРАКТИКУМ ПО РОБОТОТЕХНИКЕ Зимин А.М., Илларионов В.В., Лесков А.Г., Лескова С.М., Шумов А.В.Мо
ВИРТУАЛЬНЫЙ УДАЛЕННЫЙ ЛАБОРАТОРНЫЙ ПРАКТИКУМ ПО РОБОТОТЕХНИКЕ Зимин А.М., Илларионов В.В., Лесков А.Г., Лескова С.М., Шумов А.В.Мо Загадка
Загадка Inclusion – включение (80-е годы XX века).)
Inclusion – включение (80-е годы XX века).) Археологічна інформаційна система
Археологічна інформаційна система Сборы ПМ РЦ Юг
Сборы ПМ РЦ Юг Компания Литани
Компания Литани "Природы храм" выполнил выпускник ОУ Черняевской МСОШ Щиров Дмитрий рук. Щирова Е.В.
"Природы храм" выполнил выпускник ОУ Черняевской МСОШ Щиров Дмитрий рук. Щирова Е.В. Пластический обмен. Синтез белка
Пластический обмен. Синтез белка Федеральное государственное бюджетное учреждение «Дом отдыха «ТУАПСЕ»
Федеральное государственное бюджетное учреждение «Дом отдыха «ТУАПСЕ» природні явища
природні явища