Некоторые матричные операции в MS Excel

Диапазон – это совокупность смежных ячеек, образующих прямоугольную область таблицы, заданную адресами левой верхней и нижней правой ячеек области. При указании диапазона принята форма записи, в которой эти адреса указываются через двоеточие.
B2:D4 – это диапазон из девяти ячеек B2, B3, B4, C2, C3, C4, D2, D3, D4 (матрица размера 3х3);
B2:B5 - это диапазон из четырех ячеек B2, B3, B4, B5 (вектор- столбец);
B2:E2 - это диапазон из четырех ячеек B2, C2, D2, E2 (вектор-строка)

формулы массива
В MS Excel возможен ввод формул, результатом которых является не одно число, а диапазон чисел – это так называемые (в документации по программе) формулы массива.
Для ввода таки формул необходимо выполнить следующие действия:
Выделить ячейки, в которые должен быть помещен результат выполнения формулы.
Ввести формулу массива
нажать комбинацию клавиш Ctrl+Shift+Enter для завершения ввода (для этого нажимаются и удерживаются клавиши Ctrl+Shift и затем кратковременно нажимается клавиша Enter).
Введенные формулы массива отображаются в строке формул в фигурных скобках.

формулы массива
Для изменения (или удаления) введенной ранее формулы массива необходимо предварительно выделить весь диапазон ячеек, этой формулы, а затем выполнить желаемое действие. Часть ячеек формулы массива изменить нельзя.

Операции с векторами и матрицами
Результат сложения (вычитания) матриц (векторов) одинакового размера n x m (A) и (B) (число столбцов и строк матриц должны совпадать) есть матрица (C) размера n x m, каждый элемент которой равен сумме (или разности) соответствующих элементов матиц (A) и (B) .

Скалярное произведение двух векторов.
Скалярным произведением двух векторов одинаковой длины n называется сумма парных произведений соответствующих компонентов вектора.
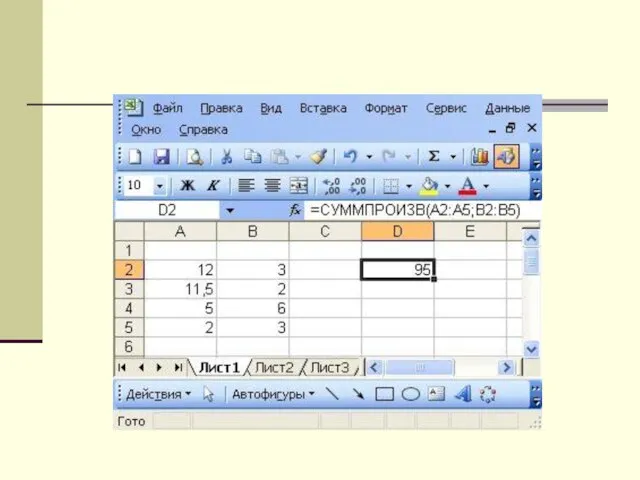
Для этой операции можно использовать встроенную функцию СУММПРОИЗВ.

Матричное произведение
Произведением матриц (A) размером n x m и (B) размером m x l называется матрица (C) размером n x l , такая что элемент, стоящий на пересечении i-ой строки и j-го столбца cij равен скалярному произведению i-ой строки матрицы (A) и j-ого столбца матрицы (B).

Матричное произведение
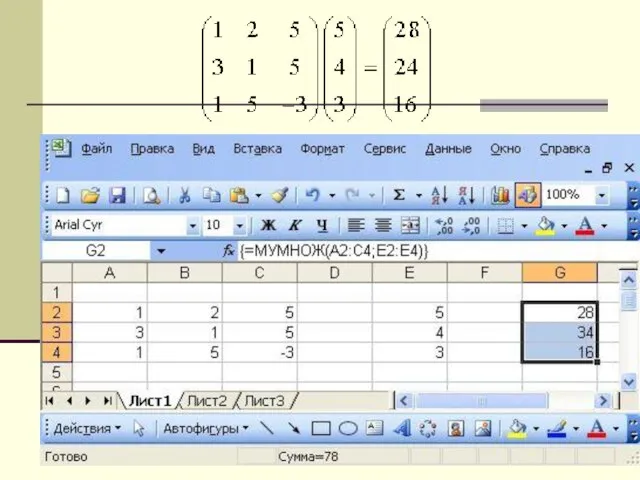
В MS Excel для матричного умножения исполдьзуется встроенная функция МУМНОЖ. У нее два параметра, соответствующих двум диапазонам, содержащим перемножаемые матрицы. Результат функции - это матрица, поэтому вводиться она должна в диапазон ячеек как функция массива.

Обращение матрицы
Матрицей, обратной матрице (А) размера (n x n) называется такая матрица (А)-1 размера (n x n), что при перемножении этих матриц в любом порядке получается единичная диагональная матрица:
здесь (1) – это единичная диагональная матрица размера (n x n) – все элементы которой равны 0, за исключением диагональных, которые равны 1.

Обращение матрицы
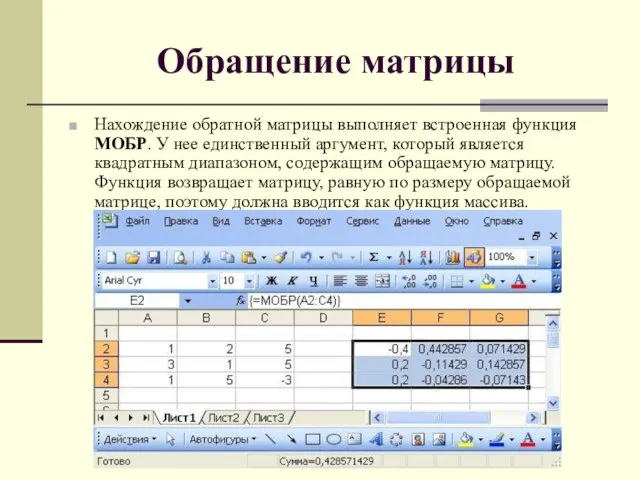
Нахождение обратной матрицы выполняет встроенная функция МОБР. У нее единственный аргумент, который является квадратным диапазоном, содержащим обращаемую матрицу. Функция возвращает матрицу, равную по размеру обращаемой матрице, поэтому должна вводится как функция массива.