Содержание
- 2. Ниже будем использовать следующие обозначения: катеты и гипотенуза прямоугольного треугольника ABC соответственно a, b и c
- 3. Теорема Пифагора и подобие фигур для n - мерного пространства Будем считать F1 подобной F2 в
- 4. Теорема 1 и теорема 2 для двухмерного пространства Т1. Если F1 подобна F3, где k=a/c=sin A,
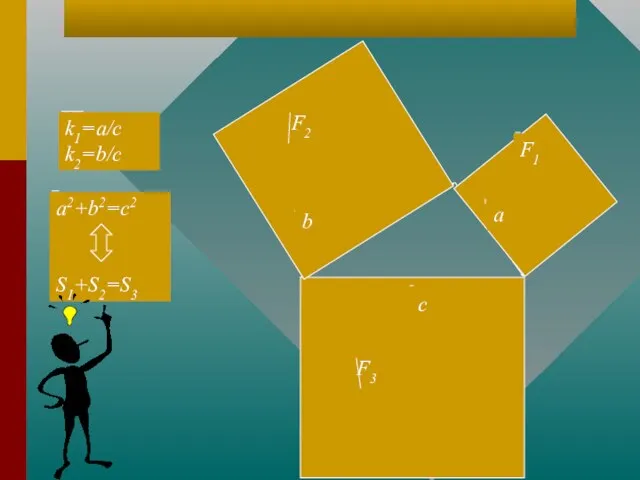
- 5. а b c F1 F2 F3 a2+b2=c2 S1+S2=S3 k1=a/c k2=b/c Иллюстрация к теоремам 1 и 2
- 6. Доказательство Т 1 Из подобия фигур следует равенство : S1+S2 =S3(a2+b2)/c2 (см.доказательствоТ2). По условию S1+S2=S3 ,
- 7. Доказательство Т2 Из подобия фигур, отношение площадей которых равно квадрату коэффициента подобия, следует : S1= (a2/c2)S3
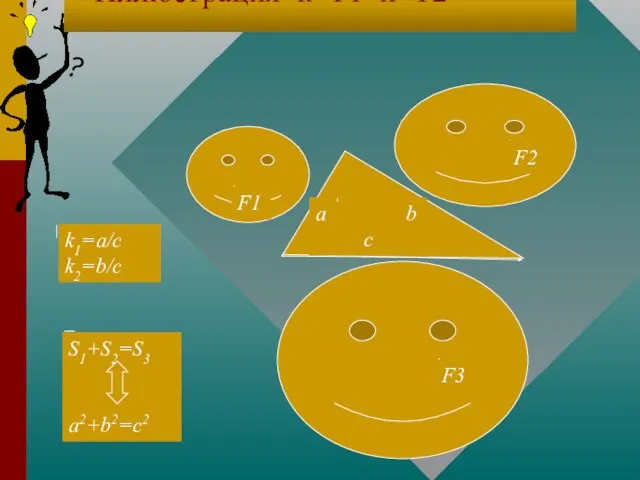
- 8. F2 F1 F3 a b c S1+S2=S3 a2+b2=c2 k1=a/c k2=b/c Иллюстрация к Т1 и Т2
- 9. Теорема 3 и теорема 4 для трехмерного пространства Т3. Если F1 подобна F3, где k=3V¯(a/c)2, F2
- 10. Доказательство Т3 и Т4. Отношение объемов подобных фигур равно кубу коэффициента подобия, поэтому V1=(а2/c2)V3 и V2=(b2/c2)V3
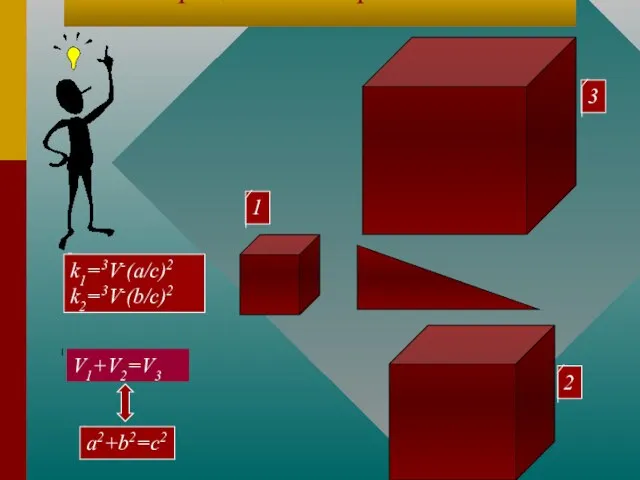
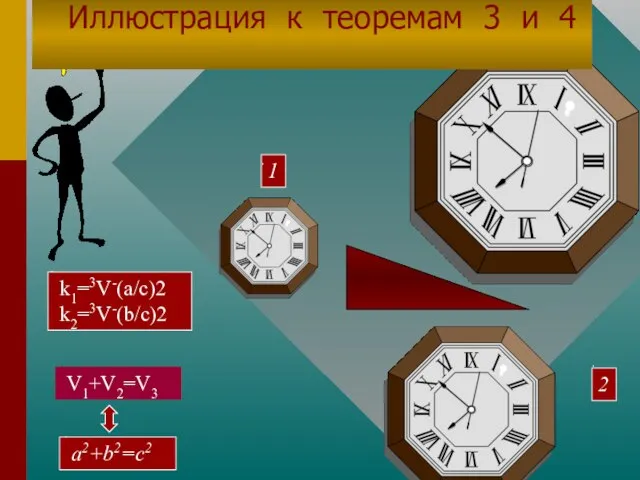
- 11. V1+V2=V3 a2+b2=c2 k1=3V-(a/c)2 k2=3V-(b/c)2 1 3 2 Иллюстрация к теоремам 3 и 4
- 12. V1+V2=V3 a2+b2=c2 k1=3V-(a/c)2 k2=3V-(b/c)2 1 3 2 Иллюстрация к теоремам 3 и 4
- 13. Теоремы 5 и 6 для одномерного пространства Т5. Если F1 подобна F3, где к=а2/с2, F2 подобна
- 15. Скачать презентацию








 Оздоровительная работа в МКДОУ детский сад № 4
Оздоровительная работа в МКДОУ детский сад № 4 Искусство во имя Победы
Искусство во имя Победы Авиационные заводы и высшее военное авиационное училище в Узбекистане
Авиационные заводы и высшее военное авиационное училище в Узбекистане Достопримечательности Калининграда
Достопримечательности Калининграда Презентация на тему Наследственная изменчивость
Презентация на тему Наследственная изменчивость Ринок-“невидимка” – реклама в b2b пресі
Ринок-“невидимка” – реклама в b2b пресі Информационные технологии как фактор развития бизнеса
Информационные технологии как фактор развития бизнеса АЦТЕКИ Выполнили: Кузь Кристина Мардер Семен Кузнецова Екатерина Гуселетова Дарья Макрушевский Владимир Шемятихин Максим
АЦТЕКИ Выполнили: Кузь Кристина Мардер Семен Кузнецова Екатерина Гуселетова Дарья Макрушевский Владимир Шемятихин Максим  Пермский государственный технический университет Система дистанционного обучения. Организация, методология и анализ опыта
Пермский государственный технический университет Система дистанционного обучения. Организация, методология и анализ опыта Твоя профессиональная карьера
Твоя профессиональная карьера По волнам памяти
По волнам памяти Подобие треугольников. Первый признак подобия
Подобие треугольников. Первый признак подобия Формирование комфортной городской среды
Формирование комфортной городской среды великие просветители Европы
великие просветители Европы Системно-деятельностный подход является объединением системного подхода, который разрабатывался в исследованиях классиков наше
Системно-деятельностный подход является объединением системного подхода, который разрабатывался в исследованиях классиков наше Что такое Интранет: Интранет сайт (интранет система) - это система, использующая в своей основе Интернет технологии. Данная система
Что такое Интранет: Интранет сайт (интранет система) - это система, использующая в своей основе Интернет технологии. Данная система  Ты в наших поступках, ты в наших мыслях
Ты в наших поступках, ты в наших мыслях Примерная структура каждого типа урока по ФГОС
Примерная структура каждого типа урока по ФГОС Основы самоорганизации и эффективного взаимодействия ТЕХНОЛОГИИ САМООРГАНИЗАЦИИ
Основы самоорганизации и эффективного взаимодействия ТЕХНОЛОГИИ САМООРГАНИЗАЦИИ РАНХиГС_очно_27.09.2022_Акцнт, реф, защ, техн ОС
РАНХиГС_очно_27.09.2022_Акцнт, реф, защ, техн ОС Литьё из гипса. Подсвечник из листьев
Литьё из гипса. Подсвечник из листьев Что такое прокуратура
Что такое прокуратура Les impressionnistes
Les impressionnistes Разделительные Ь и Ъ знаки
Разделительные Ь и Ъ знаки Презентация на тему Рекомендации по написанию исследовательских работ
Презентация на тему Рекомендации по написанию исследовательских работ Мыло
Мыло Боевые искусства Древней Руси
Боевые искусства Древней Руси Презентация на тему Выборы в демократическом обществе.
Презентация на тему Выборы в демократическом обществе.