Непараметрические критерии. Частотный анализ

Особенности выборки, необходимые для проведения параметрических тестов
Случайность измерений (randomness)
Независимость измерений (independence)
Гомогенность дисперсии (homogeneity = homoscedasticity)
Соответствие нормальному распределению
Для факторной ANOVA – аддитивность (пояснить с табличкой)
Повторение из предыдущих занятий
Трансформация данных

Параметрические тесты:
нулевая гипотеза формулируется о конкретных ПАРАМЕТРАХ РАСПРЕДЕЛЕНИЯ и/или эти параметры входят в формулу статистики критерия.
Параметры: среднее значение, стандартное отклонение, дисперсия…
Почему при проведении параметрических тестов важно соблюдать условия?
Нарушим условие соответствия выборки нормальному распределению и проведём одновыборочный t-тест!
Трансформация данных

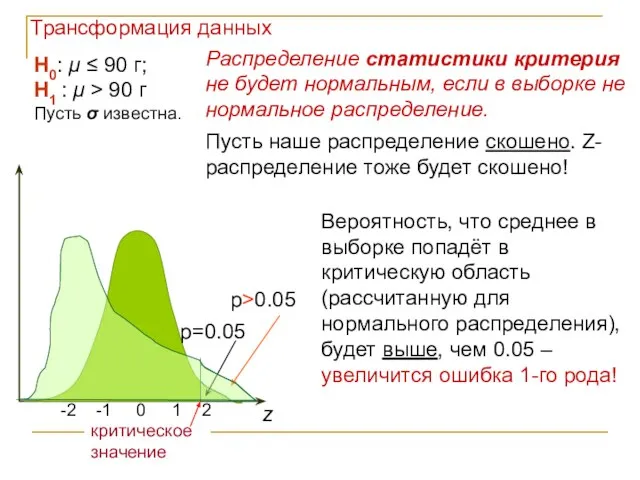
H0: μ ≤ 90 г;
H1 : μ > 90 г
Пусть σ известна.
Распределение статистики критерия не будет нормальным, если в выборке не нормальное распределение.
Пусть наше распределение скошено. Z-распределение тоже будет скошено!
z
р=0.05
0
1
2
-1
-2
р>0.05
критическое значение
Вероятность, что среднее в выборке попадёт в критическую область (рассчитанную для нормального распределения), будет выше, чем 0.05 – увеличится ошибка 1-го рода!
Трансформация данных

Основной вывод:
пренебрежения условиями использования параметрических тестов может увеличивать ошибку 1-го рода.
(Неизвестно, насколько)
Примечание: слабые отклонения от нормального распределения не очень страшны (в силу Центральной предельной теоремы), а для больших выборок ими можно пренебречь.
ANOVA устойчива к отклонениям от нормального распределения, особенно если выборки одинаковы по размеру.
Трансформация данных

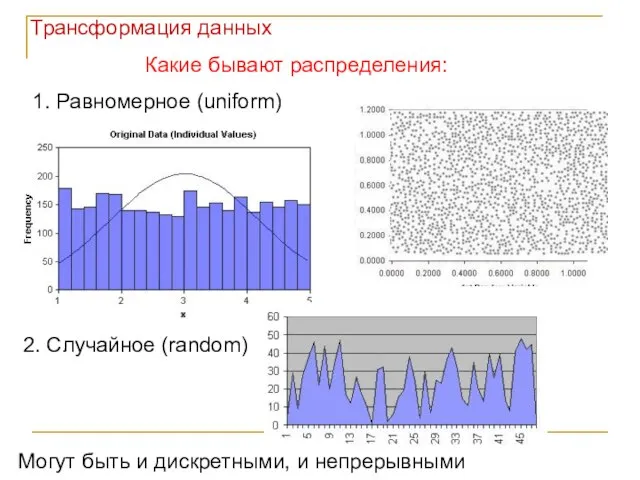
Какие бывают распределения:
1. Равномерное (uniform)
2. Случайное (random)
Могут быть и дискретными, и непрерывными
Трансформация данных

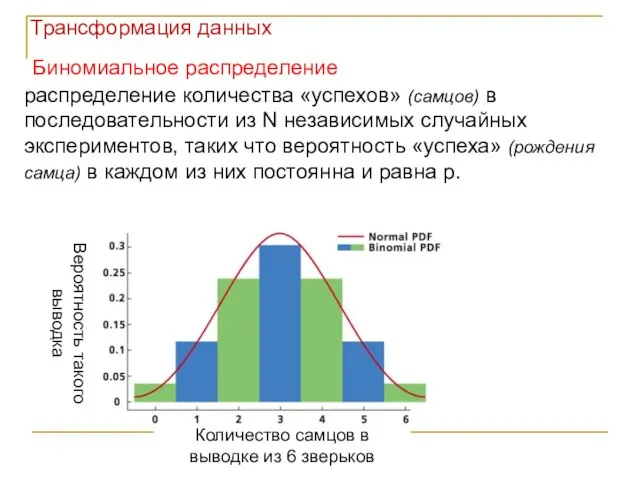
Пример: рассмотрим выводки из 6 детёнышей каждый.
Возможное соотношение самцов и самок в выводке:
6:0; 5:1; 4:2; 3:3; 2:4; 1:5; 0:6
3. Биномиальное распределение (дискретное).
Трансформация данных

Биномиальное распределение
Количество самцов в выводке из 6 зверьков
Вероятность такого выводка
распределение количества «успехов» (самцов) в последовательности из N независимых случайных экспериментов, таких что вероятность «успеха» (рождения самца) в каждом из них постоянна и равна p.
Трансформация данных

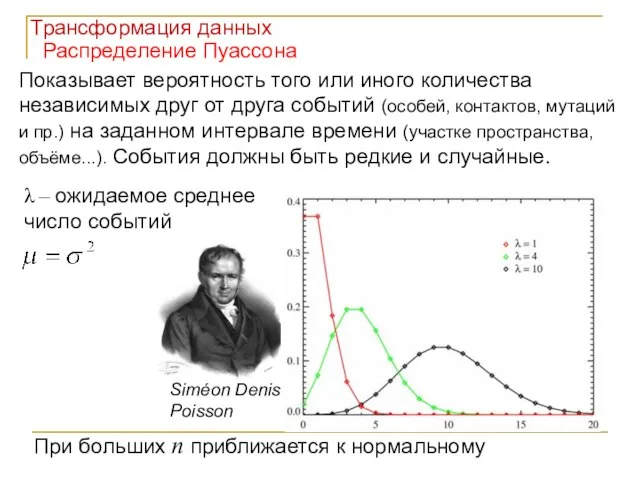
Распределение Пуассона
Показывает вероятность того или иного количества независимых друг от друга событий (особей, контактов, мутаций и пр.) на заданном интервале времени (участке пространства, объёме...). События должны быть редкие и случайные.
При больших n приближается к нормальному
Трансформация данных
λ – ожидаемое среднее число событий
Siméon Denis Poisson

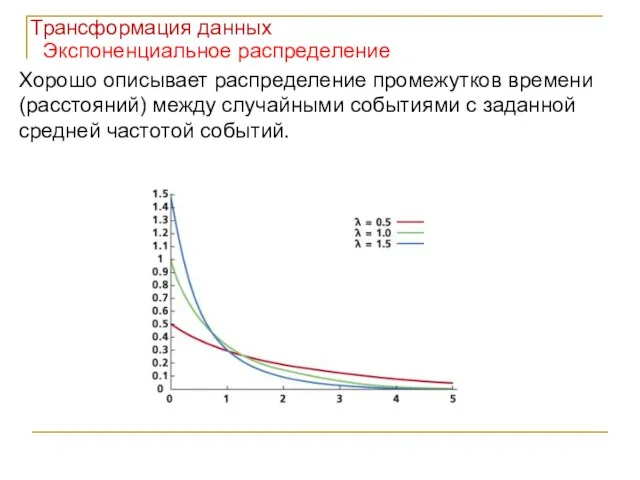
Экспоненциальное распределение
Хорошо описывает распределение промежутков времени (расстояний) между случайными событиями с заданной средней частотой событий.
Трансформация данных

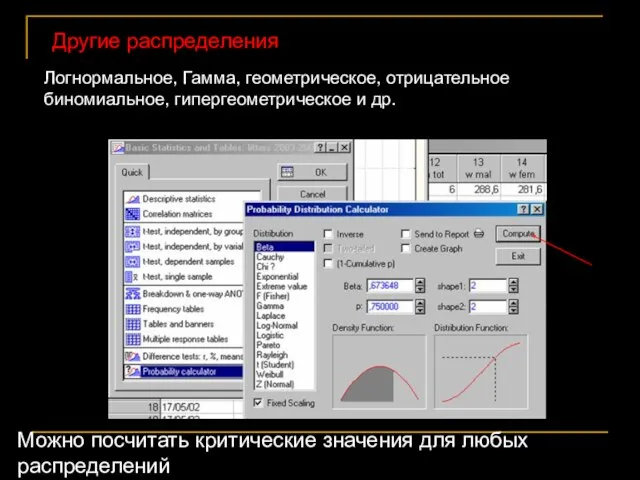
Другие распределения
Логнормальное, Гамма, геометрическое, отрицательное биномиальное, гипергеометрическое и др.
Можно посчитать критические значения для любых распределений

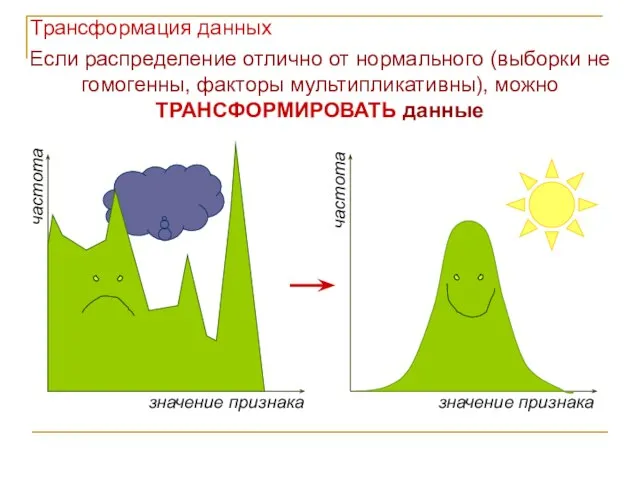
Если распределение отлично от нормального (выборки не гомогенны, факторы мультипликативны), можно
ТРАНСФОРМИРОВАТЬ данные
частота
частота
значение признака
значение признака
Трансформация данных

Логарифмическая трансформация (logarithmic transformation):
Делает симметричным скошенное вправо (positively skewed) распределение.
Используется в случае, когда чем больше среднее в группе, тем больше стандартное отклонение.
Если в результате логарифмирования получилось нормальное распределение, исходное распределение было логнормальным.
Трансформация данных

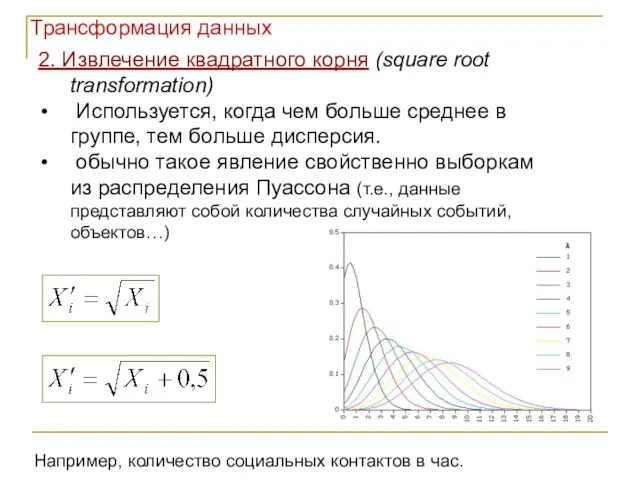
2. Извлечение квадратного корня (square root transformation)
Используется, когда чем больше среднее в группе, тем больше дисперсия.
обычно такое явление свойственно выборкам из распределения Пуассона (т.е., данные представляют собой количества случайных событий, объектов…)
Например, количество социальных контактов в час.
Трансформация данных

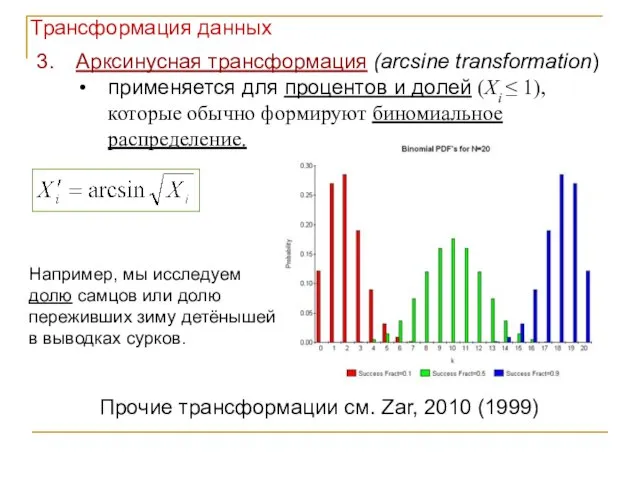
Арксинусная трансформация (arcsine transformation)
применяется для процентов и долей (Xi ≤ 1), которые обычно формируют биномиальное распределение.
Например, мы исследуем долю самцов или долю переживших зиму детёнышей в выводках сурков.
Прочие трансформации см. Zar, 2010 (1999)
Трансформация данных

Принципиально не годятся параметрические методы, если данные РАНГОВЫЕ:
мы не знаем, насколько одно значение отличается от другого.
Тут не спасёт никакая трансформация.
Непараметрические методы

Если наше распределение не удовлетворяет условиям параметрических тестов и ни одна трансформация не помогает, наш выбор -
Непараметрические методы (nonparametric methods)
Свойства распределения неизвестны, и параметры распределения (среднее, дисперсию и т. п.) мы использовать не можем
Основной подход – ранжирование (ranking) наблюдений (выстраиваем их по порядку от самого маленького значения к наибольшему).
подразумевается, что сравниваемые распределения имеют одинаковую форму и дисперсию.
= “distribution-free” tests

Мы исследуем два редких вида сумчатых. Нам важно узнать, различаются ли виды по тому, какую освещённость местообитаний они предпочитают.
Освещённость мы оценивали на глаз по 100-бальной шкале.
Фактор – вид. Группы: 1. длинноухие; 2. пятнистые
длинноухий
пятнистый
Непараметрические методы

Сравнение 2-х независимых групп:
Манн-Уитни тест (Mann-Whitney U-test)
Н0: распределение в популяции, из которой мы получили выборку длинноухих, такое же, как и в популяции, из которой выборка пятнистых.
Н1: распределения не одинаковые.
Мы ничего не говорим про параметры распределений!
Непараметрические методы
Тест Манна-Уитни можно использовать и для ранговых, и для непрерывных переменных.

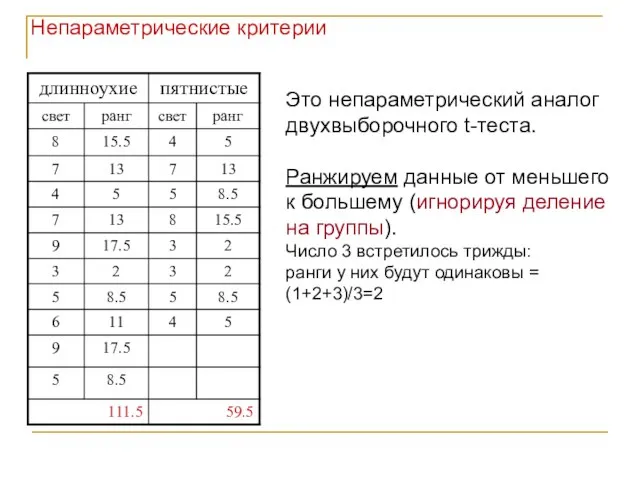
Непараметрические критерии
Это непараметрический аналог двухвыборочного t-теста.
Ранжируем данные от меньшего к большему (игнорируя деление на группы).
Число 3 встретилось трижды:
ранги у них будут одинаковы = (1+2+3)/3=2

Статистика критерия:
n1 и n2 – размер выборок,
R1 и R2 – суммы рангов в выборках.
Статистикой критерия Uobs будет меньшее из этих двух значений. Причём Н0 мы отвергнем в случае, если оно будет МЕНЬШЕ критического значения Ucv. (т.е., это исключение среди прочих критериев).
Непараметрические методы

Непараметрические критерии
Если размеры выборок больше 20, распределение статистики U приближается к нормальному со средним
Поэтому считается значение
И сравнивается с критическим значением для нормального распределения Z (наблюдаемое z должно быть по модулю больше критического).
Поэтому для маленьких выборок в статье можно приводить только U, а для больших выборок нужно приводить и U, и z.
Тест может быть односторонним и двусторонним

Сравнение 2-х независимых групп:
Тест Колмогорова-Смирнова (Kolmogorov-Smirnov two-sample test)
Отличается от теста Манн-Уитни тем, что М-У более чувствителен к различиям средних значений, медианы и т.п., а К-С тест более чувствителен к различиям распределений по форме.
Непараметрические критерии
Манн-Уитни тест более мощный.

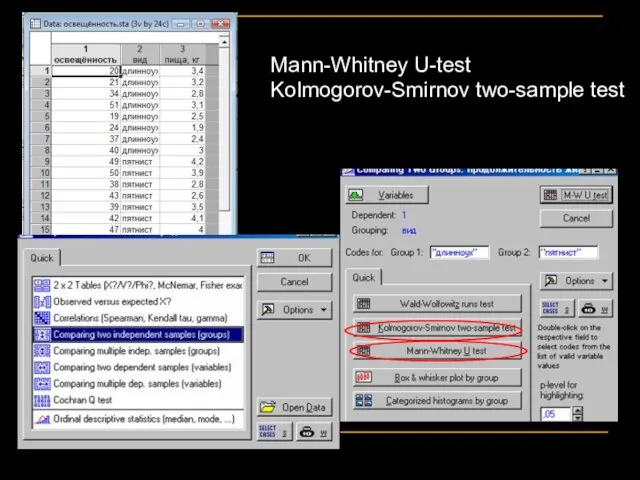
Mann-Whitney U-test
Kolmogorov-Smirnov two-sample test

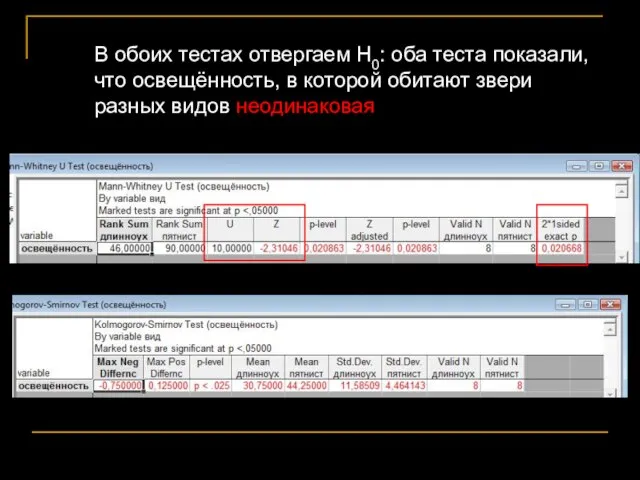
В обоих тестах отвергаем Н0: оба теста показали, что освещённость, в которой обитают звери разных видов неодинаковая

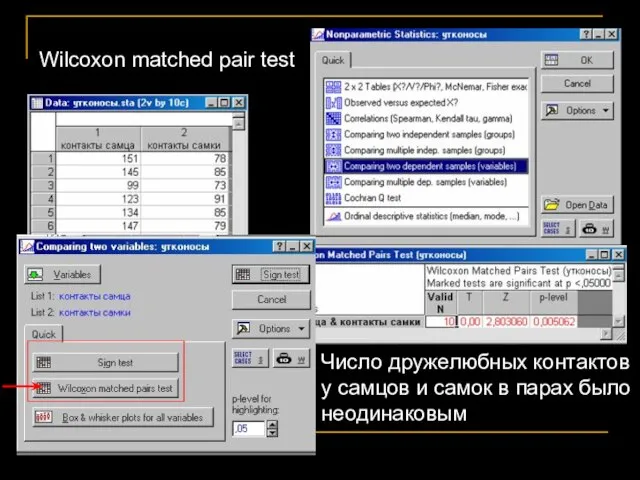
Сравнение 2-х связанных групп
Критерий Вилкоксона (Wilcoxon matched pair test)
Изучаем утконосов, и хотим знать – различается ли отношение самки к самцу и самца к самке в парах
Мы считаем частоту дружелюбных контактов со стороны самки к самцу и наоборот. У каждого самца есть по жене, а у каждой самки – по мужу!
Непараметрические методы

Фактор – пол. (1. самцы; 2. самки)
Непараметрические методы
Н0: распределение контактов в популяции, из которой мы получили выборку самцов, такое же, как и в популяции, из которой выборка самок.
Н1: распределения не одинаковые.

Считают разности между значениями в парах;
исключают нулевые разности;
присуждают абсолютным значениям (по модулю) разностей ранги;
суммируют отдельно ранги положительных и отрицательных разностей;
Наименьшая из этих сумм - статистика Т.
Отвергаем Н0, если Т меньше Tcv.
Непараметрические методы
Аналог t-теста для двух связанных выборок. При числе пар >100 Т апроксимируется нормальным распределением.
Предполагается, что распределение этих разностей симметрично относительно медианы

Wilcoxon matched pair test
Число дружелюбных контактов у самцов и самок в парах было неодинаковым

Непараметрические критерии
Сравнение 2-х связанных групп
Знаковый тест (Sign test)
Считают разности в парах, но не ранжируют их, а просто определяют число положительных и отрицательных разностей (нули исключают). Сравнивают их соотношение с 1:1. (биномиальным тестом)
Подходит для случаев, когда точные значения переменной не известны.
Имеет низкую мощность, поэтому применяется только в больших выборках (больше 20 пар).

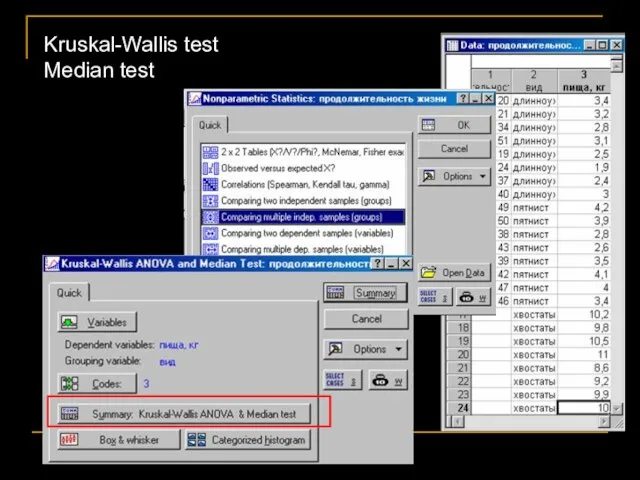
Непараметрические критерии
Сравнение ≥3-х независимых групп
Тест Крускала-Уоллиса (Kruskal-Wallis test)
Мы получили возможность включить в работу третий, особенно редкий вид сумчатого. Теперь нас интересует, различается ли доля растительной пищи, которую съедают за день особи этих видов.
Фактор – вид. Группы: 1. длинноухие; 2. пятнистые; 3. хвостатые

Непараметрические критерии
Критерий Крускал-Уоллиса (Kruskal-Wallis test)
Непараметрический аналог One-way ANOVA
на 95% настолько же мощный, как и ANOVA;
для 2-х групп идентичен Манн-Уитни тесту;
подразумевает сходство форм и дисперсий в распределениях (хотя бы на глаз)

все значения ранжируются от меньшего к большему (игнорируя деление на группы);
Считается сумма рангов в каждой группе;
считается статистика H(df, N).
сумма рангов в каждой группе
размер группы
общий размер выборки
Н0: распределение в популяциях, из которых мы получили выборки, одинаковое.
Н1: распределения не одинаковые.
Непараметрические критерии

Непараметрические критерии
При маленьких выборок и 3-5-и групп считается Н-статистика.
Для больших выборок (или >5-и групп) Н апроксимируется распределением χ2.
Критерий Крускал-Уоллиса (Kruskal-Wallis test)

Непараметрические критерии
Сравнение ≥2-х независимых групп
Медианный тест (Median test)
Считается общая медиана для всех групп (получается, что это не непараметрический тест, а distribution-free).
Затем критерием χ2 (см. Частотные критерии) сравнивают числа значений, которые больше и которые меньше общей медианы в каждой из групп (табличка 2 х k).
Подходит для выборок, в которых часть наблюдений выходит за пределы шкалы (или их точные значения неизвестны).
Но имеет очень низкую мощность – лишь 67% мощности Манн-Уитни теста или теста Крускалла-Уоллеса.

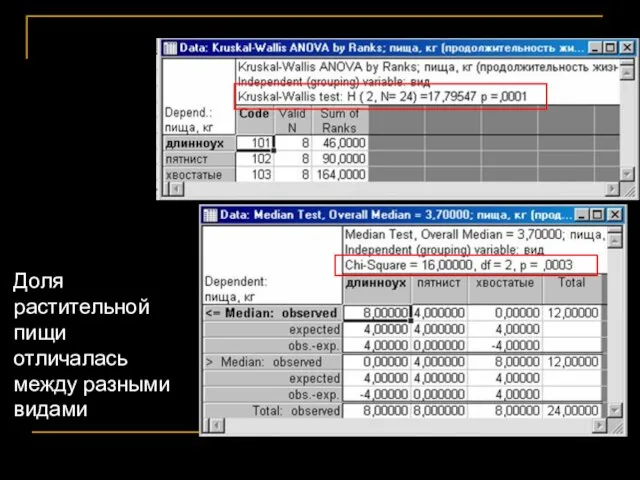
Kruskal-Wallis test
Median test

Доля растительной пищи отличалась между разными видами

Непараметрические критерии
Критерий Крускал-Уоллиса (Kruskal-Wallis test)
Хотелось бы провести после сравнения нескольких групп пост-хок тест (апостериорное сравнение), по аналогии с тестом Тьюки.
Такие тесты существуют – Nemenyi test, Dunn’s test (Zar, 1999 или 2010).
Только в Statistica их нет, поэтому можно их считать вручную, либо задавать формулу в Statistica и какой-л. другой программе

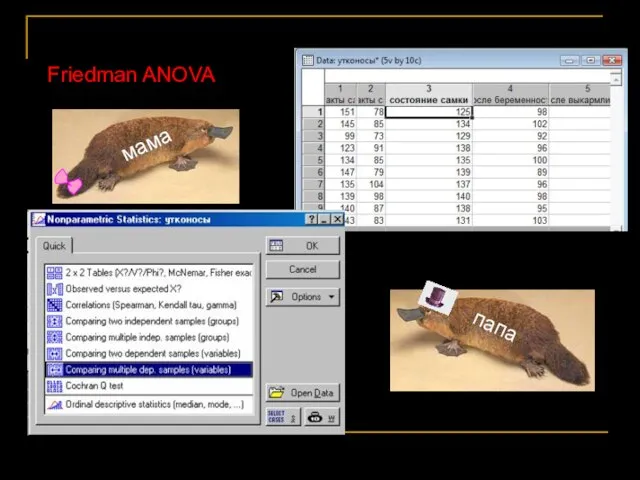
Непараметрические критерии
Сравнение ≥3 связанных групп
Критерий Фридмана (Friedman ANOVA)
У утконосов родились детёныши, и мы хотим знать, изменялось ли физическое состояние самок после беременности и после выкармливания потомства (мы оценивали его в баллах по упитанности и состоянию шерсти).
состояние до беременности;
после рождения детей;
после выкармливания детёнышей

Непараметрические критерии
Критерий Фридмана (Friedman ANOVA)
для двух групп эквивалентен Знаковому тесту (sign test);
по сравнению с аналогичными параметрическими тестами, для 2-х групп имеет всего 64% мощности, для 3-х – 72%, для 100 стремится к 95%.
Основан на том, что значения ранжируются меньшего к большему внутри каждой строки. Потом суммируют ранги для каждого столбца и считают статистику χ2r, которая имеет распределение χ2.
Нулевая и альтернативная гипотезы - по аналогии с предыдущими тестами, о сходстве выборок.

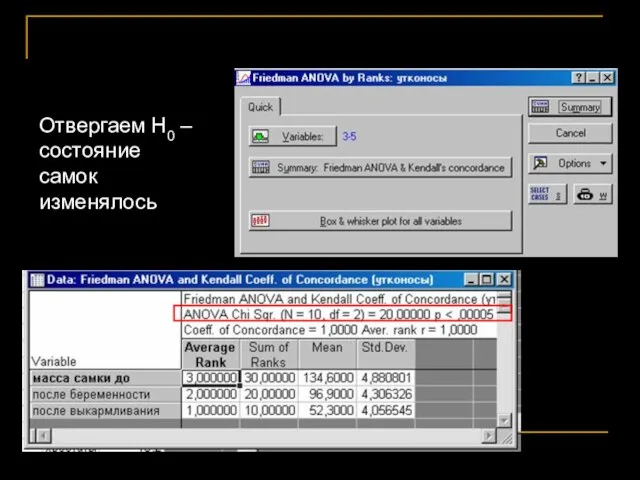
Friedman ANOVA

Отвергаем Н0 – состояние самок изменялось

Итак, при выборе теста важно, что:
Параметрические тесты более мощные, чем непараметрические;
Непараметрические безопаснее в плане ошибки 1-го рода;
Чем больше размер выборки, тем менее критичны требования к распределению (по Центральной предельной теореме); для выборок N ≥ 100 используют параметрические тесты даже при больших отклонениях от нормального распределения.
АНОВА не очень чувствительна к отклонениям от нормального распределения (для одинаковых по размеру групп).

У нас есть выборка. Данные – качественные.
Вопрос: соответствует ли распределение в популяции, из которой получена выборка, теоретическому распределению? (которое мы сами определяем).
Ответ дадут КРИТЕРИИ СОГЛАСИЯ (Tests for goodness of fit).
Частотные критерии
Придумал χ2 статистику ещё в 1900 году!
Пример с игральной костью: как проверить, не кривая ли она? Очевидно, что бросая её 120 раз маловероятно получить ровно по 20 бросков на каждую сторону. Насколько же допустимы различия?

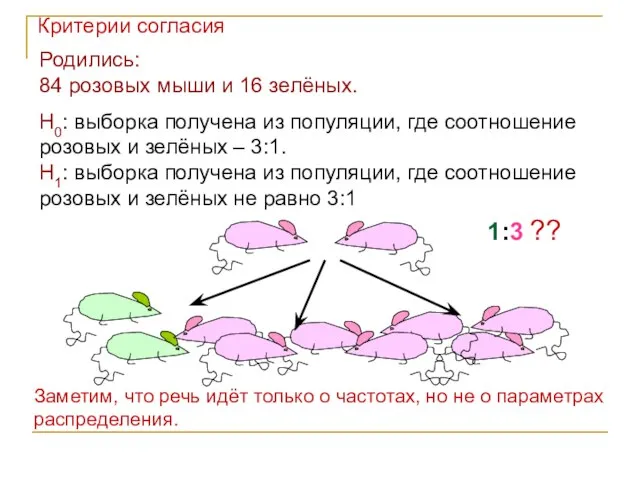
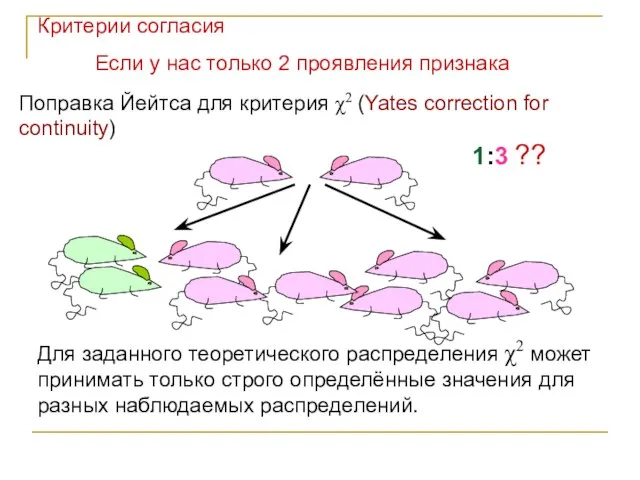
1:3 ??
Родились:
84 розовых мыши и 16 зелёных.
H0: выборка получена из популяции, где соотношение розовых и зелёных – 3:1.
H1: выборка получена из популяции, где соотношение розовых и зелёных не равно 3:1
Критерии согласия
Заметим, что речь идёт только о частотах, но не о параметрах распределения.

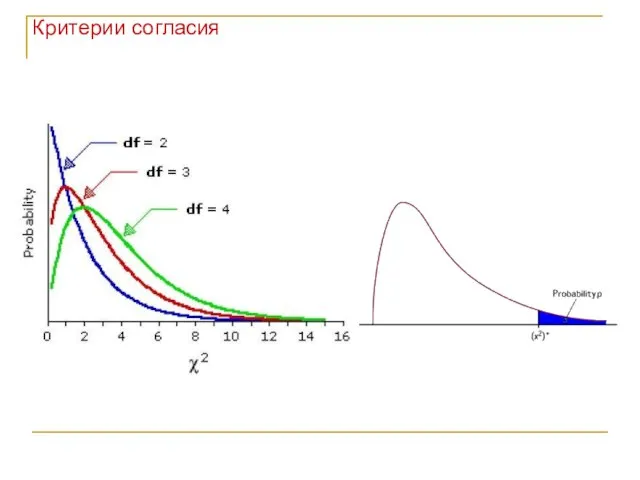
χ2cv = 3.841<4.320
H0 отвергаем – соотношение мышей не соответствует ожидаемому
Чем больше значение χ2,тем хуже наши данные соответствуют теоретическому распределению – тем меньше р
p=0.038
df = k-1=1
Критерии согласия

Критерии согласия

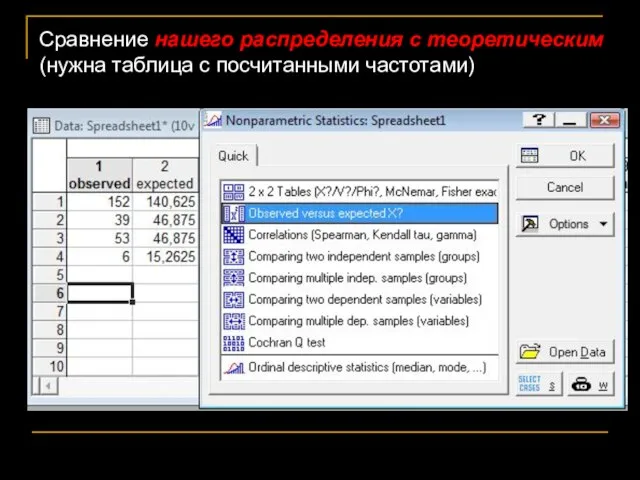
Категорий может быть сколько угодно.
Родились:
152 розовых мыши с острым хвостом; 39 розовых с курчавым хвостом; 53 зелёных с острым, 6 зелёных с курчавым.
H0: выборка получена из популяции, где соотношение фенотипов – 9:3:3:1.
H1: выборка получена из популяции, где соотношение фенотипов не равно 9:3:3:1
Критерии согласия

+
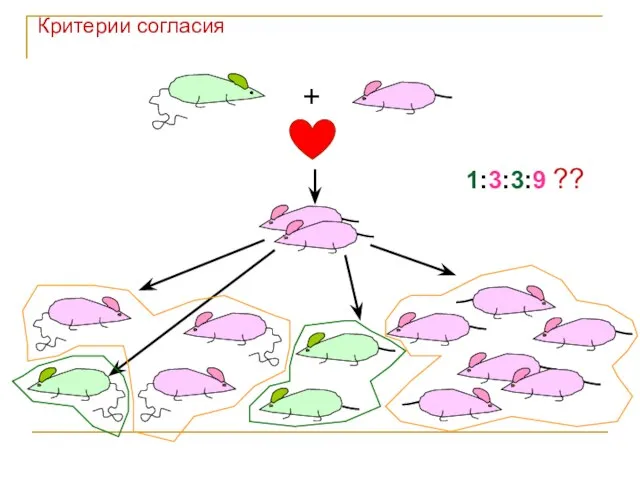
1:3:3:9 ??
Критерии согласия

Важное замечание:
В всех критериях согласия H0 гипотеза – о том, что форма распределений ОДИНАКОВА.
То есть, когда мы ищем подтверждение тому, что наши данные удовлетворяют некоторому распределению, мы должны радоваться, получив p>>0.05!
Критерии согласия

Zar, 1999:
Если мы сравнили распределение с теоретическим, получили отличия (!), а теперь хотим показать, из-за какой именно категории эти отличия возникли, можно отдельно сравнить с теоретическим распределением остальные категории, а затем – отношение этой категории к остальным.
Т.е., если нам кажется, что всё портят зелёные мыши с курчавыми хвостами, сравним:
1. соотношение остальных мышей с 9:3:3;
2. отношение зелёных-курчавых к остальным с 1:15.
Критерии согласия

у нас одна выборка
Переменная качественная
мы сравниваем наблюдаемые частоты с ожидаемыми (observed and expected)
Критерий χ2 Пирсона (Pearson Chi-square test)
Итак:
Критерии согласия

Сравнение нашего распределения с теоретическим (нужна таблица с посчитанными частотами)

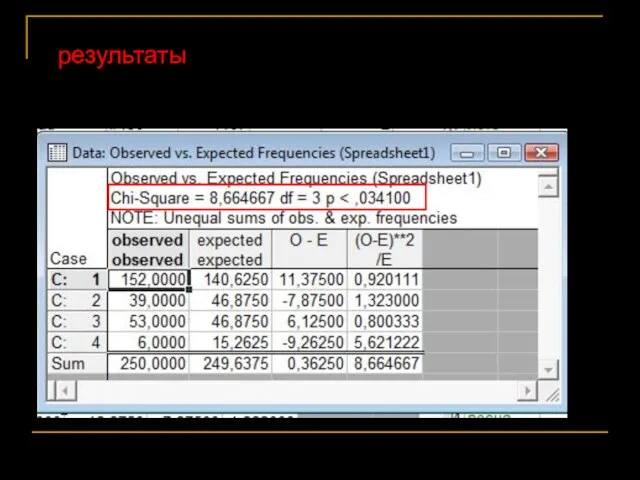
результаты

Поправка Йейтса для критерия χ2 (Yates correction for continuity)
1:3 ??
Если у нас только 2 проявления признака
Для заданного теоретического распределения χ2 может принимать только строго определённые значения для разных наблюдаемых распределений.
Критерии согласия

Например: если ожидаемые частоты – 75 и 25, то значения χ2 будут
для 84 и 16 – 4.32,
для 83 и 17 – 3.14,
для 82 и 18 – 2.61
промежуточных значений не может быть для данных ожидаемых частот
Но χ2 распределение непрерывное. И для заданного уровня значимости p мы не найдём точно соответствующего ему значения χ2.
χ2 с поправкой Йейтса:
(для больших N не нужен)
Делает тест более консервативным.
Критерии согласия

Биномиальный тест
Элементарный тест для сравнения двух частот с теоретическими (для маленьких выборок, легко считать вручную). Большие выборки – задача для теста χ2.
Пример с котом Гусом: у нас есть подозрение, что он правша. Мы дали ему игрушку на резинке, он ударил по ней 10 раз: 8 - правой, 2 – левой. Справедливо ли наше подозрение?
Пример с Т-образным лабиринтом: 10 мышей пошли налево, 3 – направо.
Источники:
Zar, 2010 (1999).
http://udel.edu/~mcdonald/statexactbin.htm

Замечательный тест Колмогорова-Смирнова для ранговых данных (Kolmogorov-Smirnov goodness of fit for discrete ordinal scale data).
35 кошек выбирают из 5 типов корма, различающихся по влажности. Случаен ли выбор или есть предпочтения?
То есть, 5 типов корма можно проранжировать от самого влажного к самому сухому, это не просто качественные признаки. Мощность такого теста выше, чем χ2 , но его нет в Staristica.
Zar, 2010 (1999).
Критерии согласия

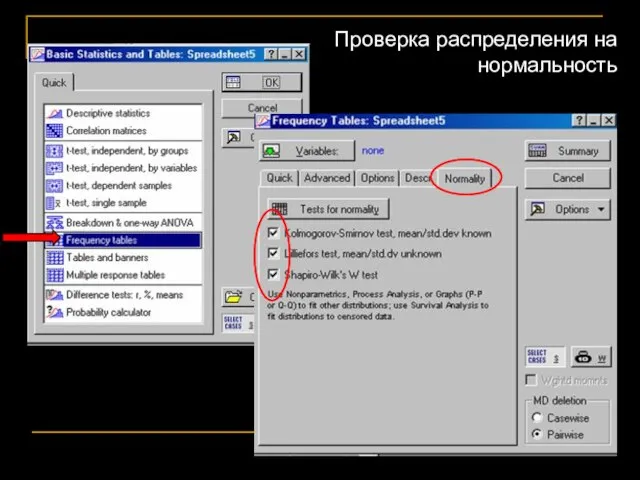
Соответствует ли распределение мотыльков на дереве НОРМАЛЬНОМУ РАСПРЕДЕЛЕНИЮ?
Переменная – высота от земли в метрах
Тест Колмогорова-Смирнова (Kolmogorov-Smirnov test) (если известны дисперсия и среднее в популяции) D-статистика.
Lilliefors test – если НЕизвестны дисперсия и среднее в популяции – «улучшенный К-С тест»
Shapiro-Wilk’s W test (самый мощный, размер выборки до 5000) – наиболее предпочтительный.
Тесты на соответствие непрерывным распределениям
Критерии согласия

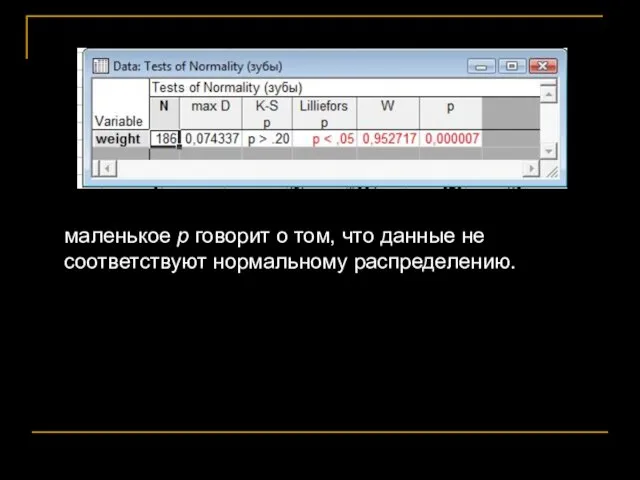
Проверка распределения на нормальность

маленькое p говорит о том, что данные не соответствуют нормальному распределению.

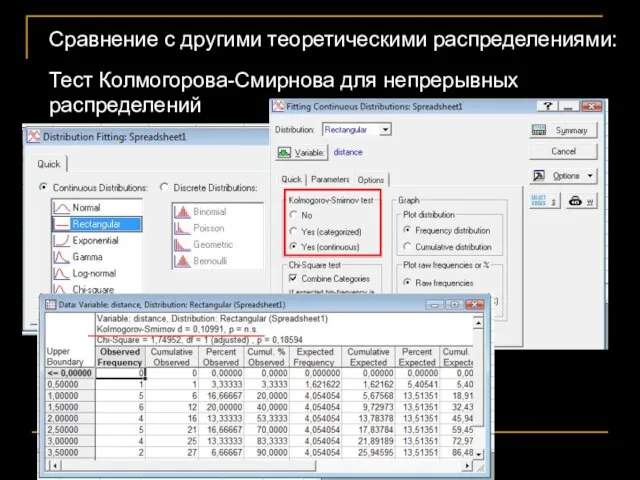
Сравнение с другими теоретическими распределениями:
Тест Колмогорова-Смирнова для непрерывных распределений

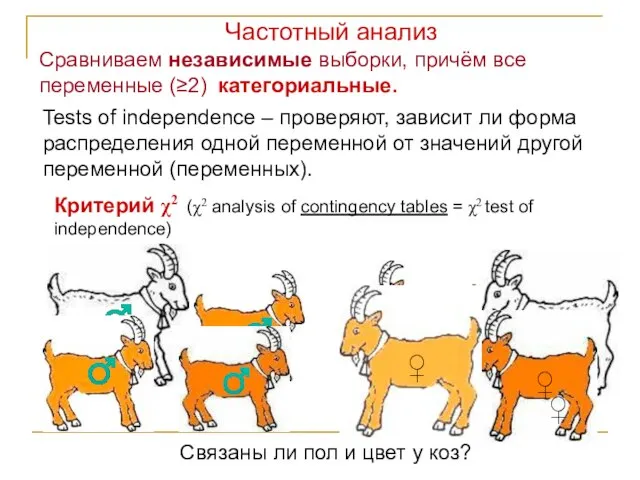
Сравниваем независимые выборки, причём все переменные (≥2) категориальные.
♂
Связаны ли пол и цвет у коз?
♂
♀
Частотный анализ
Критерий χ2 (χ2 analysis of contingency tables = χ2 test of independence)
Tests of independence – проверяют, зависит ли форма распределения одной переменной от значений другой переменной (переменных).

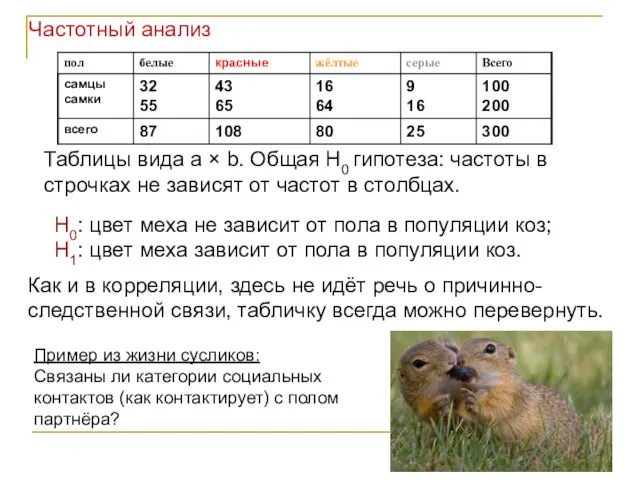
H0: цвет меха не зависит от пола в популяции коз;
H1: цвет меха зависит от пола в популяции коз.
Пример из жизни сусликов:
Связаны ли категории социальных контактов (как контактирует) с полом партнёра?
Таблицы вида a × b. Общая Н0 гипотеза: частоты в строчках не зависят от частот в столбцах.
Как и в корреляции, здесь не идёт речь о причинно-следственной связи, табличку всегда можно перевернуть.
Частотный анализ

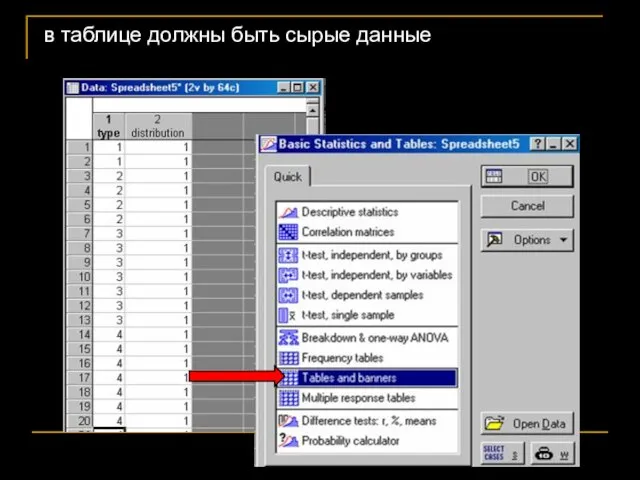
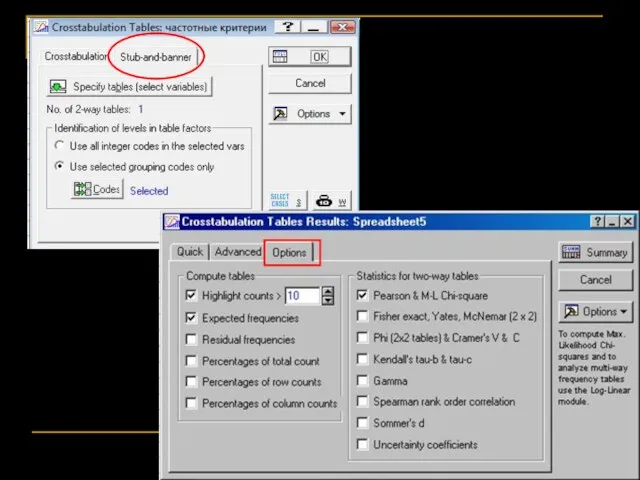
Частотный анализ
Мы для каждой ячейки рассчитываем ожидаемую частоту (на основе общих частот для столбцов и строк).
Потом считаем обыкновенную статистику χ2 :

в таблице должны быть сырые данные

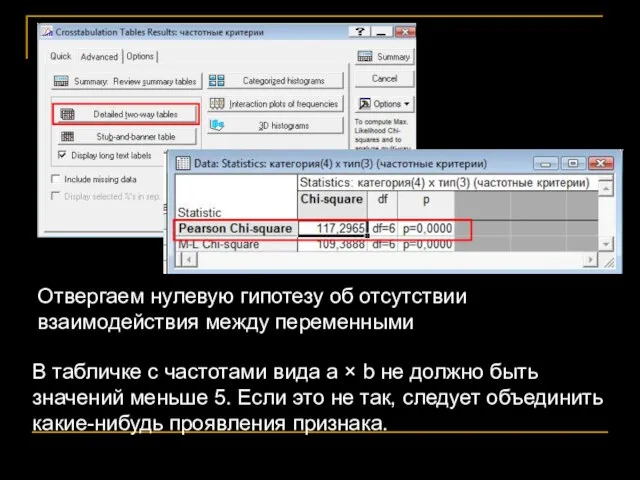
В табличке с частотами вида a × b не должно быть значений меньше 5. Если это не так, следует объединить какие-нибудь проявления признака.
Отвергаем нулевую гипотезу об отсутствии взаимодействия между переменными

Zar, 1999:
Если вы не отвергли связь переменных (!), а теперь хотите показать, из-за какой именно категории есть связь, можно отдельно проверить связь переменных на остальных категориях, а затем – отношение этой категории к остальным.
Например, если самцы и самки коз отличаются, по-видимому, только по соотношению белых коз, можно:
исключить белых, проверить связь пола и цвета для остальных;
проверить связь пола и присутствия белого цвета у козы.
Частотный анализ

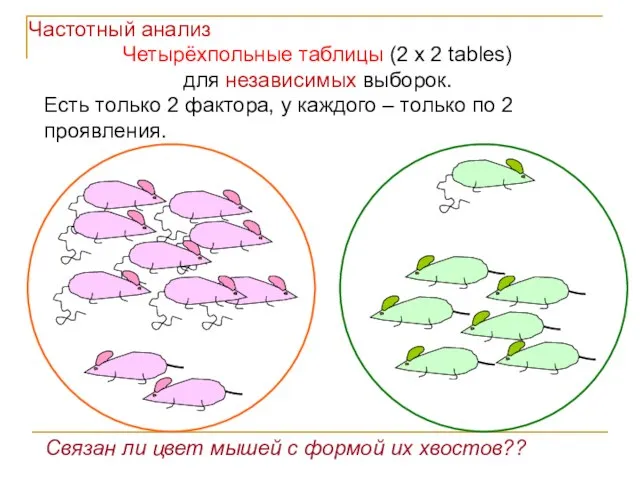
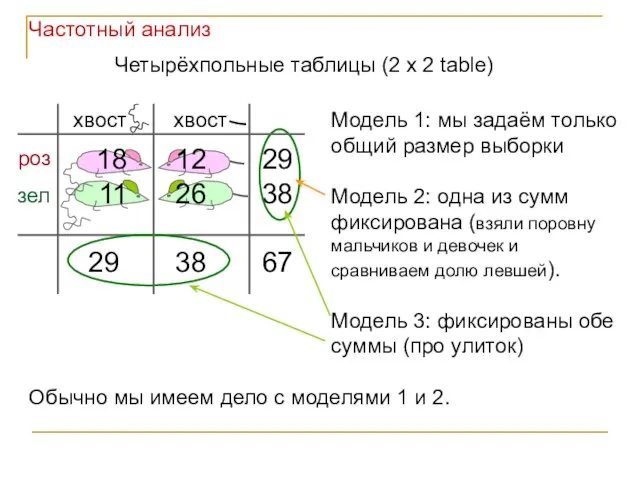
Четырёхпольные таблицы (2 x 2 tables) для независимых выборок.
Есть только 2 фактора, у каждого – только по 2 проявления.
Связан ли цвет мышей с формой их хвостов??
Частотный анализ

18 12 29
11 26 38
29 38 67
Четырёхпольные таблицы (2 x 2 table)
Модель 1: мы задаём только общий размер выборки
Модель 2: одна из сумм фиксирована (взяли поровну мальчиков и девочек и сравниваем долю левшей).
Модель 3: фиксированы обе суммы (про улиток)
хвост
хвост
роз
зел
Обычно мы имеем дело с моделями 1 и 2.
Частотный анализ

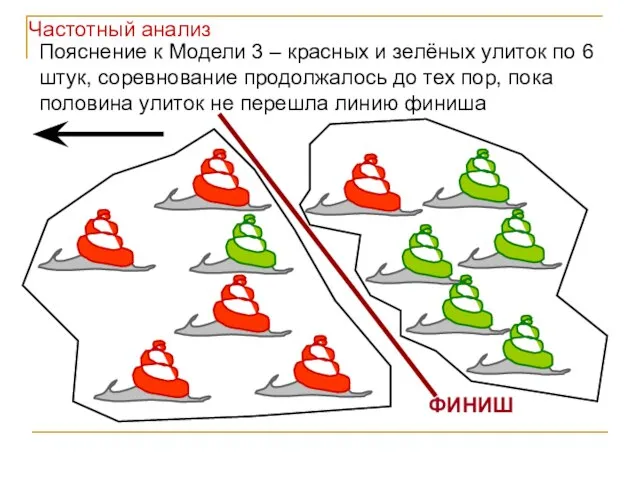
ФИНИШ
Пояснение к Модели 3 – красных и зелёных улиток по 6 штук, соревнование продолжалось до тех пор, пока половина улиток не перешла линию финиша
Частотный анализ

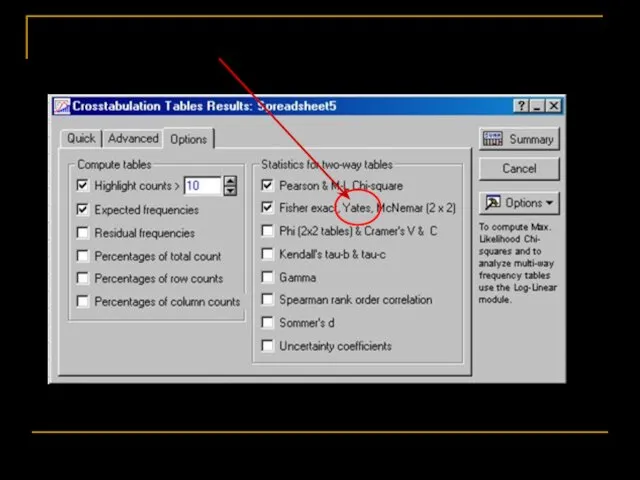
Критерий χ2 (Chi-square) с поправкой Йейтса.
Если в табличке сырые данные, а не готовая четырёхпольная таблица – Tables and Banners.
Если готовая таблица – 2 x 2 tables.
Принцип введения поправки – тот же, что для сравнения наблюдаемых и ожидаемых частот, делает тест более консервативным.
Не нужна для больших выборок. В Statistica: поправку вводят, если хотя бы одна частота меньше 10.
Лучше всего подходит для модели 1.
Частотный анализ

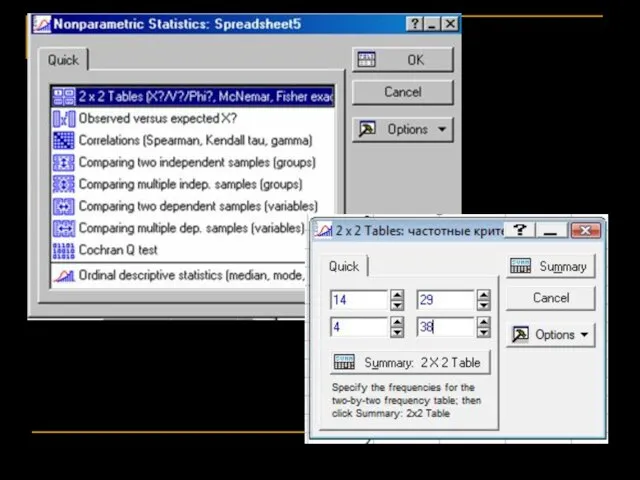
Точный критерий Фишера (Fisher exact test)
Годится, если одна из частот меньше 5 и вообще, для небольших выборок. Подходит для 3-й модели. Вообще, лучший из 2х2 тестов (Zar, 1999)
Н0: район, где живёт скунс, и заболеваемость не связаны друг с другом;
Н1 : между районом и заболеванием есть связь.
Частотный анализ

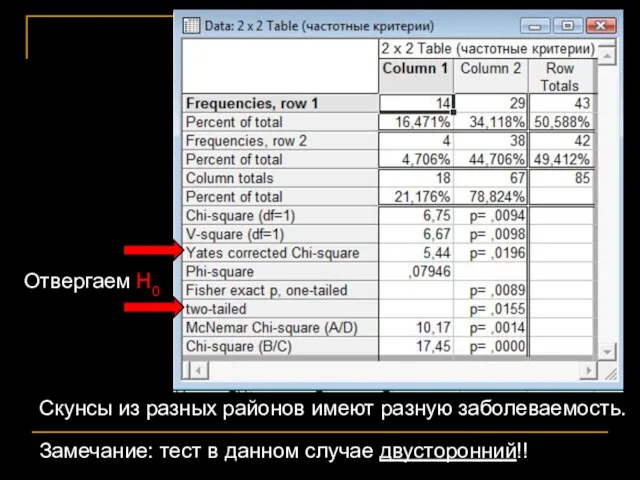
Скунсы из разных районов имеют разную заболеваемость.
Замечание: тест в данном случае двусторонний!!
Отвергаем Н0

Односторонний тест Фишера:
Для случаев, когда мы заранее знаем, куда может отклониться соотношение частот.
Например, мы даём лекарство больным зверям и сравниваем, сколько из них выздоровело по сравнению с контрольной группой.
Предполагается, что лекарство не может ухудшить состояние зверей, а только может либо вылечить, либо нет.
Частотный анализ

Phi-square – показатель корреляции между качественными переменными.
V-square – разновидность χ2 теста.
Все эти тесты подразумевали, что выборки независимы (например, каждая особь входит только в одну из ячеек).
Частотный анализ

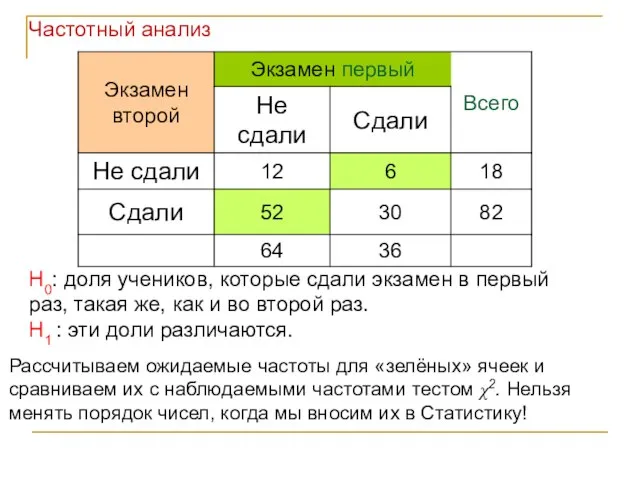
Критерий Мак-Немара (McNemar Chi-square)
Анализ 2-х связанных выборок:
Требуется специальная организация таблицы
Мы провели в сентябре экзамен по математике. Из 100 учеников 36 сдали экзамен, остальные - провалили. Потом мы подвергли всех учеников интенсивным занятиям по математике.
Для тех же учеников мы провели экзамен во 2-й четверти.
Повлияли ли занятия на успеваемость?
Частотный анализ
По сути дела, это просто двухвыборочный тест для связанных выборок – аналог критерия Вилкоксона, только для качественных переменных

Рассчитываем ожидаемые частоты для «зелёных» ячеек и сравниваем их с наблюдаемыми частотами тестом χ2. Нельзя менять порядок чисел, когда мы вносим их в Статистику!
Н0: доля учеников, которые сдали экзамен в первый раз, такая же, как и во второй раз.
Н1 : эти доли различаются.
Частотный анализ

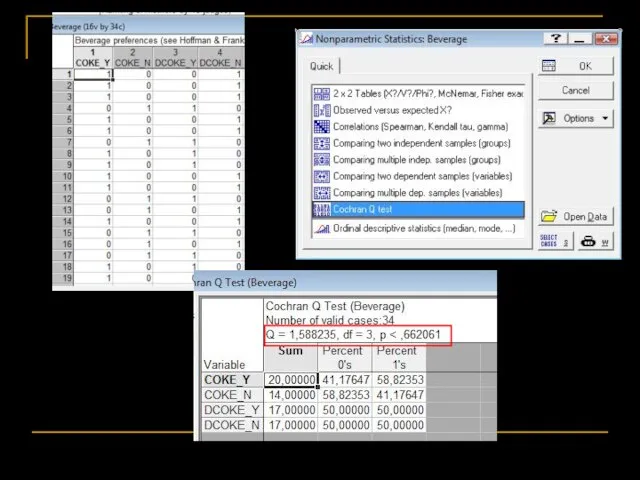
Частотный анализ
Анализ ≥3-х связанных выборок:
Cochran’s Q test
Сравнивает несколько связанных измерений одной БИНАРНОЙ переменной.
(например, присутствие/отсутствие гельминтов у самок суслика сразу после спячки – во время беременности – во время лактации – перед спячкой).

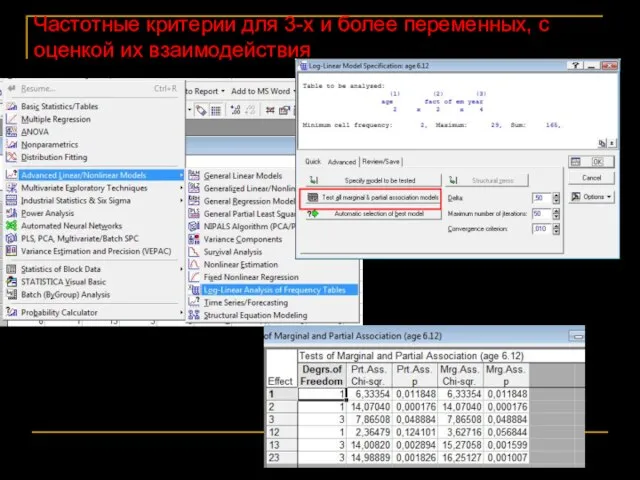
Частотные критерии для 3-х и более переменных, с оценкой их взаимодействия

Задания.
Хазел Нат продаёт смесь орехов. На упаковке написано, что в пачке содержится 30% кешью, 20% бразильских орехов, 20% грецких, 30% лесных. Мы хотим проверить, так ли это, взяли большую пачку и посчитали в ней разные орехи (200 орехов). Н0? Статистический критерий?
Мы хотим прививать детям Сибири бережное отношение к природе. Мы выбрали 100 первоклашек и спросили их, можно ли охотиться на кабаргу (78 ответили «да», 22 – «нет»). Потом им показывали фильмы и рассказывали о местной фауне весь год. Весной этих же детей спросили о том же. Из тех, кто был за охоту, 18 опять ответили «да», 60 – «нет». Из тех, кто был против – 2 ответили «да», 20 - «нет». Н0? Статистический критерий?
Издатели хотят узнать, насколько наличие цветных картинок в статье помогает воспринимать текст. Выбрали 13 студентов, и каждому дали два текста одинаковой сложности - с цветными и чёрно-белыми картинками. Потом попросили оценить сложность текста по 10-бальной шкале. Влияют ли цветные картинки на восприятие текста? Н0? Статистический критерий?

4. Проходят соревнования по фигурному катанию. Мы хотим узнать, влияет ли жанр исполняемой музыкальной композиции во время выступления на оценку фигуриста. 30 фигуристам случайным образом заранее предложили композиции на основе классической музыки, тяжёлого рока и поп-музыки (по 10 композиций на жанр). Жюри выставило оценки. Зависят ли они от музыкального жанра? Н0? Статистический критерий?
5. Мы хотим знать, зависит ли вероятность принести потомство от возраста самки у белок. Мы не знаем точный возраст зверьков, можем лишь отличить взрослых от годовалых. Мы исследовали 50 годовалых и взрослых самок, и выяснили, какие самки из них принесли выводки, какие – остались холостыми. Н0? Статистический критерий?