Слайд 2
Pachshenko
Galina Nikolaevna
Associate Professor of Information System Department,
Candidate

of Technical Science
Слайд 4Topics
Types of Optimization Algorithms used in Neural Networks
Gradient descent

Слайд 5Have you ever wondered which optimization algorithm to use for your Neural

network Model to produce slightly better and faster results by updating the Model parameters such as Weights and Bias values .
Should we use Gradient Descent or Stochastic gradient Descent?
Слайд 6What are Optimization Algorithms ?

Слайд 7Optimization algorithms helps us to minimize (or maximize) an Objective function (another name for Error function) E(x) which is

simply a mathematical function dependent on the Model’s internal learnable parameters which are used in computing the target values(Y) from the set of predictors(X) used in the model.
Слайд 8For example — we call the Weights(W) and the Bias(b) values of the neural network as its internal

learnable parameters which are used in computing the output values and are learned and updated in the direction of optimal solution i.e minimizing the Loss by the network’s training process and also play a major role in the training process of the Neural Network Model .
Слайд 9The internal parameters of a Model play a very important role in

efficiently and effectively training a Model and produce accurate results.
Слайд 10This is why we use various Optimization strategies and algorithms to update

and calculate appropriate and optimum values of such model’s parameters which influence our Model’s learning process and the output of a Model.
Слайд 11Optimization Algorithm falls in 2 major categories

Слайд 12First Order Optimization Algorithms — These algorithms minimize or maximize a Loss function E(x) using its Gradient values

with respect to the parameters. Most widely used First order optimization algorithm is Gradient Descent.
Слайд 13The First order derivative tells us whether the function is decreasing or

increasing at a particular point. First order Derivative basically give us a line which is Tangential to a point on its Error Surface.
Слайд 14What is a Gradient of a function?

Слайд 15A Gradient is simply a vector which is a multi-variable generalization of a derivative(dy/dx) which

is the instantaneous rate of change of y with respect to x.
Слайд 16The difference is that to calculate a derivative of a function which

is dependent on more than one variable or multiple variables, a Gradient takes its place. And a gradient is calculated using Partial Derivatives . Also another major difference between the Gradient and a derivative is that a Gradient of a function produces a Vector Field.
Слайд 17A Gradient is represented by a Jacobian Matrix — which is simply a Matrix consisting of first order partial

Derivatives(Gradients).
Слайд 18Hence summing up, a derivative is simply defined for a function dependent

on single variables , whereas a Gradient is defined for function dependent on multiple variables.
Слайд 19Second Order Optimization Algorithms — Second-order methods use the second order derivative which is also called Hessian to

minimize or maximize the Loss function.
Слайд 20The Hessian is a Matrix of Second Order Partial Derivatives. Since the second derivative is costly

to compute, the second order is not used much .
Слайд 21The second order derivative tells us whether the first derivative is increasing or decreasing

which hints at the function’s curvature.
Second Order Derivative provide us with a quadratic surface which touches the curvature of the Error Surface.
Слайд 22Some Advantages of Second Order Optimization over First Order —
Although the Second Order

Derivative may be a bit costly to find and calculate, but the advantage of a Second order Optimization Technique is that is does not neglect or ignore the curvature of Surface. Secondly, in terms of Step-wise Performance they are better.
Слайд 23What are the different types of Optimization Algorithms used in Neural Networks ?

Слайд 24Gradient Descent
Variants of Gradient Descent: Batch Gradient Descent; Stochastic gradient descent; Mini Batch Gradient Descent

Слайд 25Gradient Descent is the most important technique and the foundation of how we

train and optimize Intelligent Systems. What is does is —
Слайд 26“Gradient Descent — Find the Minima , control the variance and then update the Model’s

parameters and finally lead us to Convergence.”
Слайд 27θ=θ−η⋅∇J(θ)
— is the formula of the parameter updates, where ‘η’ is the learning rate ,’∇J(θ)’ is

the Gradient of Loss function-J(θ) w.r.t parameters-‘θ’.
Слайд 28The parameter η is the training rate. This value can either set

to a fixed value or found by one-dimensional optimization along the training direction at each step. An optimal value for the training rate obtained by line minimization at each successive step is generally preferable. However, there are still many software tools that only use a fixed value for the training rate.
Слайд 29It is the most popular Optimization algorithms used in optimizing a Neural

Network. Now gradient descent is majorly used to do Weights updates in a Neural Network Model , i.e update and tune the Model’s parameters in a direction so that we can minimize the Loss function (or cost function).
Слайд 30Now we all know a Neural Network trains via a famous technique

called Backpropagation , in which we first propagate forward calculating the dot product of Inputs signals and their corresponding Weights and then apply a activation function to those sum of products, which transforms the input signal to an output signal and also is important to model complex Non-linear functions and introduces Non-linearities to the Model which enables the Model to learn almost any arbitrary functional mappings.
Слайд 31After this we propagate backwards in the Network carrying Error terms and updating Weights values using Gradient Descent, in

which we calculate the gradient of Error(E) function with respect to the Weights (W) or the parameters , and update the parameters (here Weights) in the opposite direction of the Gradient of the Loss function w.r.t to the Model’s parameters.
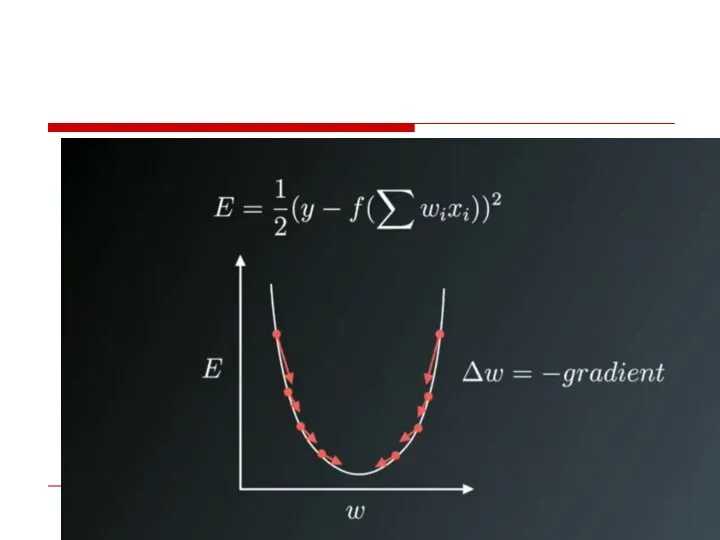
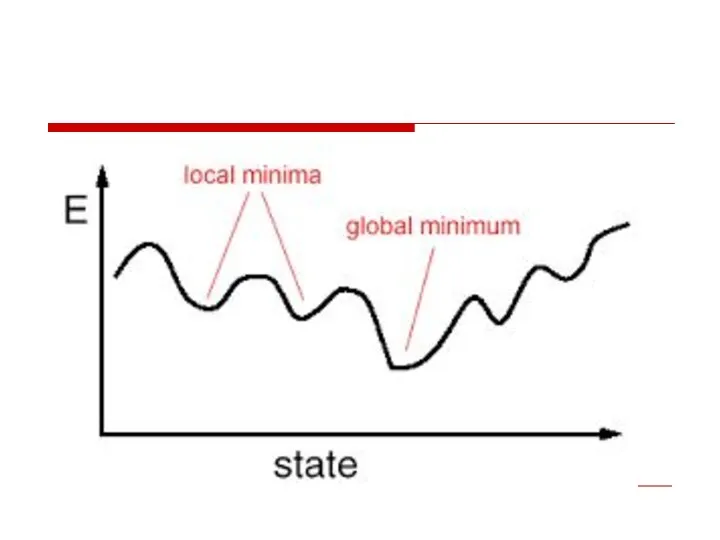
Слайд 33The image on above shows the process of Weight updates in the

opposite direction of the Gradient Vector of Error w.r.t to the Weights of the Network. The U-Shaped curve is the Gradient(slope).
Слайд 34As one can notice if the Weight(W) values are too small or too

large then we have large Errors , so want to update and optimize the weights such that it is neither too small nor too large , so we descent downwards opposite to the Gradients until we find a local minima.
Слайд 35Gradient Descent
we descent downwards opposite to the Gradients until we find a local
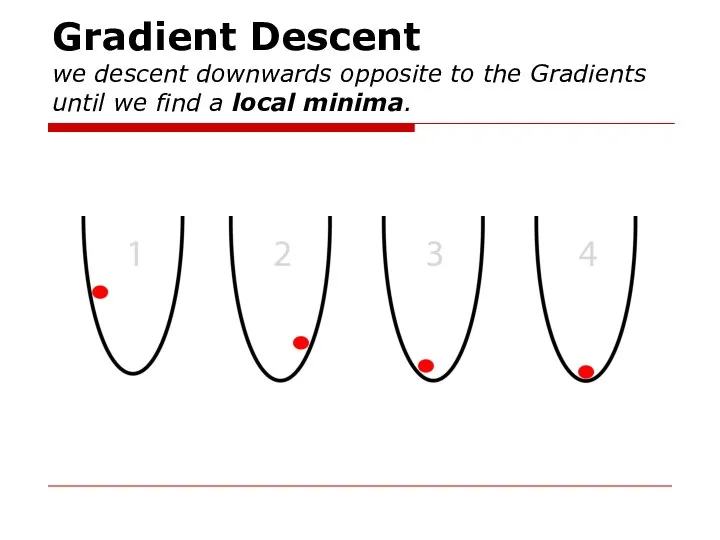
minima.
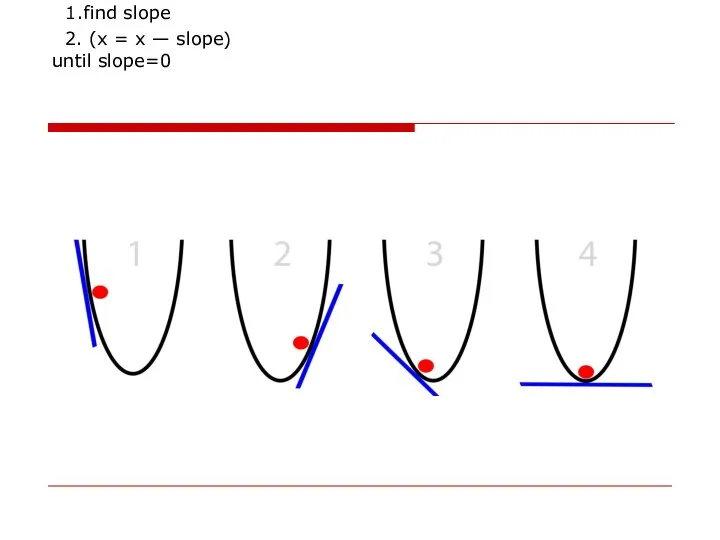
Слайд 36 1.find slope
2. (x = x — slope)
until slope=0
Слайд 381. find slope
2. alpha = 0.1 (or any number from 0
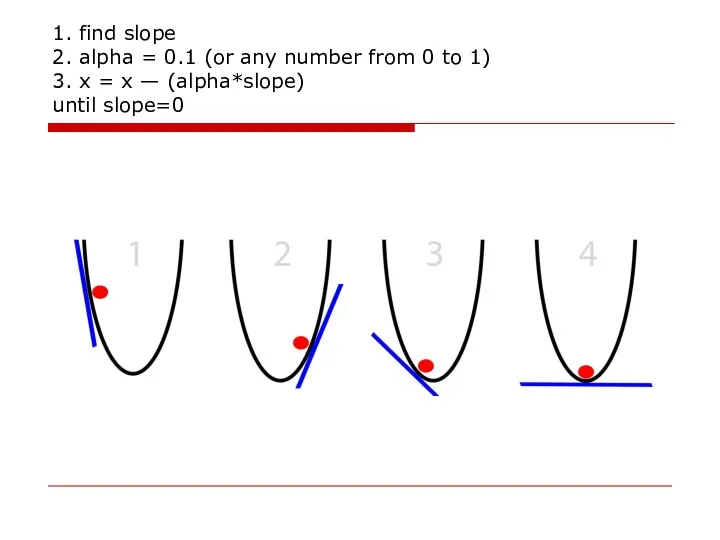
to 1)
3. x = x — (alpha*slope)
until slope=0
Слайд 42The next picture is an activity diagram of the training process with
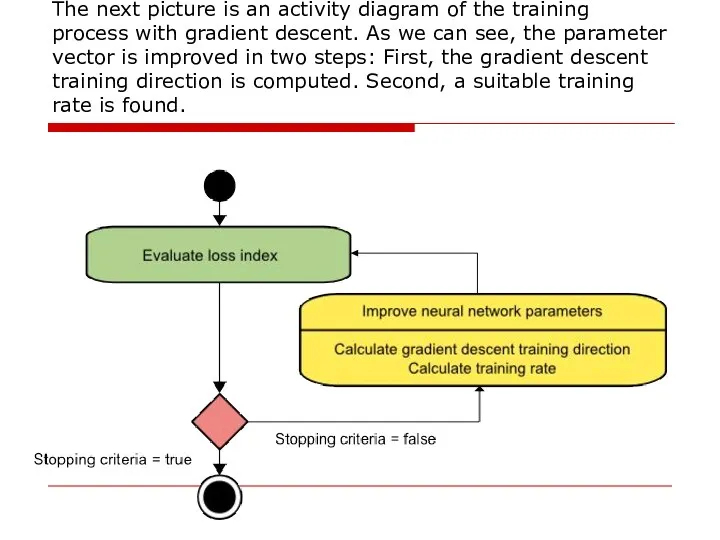
gradient descent. As we can see, the parameter vector is improved in two steps: First, the gradient descent training direction is computed. Second, a suitable training rate is found.
Слайд 43The gradient descent training algorithm has the severe drawback of requiring many
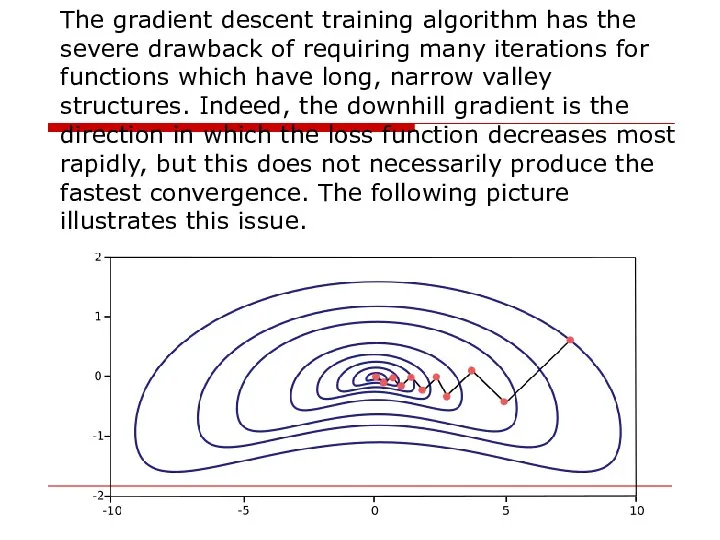
iterations for functions which have long, narrow valley structures. Indeed, the downhill gradient is the direction in which the loss function decreases most rapidly, but this does not necessarily produce the fastest convergence. The following picture illustrates this issue.
Слайд 44Gradient descent is the recommended algorithm when we have very big neural

networks, with many thousand parameters. The reason is that this method only stores the gradient vector (size n), and it does not store the Hessian matrix (size n2).
Слайд 45Optimization algorithm
for Neural network Model
Annealing
Stochastic Gradient Descent
AW-SGD
Momentum
Nesterov Momentum
AdaGrad
AdaDelta
ADAM
BFGS
LBFGS








































 Мероприятия по информированию, вовлечению, анкетированию, отбору и обучению
Мероприятия по информированию, вовлечению, анкетированию, отбору и обучению Питер. 03.04.2017
Питер. 03.04.2017 Лиса в русских народных сказках
Лиса в русских народных сказках Фирмы в экономике
Фирмы в экономике How much do you know about English Christmas?
How much do you know about English Christmas? Функциональные возможности дыхательной системы
Функциональные возможности дыхательной системы Оценочная деятельность учителя
Оценочная деятельность учителя Informace pro studenty
Informace pro studenty Видеоэкология
Видеоэкология Тема: «Живая и неживая природа»
Тема: «Живая и неживая природа» Тепловые явления
Тепловые явления Этапы речевого развития
Этапы речевого развития Писатели и поэты Кубани
Писатели и поэты Кубани Презентацию подготовила библиотекарь МБОУ СОШ №5 Танина С.П
Презентацию подготовила библиотекарь МБОУ СОШ №5 Танина С.П Презентация на тему Family Businesses (Семейный бизнес)
Презентация на тему Family Businesses (Семейный бизнес) Описание объекта
Описание объекта Порядок вступления в силу нормативных правовых актов
Порядок вступления в силу нормативных правовых актов «Женщины Архангельской области: вчера, сегодня, завтра» Н.А. Макарова, председатель РОО «Совет женщин Архангельской области» г
«Женщины Архангельской области: вчера, сегодня, завтра» Н.А. Макарова, председатель РОО «Совет женщин Архангельской области» г Презентация на тему Нефтяная промышленность США
Презентация на тему Нефтяная промышленность США Спасообыденная церковь – прошлое и настоящее
Спасообыденная церковь – прошлое и настоящее Три состояния воды
Три состояния воды Технічне обслуговування верстата HAAS EC-400, який використовується для механічної обробки деталі Люлька PVS71-09.001
Технічне обслуговування верстата HAAS EC-400, який використовується для механічної обробки деталі Люлька PVS71-09.001 Финансовый механизм коммерческого предприятия
Финансовый механизм коммерческого предприятия Волшебное преображение кляксы
Волшебное преображение кляксы Презентация на тему Харганатская средняя общеобразовательная школа
Презентация на тему Харганатская средняя общеобразовательная школа  Русская культура в произведениях русских классиков
Русская культура в произведениях русских классиков Основы государства и права. Законность и порядок
Основы государства и права. Законность и порядок Народные обереговые куклы Козьма и Демьян
Народные обереговые куклы Козьма и Демьян