Независимая переменная Х может принимать любое значение из множества действительных чисел (- ; + ) Область определения функции У Х.
Содержание
- 2. D(x)=R Независимая переменная Х может принимать любое значение из множества действительных чисел (- ∞; + ∞)
- 3. Зависимая переменная У принимает значения из множества действительных чисел (- ∞; + ∞). E(y)=R Область значений
- 4. Точки пересечения графика с осями координат: У Х (0;В) (-В/К;0) с осью ОУ : х=0 ,
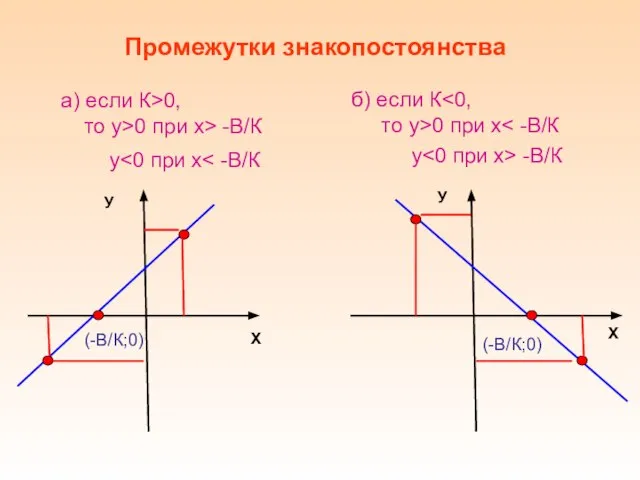
- 5. а) если К>0, Промежутки знакопостоянства б) если К У Х (-В/К;0) то у>0 при х> -В/К
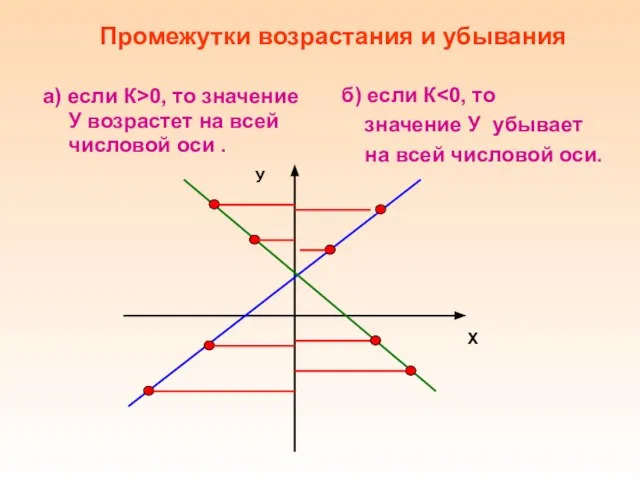
- 6. а) если К>0, то значение У возрастет на всей числовой оси . Промежутки возрастания и убывания
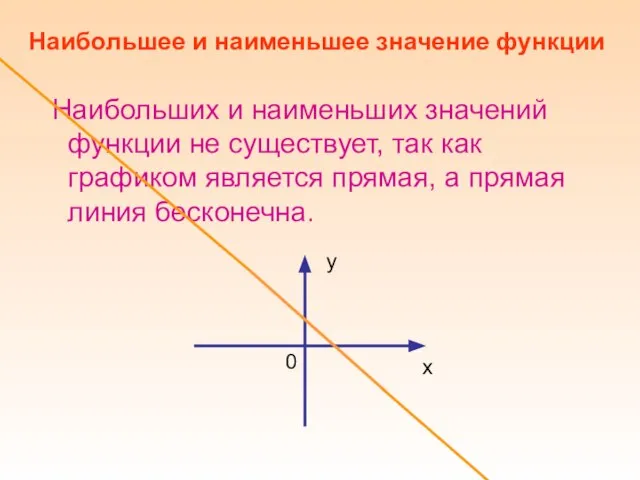
- 7. Наибольших и наименьших значений функции не существует, так как графиком является прямая, а прямая линия бесконечна.
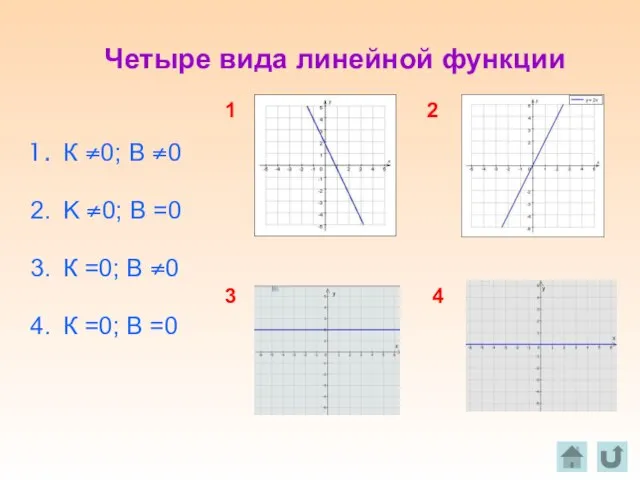
- 8. частные случаи линейной функции
- 9. К ≠0; В ≠0 K ≠0; В =0 К =0; В ≠0 К =0; В =0
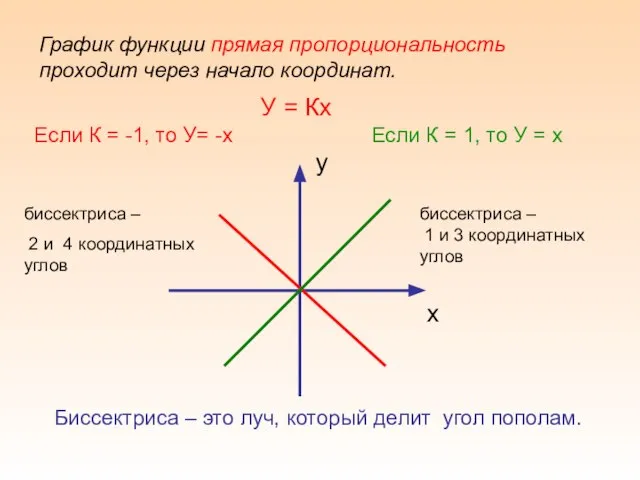
- 10. График функции прямая пропорциональность проходит через начало координат. Если К = -1, то У= -х Если
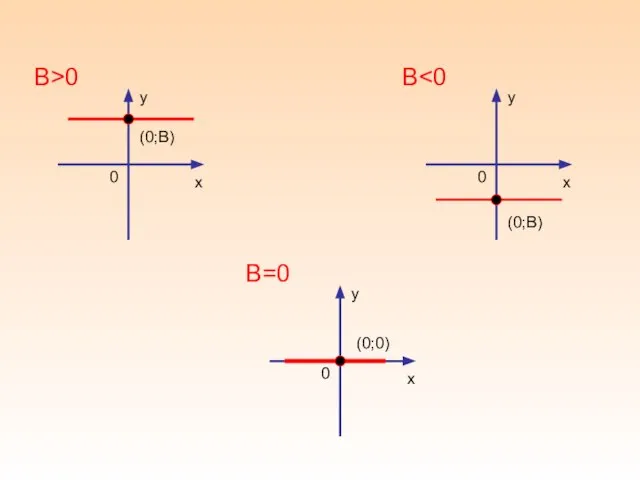
- 11. у х 0 (0;В) В>0 у х 0 (0;В) В у х 0 (0;0) В=0
- 12. Взаимное рассположение графиков линейной функции
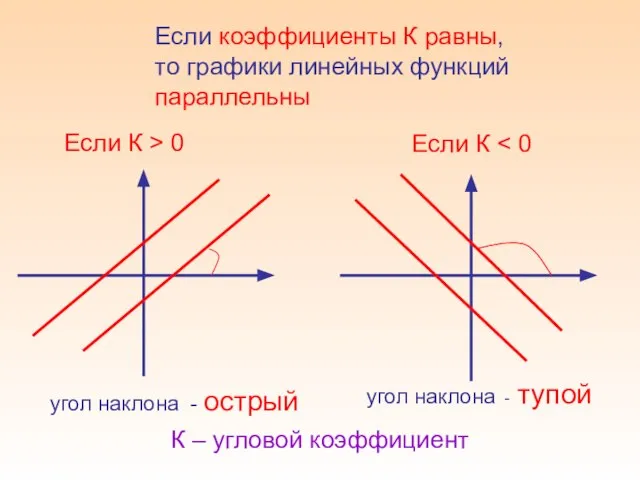
- 13. Если коэффициенты К равны, то графики линейных функций параллельны Если К > 0 угол наклона -
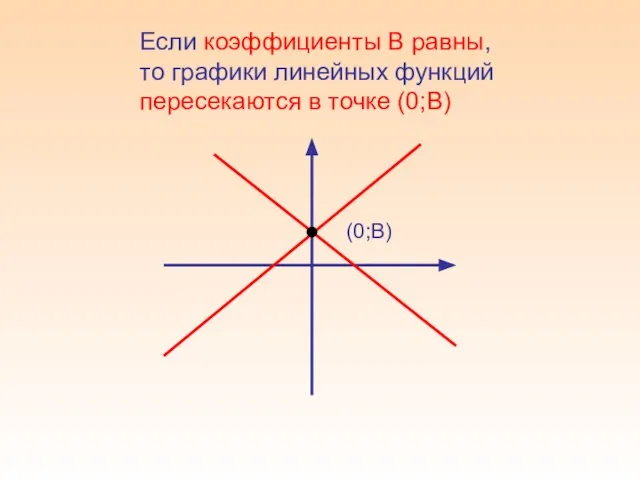
- 14. Если коэффициенты В равны, то графики линейных функций пересекаются в точке (0;В) (0;В)
- 16. Скачать презентацию





 По повести А.М.Горького «Детство»
По повести А.М.Горького «Детство» 65 лет Великой Победе
65 лет Великой Победе Манипуляция и способы противостоять
Манипуляция и способы противостоять Игра по глава Бэла, Тамань, Фаталист произведения Герой нашего времени Лермонтова
Игра по глава Бэла, Тамань, Фаталист произведения Герой нашего времени Лермонтова  Угольная прокуратура
Угольная прокуратура Калибровка длины и диаметра
Калибровка длины и диаметра Prakticheskaya_rabota_1
Prakticheskaya_rabota_1 Особенности ведения деловых переговоров с японцами
Особенности ведения деловых переговоров с японцами Комбинационные логические схемы
Комбинационные логические схемы Презентация на тему Максим Горький
Презентация на тему Максим Горький  Биометрические технологии в криминалистике
Биометрические технологии в криминалистике Asebmblersko programiranje i procesor i8086
Asebmblersko programiranje i procesor i8086 Как продвигать финансовые услуги аудитории интернет-магазина
Как продвигать финансовые услуги аудитории интернет-магазина Болезни, передаваемые половым путем
Болезни, передаваемые половым путем О и а на конце наречий
О и а на конце наречий Презентация на тему Относительные прилагательные
Презентация на тему Относительные прилагательные  ЛЬГОТНОЕ ЛЕКАРСТВЕННОЕ ОБЕСПЕЧЕНИЕ В РОССИИ: системные противоречия и расходование бюджетных средств на меди
ЛЬГОТНОЕ ЛЕКАРСТВЕННОЕ ОБЕСПЕЧЕНИЕ В РОССИИ: системные противоречия и расходование бюджетных средств на меди Хлеб - всему голова и сила
Хлеб - всему голова и сила ОСНОВНЫЕ ИНФОРМАЦИОННЫЕ ПРОЦЕССЫ
ОСНОВНЫЕ ИНФОРМАЦИОННЫЕ ПРОЦЕССЫ Ощущения. Восприятие. Социальное восприятие. Эффекты социального восприятия
Ощущения. Восприятие. Социальное восприятие. Эффекты социального восприятия Наречие 4 класс
Наречие 4 класс Проект www.ram-torg.ru Торговый Интернет-Центр
Проект www.ram-torg.ru Торговый Интернет-Центр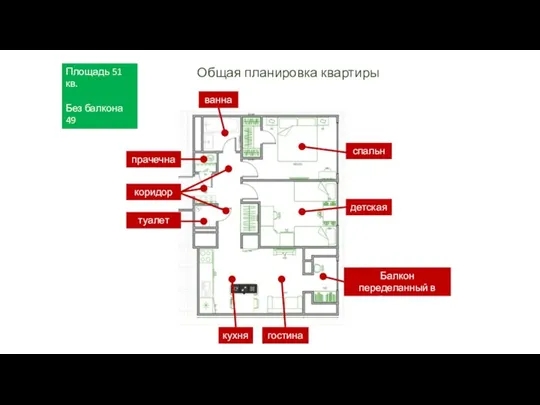 Примерный план ремонта
Примерный план ремонта Классный час «Поговорим о доброте»
Классный час «Поговорим о доброте» Конкуренция и монополия
Конкуренция и монополия  20141019_proektno-issl._deyat-t
20141019_proektno-issl._deyat-t Муниципальное общеобразовательное учреждение «Ахматовская средняя общеобразовательная школа» Тема проекта «Быть всегда всем
Муниципальное общеобразовательное учреждение «Ахматовская средняя общеобразовательная школа» Тема проекта «Быть всегда всем  Имбирное печенье. Новогодний рецепт
Имбирное печенье. Новогодний рецепт