О принципах построения обучаемой системы управления для интеллектуальных роботов на основе динамического ДСМ-метода

3 поколения роботов:
Программные. Жестко заданная программа (циклограмма).
Адаптивные. Возможность автоматически перепрограммироваться (адаптироваться) в зависимости от обстановки. Изначально задаются лишь основы программы действий.
Интеллектуальные. Задание вводится в общей форме, а сам робот обладает возможностью принимать решения или планировать свои действия в распознаваемой им неопределенной или сложной обстановке.
Робот – это машина с антропоморфным (человекоподобным) поведением, которая частично или полностью выполняет функции человека (иногда животного) при взаимодействии с окружающим миром

Архитектура интеллектуальных роботов
Исполнительные органы
Датчики
Система управления
Модель мира
Система распознавания
Система планирования действий
Система выполнения действий
Система управления целями

Роботы «Амур»
Созданы в Творческой научно-технической лаборатории Политехнического музея.
Целью проекта была демонстрация некоторых простейших форм адаптивного поведения, в частности - принципов моделирования условно-рефлекторного поведения, на базе универсального мобильного миниробота. Робот представляет собой автономную тележку, имеющую на борту программируемый контроллер, набор различных датчиков, исполнительные механизмы (эффекторы), модули связи с управляющим компьютером. Робот построен по модульному принципу, что позволяет использовать его компоненты и для других разработок. Именно поэтому робот стал рассматриваться как универсальный полигон, на котором можно отрабатывать решение самых разнообразных управленческих, интеллектуальных и прочих интересных задач.
Адаптивный
Мобильный
Универсальный
Робот
http://railab.ru

Задача – движение по полосе
Добрынин Д.А., Карпов В.Э.
Моделирование некоторых форм адаптивного поведения интеллектуальных роботов.// Информационные технологии и вычислительные системы, Москва, №2, 2006.
роботы АМУР

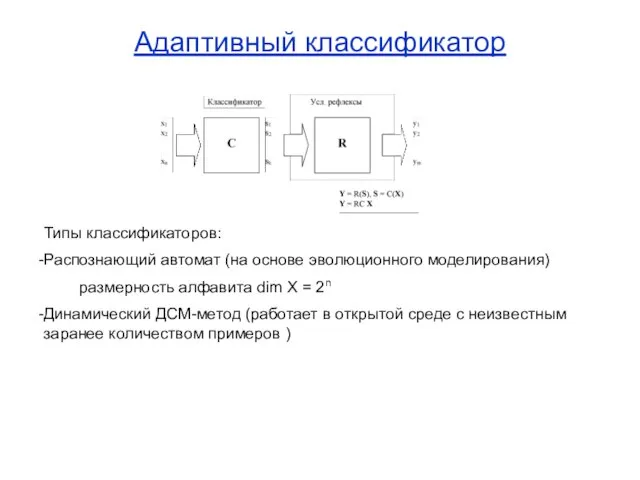
Адаптивный классификатор
Типы классификаторов:
Распознающий автомат (на основе эволюционного моделирования)
размерность алфавита dim X = 2n
Динамический ДСМ-метод (работает в открытой среде с неизвестным заранее количеством примеров )

ДСМ-метод автоматического порождения гипотез получил свое название в честь известного британского философа и экономиста Джона Стюарта Милля. В 1843г. вышла его книга “A System of Logic Ratiocinative and Inductive”, в которой были изложены некоторые принципы индуктивной логики. Новый подход к индуктивной логике был сформулирован профессором В.К. Финном в начале 80-х гг. Первая публикация, в которой были изложены принципы ДСМ - метода, называлась «Базы данных с неполной информацией и новый метод автоматического порождения гипотез», Суздаль,1981г.
ДСМ-метод автоматического порождения гипотез является теорией автоматизированных рассуждений и способом представления знаний для решения задач прогнозирования в условиях неполноты информации.
ДСМ = Джон Стюарт Миль
Виктор Константинович Финн
основатель ДСМ метода

Компоненты ДСМ системы
Истинностные значения {+,-,t,0}
{+} фактическая истина, {-} фактическая ложь, {t} неопределенность, {0} противоречие
Позитивные и негативные примеры (родители)
пример – это сложный объект, состоящий из подобъектов
подобъект (часть объекта) В есть причина наличия (отсутствия) свойства А
Гипотезы о причинах
если объект С содержит некоторый подобъект В, то это причина наличия свойства А
Операции: вложение, пересечение, равенство над множествами
Обучающий алгоритм (учитель)
управляет роботом и порождает примеры из сигналов сенсоров и управления (динамическое порождение базы фактов)

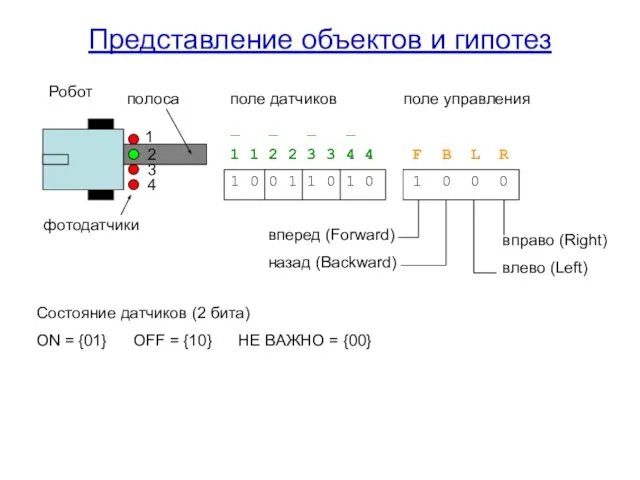
Представление объектов и гипотез
Состояние датчиков (2 бита)
ON = {01} OFF = {10} НЕ ВАЖНО = {00}

Обучающий алгоритм 1
Используем датчик 4
: Simple1 ( -- ? ) Stop Photo4 IF M_TurnLeft
ELSE M_TurnRight THEN
true ;

Обучение для алгоритма 1
Примеры
_ _ _ _
11223344 FBLR
--------------
10101001 0010
10101010 0001
01011010 0001
01010101 0010
01010110 0001
10100101 0010
10010101 0010
10010110 0001
01101010 0001
01101001 0010
01011001 0010
--------------
11 (+)примеров
Минимальные гипотезы
_ _ _ _
11223344 FBLR
--------------
00000001 0010
00000010 0001
--------------
2 (+)гипотезы
Тестовый полигон

На конференции САИТ-2005

Свойства динамического ДСМ
Достаточность обучающих примеров. При наличии представительной выборки обучающих примеров оба метода дают хорошие результаты. Однако в условиях неполноты обучающего множества метод ЭМ дает более устойчивые результаты по сравнению с ДСМ. Это связано прежде всего с характером управления.
Непротиворечивость обучающей выборки. ДСМ, в отличие от ЭМ, не применим в условиях противоречий в обучающих примерах. Такая ситуация может возникать, когда учитель ошибается в оценке состояния датчиков. Ошибки такого типа необходимо отсеивать на этапе формирования обучающих примеров. В ЭМ подобная противоречивость не так критична, т.к. она приводит в худшем случае к неопределенности фенотипического поведения.
Эффективность обучения (скорость). Обучение в ЭМ – принципиально длительный процесс. Для устойчивого обучения методом эволюционного моделирования иногда требуются сотни тысяч тактов. В этом отношении ДСМ-метод обладает несомненным преимуществом - для обучения с помощью ДСМ метода достаточно получить несколько разных обучающих примеров. В экспериментах роботу достаточно было проехать один круг на реальном полигоне чтобы сформировались все необходимые гипотезы.

Свойства динамического ДСМ
Динамическое обучение. Теоретически ЭМ может работать и в открытой среде с неизвестным заранее количеством примеров, практически же это связано с большими вычислительными затратами. Динамический ДСМ метод позволяет эффективно работать с заранее неизвестным количеством примеров при сравнительно небольших вычислительных затратах.
Обучение с учителем. Все рассматриваемые алгоритмы обучения работают с «учителем», который фактически формирует для них представительную обучающую выборку. В качестве «учителя» в проводимых экспериментах выступал внешний алгоритм управления роботом. В принципе, учителем может быть и человек, при условии непротиворечивости выдаваемых им управляющих воздействий.
Требуемые ресурсы. При реализации практических алгоритмов встает проблема ограниченности вычислительных ресурсов автономного робота.Если моделирование эволюции требует весьма больших временных и емкостных затрат, то для работы ДСМ метода достаточно незначительных вычислительных ресурсов, что позволяет разместить программу обучения и управления непосредственно на роботе.

Особенности реализации
небольшая размерность входов и выходов. Как показывает практика, для обучения требуется, всего лишь три-пять входных сигналов и три-четыре выходных;
низкая стоимость системы, за счет использования дешевых 8-ми разрядных микроконтроллеров;
высокое быстродействие;
возможность обучения в изменяющейся рабочей среде;
малое время обучения, возможность учиться в реальном времени;
возможность получить гипотезы в явном виде для дальнейшего анализа. Это свойство ДСМ системы отличает ее от нейронных сетей, для которых невозможно в явном виде выделить причины проявления эффекта.

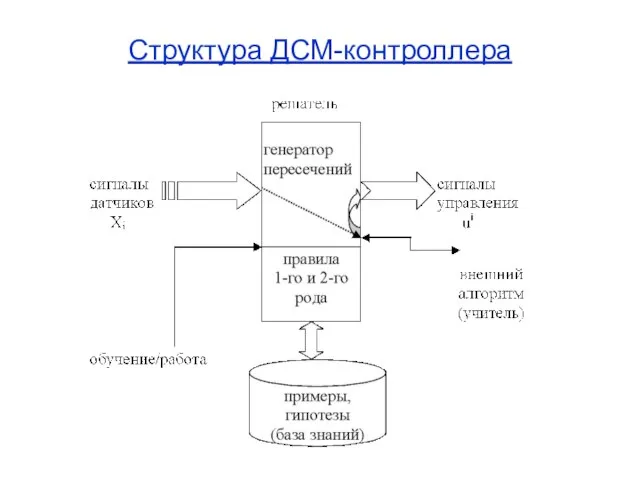
Структура ДСМ-контроллера

Особенности реализации
ДСМ-контроллера
микроконтроллер ATMega128
память программ 128Кбайт
память данных 128Кбайт
Flash память 256Кбайт
тактовая частота 7.3728Мгц
связь с хостом USB 2.0
дополнительный COM порт 230.4 Кбод
линий ввода/вывода 11/4

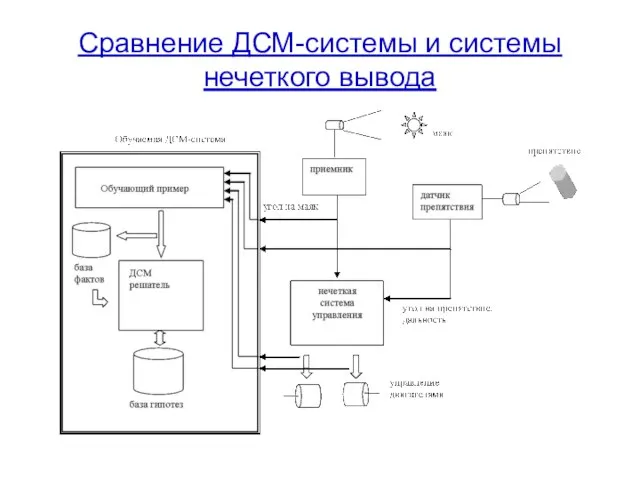
Сравнение ДСМ-системы и системы нечеткого вывода

Результаты обучения
Примеры
_ _ _ _ _ _ _ _ _ _ _ _ _
ddRRrrFFllLLbbRRrrFFllLLBB FBLR
-------------------------- ----
10101010011010101010011010 0010
10101010011010101001101010 0010
10101001101010101001101010 1000
10101001101010101001101010 0010
10101001101010100110101010 1000
10101001101010100110101001 0001
10101010011010101001101001 0001
Минимальные гипотезы
_ _ _ _ _ _ _ _ _ _ _ _ _
ddRRrrFFllLLbbRRrrFFllLLBB FBLR
-------------------------- ----
00101000000000000000000001 0001
00101000000000001000000010 0010
10101001101010000000100010 1000
-------------------------- ----
3 (+)гипотезы
Тестовый полигон

Проблемы применения
Необходимость представления входных данных в виде дискретного множества.
Влияние разрядности входных данных на размерность объектов
если N=210, то требуется вектор из 1024 элементов множества
3. Экспоненциальное снижение быстродействия при увеличении разрядности данных.
4. Необходимо получать выходные сигналы в непрерывном виде (непрерывная система управления).

Переход к «нечеткому ДСМ»
Идея использовать правила нечеткого вывода для ДСМ-метода принадлежит Анашакову О.М. :
Anshakov O, Gergely T. Cognitive Reasoning: A Formal Approach. Springer, 2010
Для перехода к нечетким правилам вывода в ДСМ-методе необходимо осуществить:
замену признаков объекта, которые представляют элементы множества, на элементы нечеткого множества;
переформулировать функции пересечения и вложения для действий над элементами нечеткого множества;
- определить тип целевых свойств и их интерпретацию.

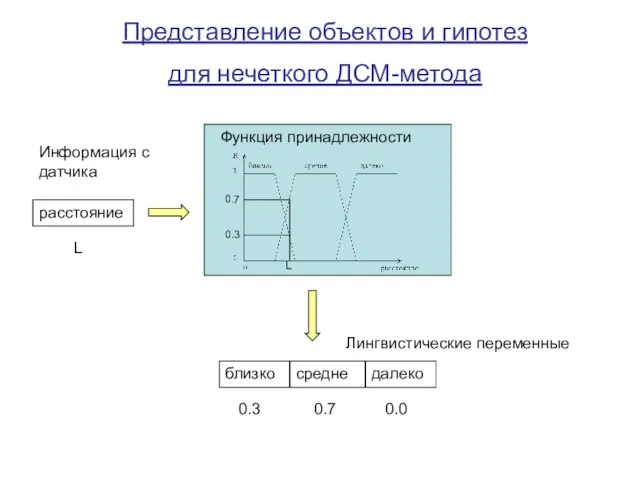
Представление объектов и гипотез
для нечеткого ДСМ-метода

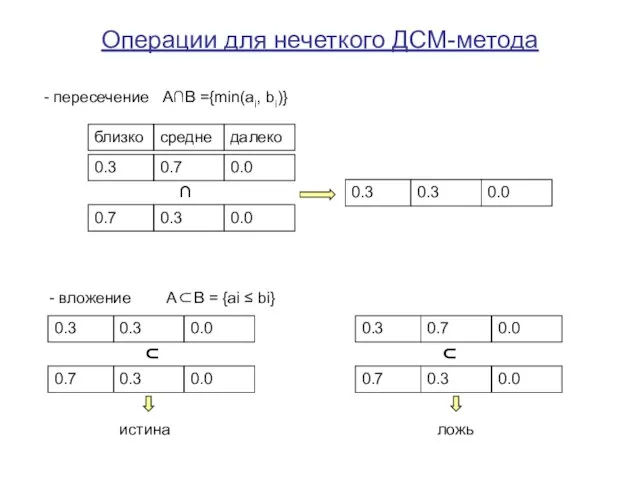
Операции для нечеткого ДСМ-метода

Целевые свойства
атомарные целевые свойства {0, 1} «включить/выключить», «старт/стоп»
непрерывные целевые свойства [0.0, 1.0] необходима операция дефазификации «повернуть на угол α»,
« задать скорость V»