Об энергетическом циклеветровых волн на поверхности океанаГ.С. ГолицынИнститут физики атмосферы им. А.М. Обухова РАНМосква 119017

Ветер возникает вследствие неравномерного нагрева солнечной радиацией
сферической атмосферы планеты. Диссипация кинетической энергии ветра
происходит внутри атмосферы из-за турбулентности и путём трения о
поверхность суши и воды.
Среднее по глобусу поступление энергии Солнца равно
Вт/м Вт/м
В среднем скорость генерации ветра равна скорости её диссипации .
Х. Свердруп (1917) Вт/м
А. Оорт (1963) Вт/м Э. Лоренц (1967, 1970)
КПД по ветру .

Диссипация в пограничном слое:
, (1)
где м), кг/м при С, . Поток импульса от атмосферы к воде
(2)
Приток энергии ветра к поверхности
(3)
Величина измеряется напрямую (И.А. Репина и сейчас у нас), либо извлекается из вертикальных профилей ветра и при стратификациях, близких к
нейтральной, когда масштаб Обухова
м, ,
что соответствует . Однако
С ростом неустойчивости, т.е. при конвекции (Kahma&Calcoen, JGR 1992, Badulin et al,
FM 2007) и с ростом ветра сопротивление растёт, т.е. обмен импульсом и энергией усиливается.

Badulin, Babanin, Zakharov, Resio, JFM 590, 339, 2007:
или , В 2008 (4)
- (5)
- полная энергия волны на единицу площади, - существенная высота волны,
- плотность воды.
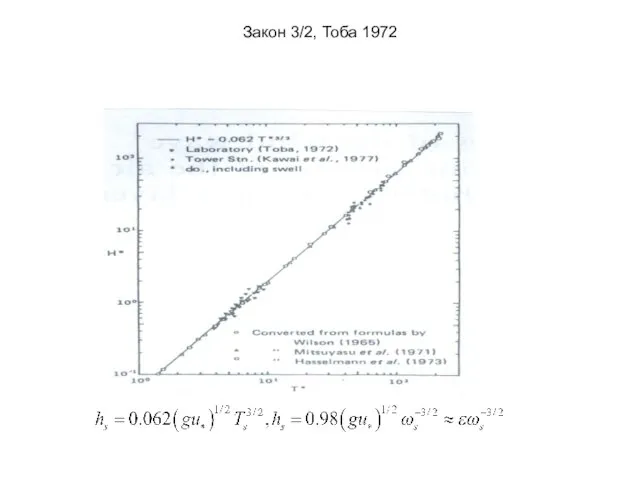
Тоба (1972): (6)
Из (4) – (6) получаем - Китайгородский 1962, КО41.
(7)
КПД по волнам: , (8)

Закон 3/2, Тоба 1972

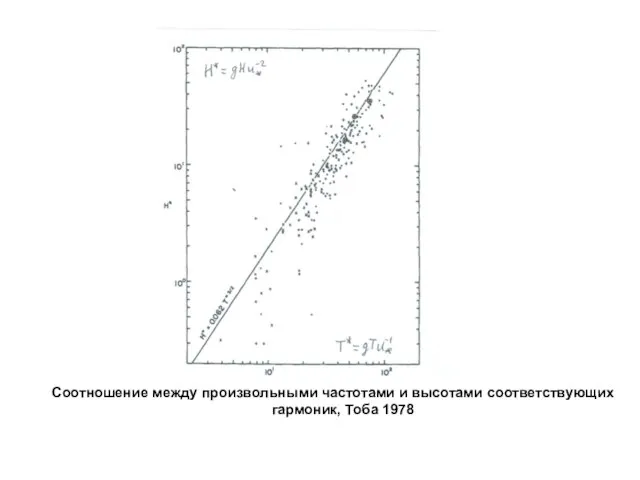
Соотношение между произвольными частотами и высотами соответствующих гармоник, Тоба 1978

Для грубой оценки КПД по волнам примем м/с (Monahan, 2006)
Тогда (или 6.8% при ).
Расчёты 2007 – 4 - 5%.
Согласно (3) и (1) Вт/м
Согласно (8) энергия, идущая на генерацию волн
Вт/м = мВт/м (9)
Учитывая, что океан занимает 71% поверхности земного шара, глобальная
средняя плотность энергии, идущая на генерацию ветровых волн, будет 46 м Вт/м ,
что равно примерно половине геотермического потока из недр Земли, близкого к 90
м Вт/м . Таким образом, на генерацию волн в Мировом океане тратится
т.е. 0.2

Статистика ветра над Мировым океаном
Monahan 2006 a, b, 2008
Функция распределения ветра – Вейбулл
(10)
Моменты
(11)
Оценки (12)
(13)
В среднем глобально м/с, м/с,
что даёт м/с (наиболее вероятная скорость)
Отсюда Вт/м по (1).

Развитие волнения 1.
Возраст волнения
(14)
Безразмерный разгон
(15)
Эволюция пика волнения
(16)
Измерения: Бабанин – Соловьёв
JONSWAP без лаборат. измерений
Kahma&Calkoen, unstable
Kahma&Calkoen, stable
Badulin et al 2007: Далее
Gulev&Hasse 1998 (Donelan Babanin 1.2 – 1.3)

Развитие волнения 2.
Тоба (1987): групповая
(17)
Решение (18)
С учётом (14) – (18) получаем (19)
Все величины выражаем через возраст :
Время разгона (20)
Длина разгона (21)
Период волны
(22)
Длина волны (23)

305
8.4
73.5
21.8
3.9
Бабанин, Соловьёв 1999: ,
Донелан и др. 1985:
Хассельманн и др. 1973:
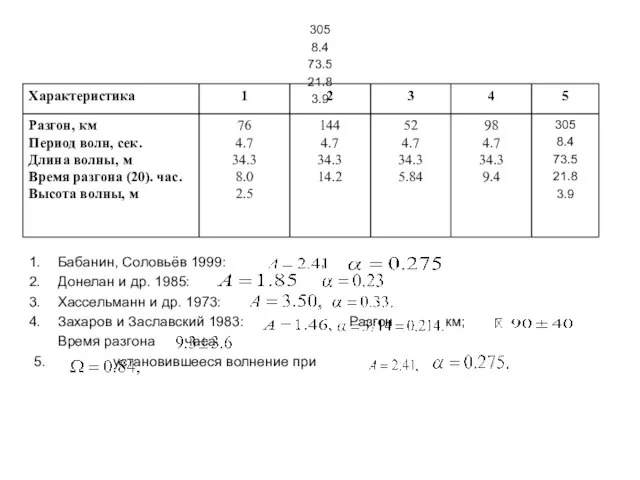
Захаров и Заславский 1983: Разгон км;
Время разгона часа.
5. установившееся волнение при

Энергия волнения
(24)
В то же время
(25)
Используя время разгона (20) и (25), получаем
(26)
При наиболее вероятном ветре м/с,
получаем м. Это надо сравнить со средней
наблюдённой максимальной высотой 2.5 м. По всей видимости наибольшую
погрешность в расчётную формулу (26) вносит значение которое входит как
Французы дают Бадулин и др.
При верхнем пределе получаем м, а при таком пределе
Бадулина: 2.32 м.Точное значение 2.5 м будет при

Зачем всё это?
1. Спутниковые наблюдения за амплитудами волн помогают понять энергетический цикл ветрового волнения. На его поддержание тратится около двух десятых промилле мощности солнечной энергии.
2. Знание возраста волнения и простое его рассмотрение среднего по Мировому океану даёт время развития этого волнения в 8 – 10 часов, разгон порядка 100 км. Близость оцениваемых таким образом амплитуд волн к наблюдённым показывает общую правильность наших представлений о развитии морского волнения. Если бы волнение было установившимся, то его параметры были бы заметно больше.