Объемы наклонной призмы, пирамиды, конуса

План урока
Вычисление объемов тел с помощью определенного интеграла
Объем наклонной призмы
Объем пирамиды
Объем усеченной пирамиды
ОбъемОбъем Объем конуса
ОбъемОбъем Объем усеченного конуса
Вопросы для закрепления

Вычисление объемов тел
Приближенное значение объема тела равно сумме объемов прямых призм, основания которых равны площадям сечений тела, а высоты равны ∆xi = xi – xi – 1
Отрезок [a; b] разбит
на n частей

Вычисление объемов тел с помощью определенного интеграла
Основная формула
для вычисления объемов тел:
Где S(x) – непрерывная функция
на отрезке [a; b].

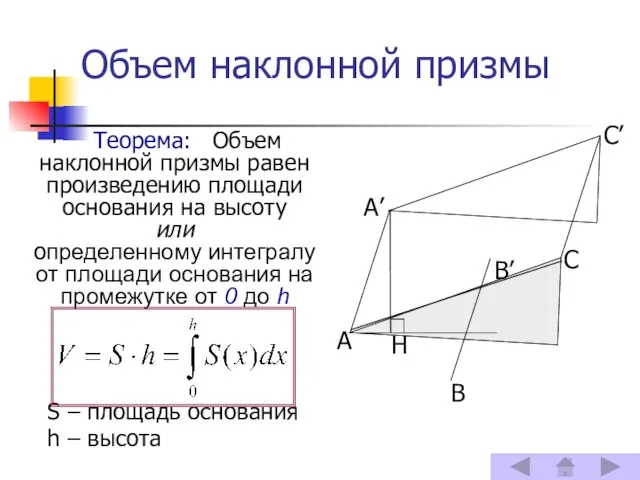
Объем наклонной призмы
Теорема: Объем наклонной призмы равен произведению площади основания на высоту или
определенному интегралу от площади основания на промежутке от 0 до h
S – площадь основания
h – высота

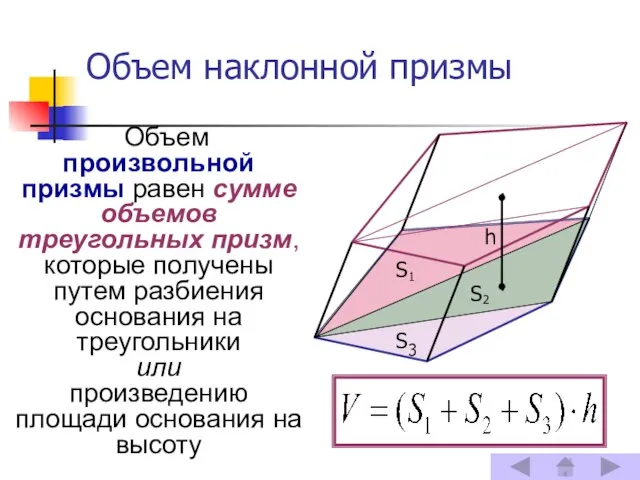
Объем наклонной призмы
Объем произвольной
призмы равен сумме объемов треугольных призм, которые получены путем разбиения основания на треугольники
или
произведению площади основания на высоту

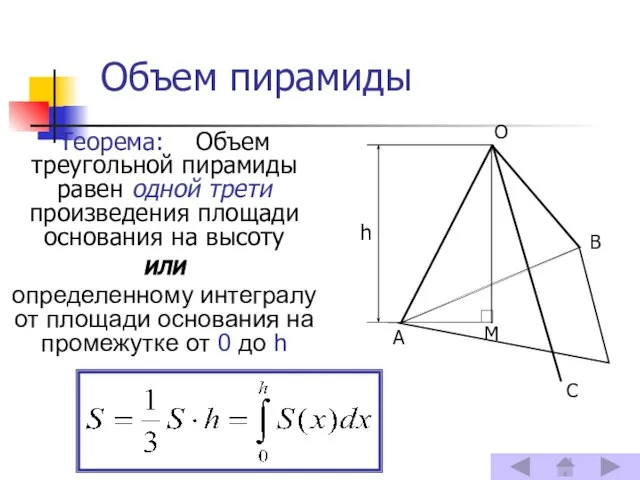
Объем пирамиды
Теорема: Объем треугольной пирамиды равен одной трети произведения площади основания на высоту
или
определенному интегралу от площади основания на промежутке от 0 до h

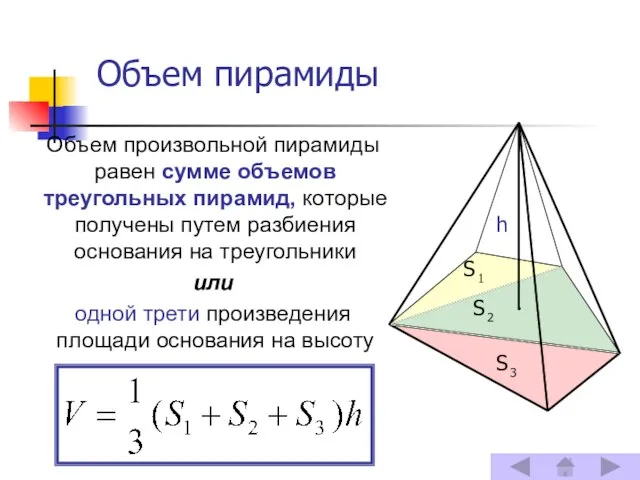
Объем пирамиды
Объем произвольной пирамиды равен сумме объемов треугольных пирамид, которые получены путем разбиения основания на треугольники
или
одной трети произведения площади основания на высоту

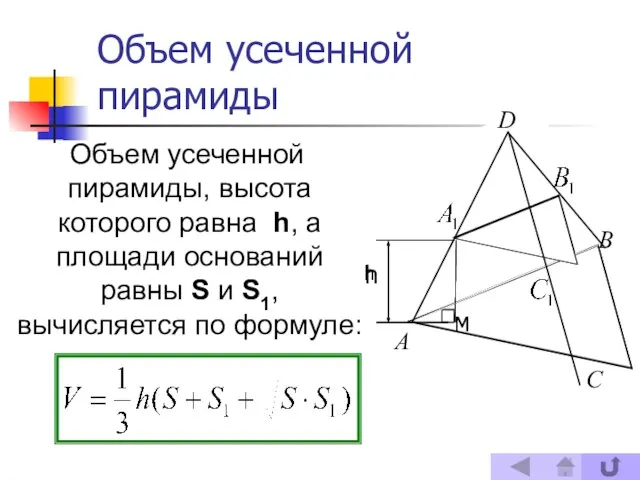
Объем усеченной пирамиды, высота которого равна h, а площади оснований равны S и S1, вычисляется по формуле:
Объем усеченной пирамиды

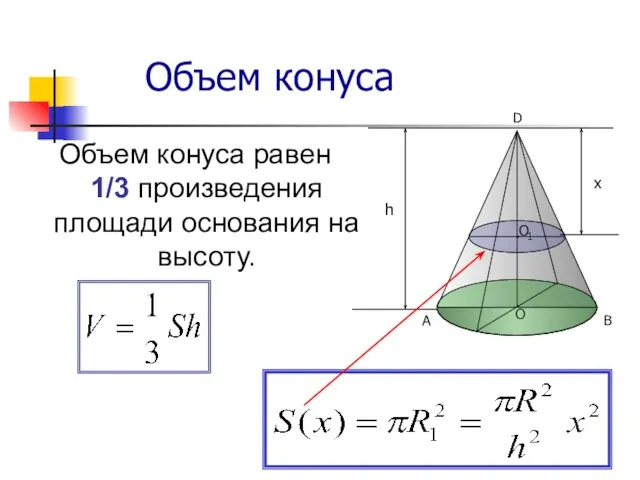
Объем конуса
Объем конуса равен
1/3 произведения площади основания на высоту.

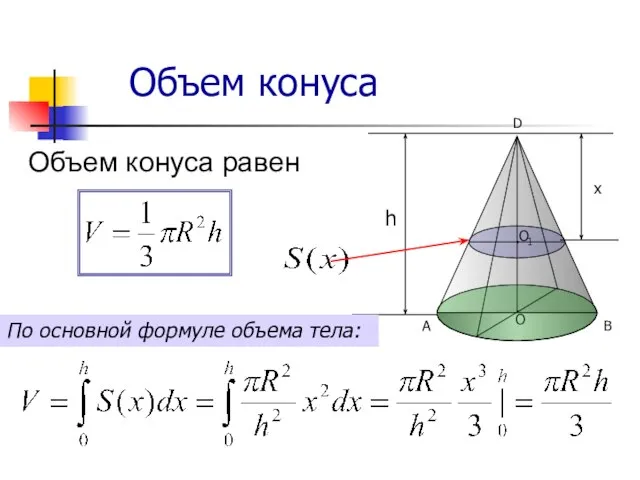
Объем конуса
Объем конуса равен
По основной формуле объема тела:

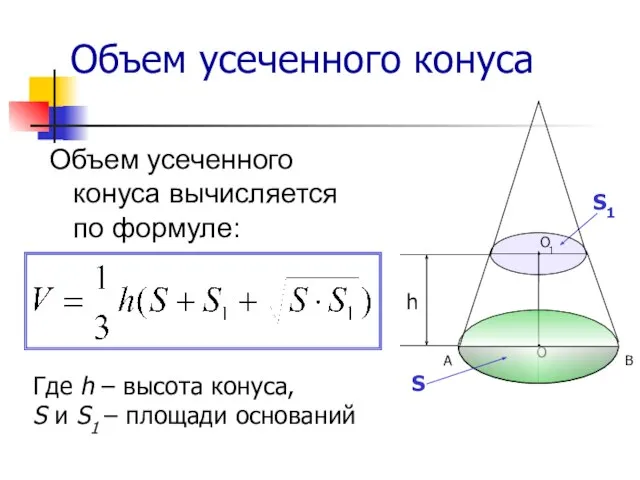
Объем усеченного конуса
Объем усеченного конуса вычисляется по формуле:
Где h – высота конуса, S и S1 – площади оснований