Содержание
- 2. Искажения и артефакты Искажения: -точечные – выбросы, шумы; -линейные - сдвиги линий сканирования по высоте, «двойниковые»
- 3. Искажения Искажение формы ступеньки ВОПГ Интерференционные искажения
- 4. Математическая обработка изображения Задачи: - улучшение качества изображения (снижение уровня шумов, устранение сбоев ступенек, “восстановление” изображения);
- 5. Математическая обработка изображения Пиксельное изображение
- 6. Математическая обработка изображения. Subplane (fine) * - устранение общего наклона изображения: устранение наклона в кадре осуществляется
- 7. Вычитание среднего наклона До процедуры После процедуры Математическая обработка изображения.
- 8. Subplane (fine) * - устранение общего наклона изображения: устранение наклона в кадре осуществляется путем вычитания из
- 9. Медианная фильтрация Усреднение Математическая обработка изображения.
- 10. Математическая обработка изображения Частотная область. Фурье фильтрация. Фурье преобразование - кодирует информацию изображения в терминах частот
- 11. Математическая обработка изображения Фурье фильтрация Приложение Scan Master использует для фильтрации фурье-образа фильтры Баттерворта 1-ого, 2-
- 12. Фурье образ Исходное изображение Использован High Pass Filter Использован Low Pass Filter и X,Y axis Filter
- 13. Построение профиля (Measure | Scan Section) Математическая обработка изображения.
- 14. Построение 3D - изображения Математическая обработка изображения.
- 16. Скачать презентацию
Слайд 2Искажения и артефакты
Искажения:
-точечные – выбросы, шумы;
-линейные - сдвиги линий сканирования по высоте,
Искажения и артефакты
Искажения:
-точечные – выбросы, шумы;
-линейные - сдвиги линий сканирования по высоте,

-двумерные – псевдообъекты, искажения формы ступенек, интерференционные искажения, «двойниковые» изображения;
-обработочные – при проведении некорректных процедур математической обработки изображения.
Артефакты:
-графит - на СТМ-изображении виден лишь каждый второй атом на поверхности, т.е. вместо гексагонов – треугольники;
-изображение иглы (если игла «более плоская», чем особенности на поверхности образца);
-увеличение размеров объектов при «обрастании» иглы;
-зависимость вида изображения от значения туннельного напряжения (для образцов с неоднородной проводимостью поверхности и полупроводников).
Слайд 3Искажения
Искажение формы ступеньки
ВОПГ
Интерференционные искажения
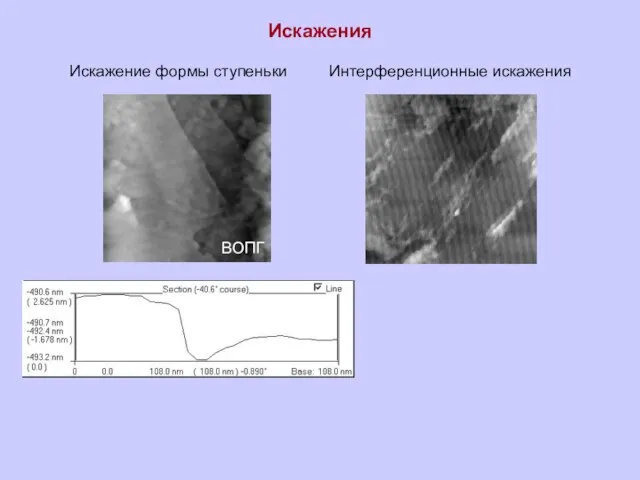
Искажения
Искажение формы ступеньки
ВОПГ
Интерференционные искажения
Слайд 4Математическая обработка изображения
Задачи:
- улучшение качества изображения (снижение уровня шумов, устранение сбоев ступенек,
Математическая обработка изображения
Задачи:
- улучшение качества изображения (снижение уровня шумов, устранение сбоев ступенек,

анализ полученных данных (отделение периодической информации от непериодической, измерение расстояний, параметров шероховатости и т.д.);
представление результатов (выделение объектов, 3-х мерное изображение, цветовая палитра и т.д).
Полезная литература:
Миронов В.Л. Основы сканирующей зондовой микроскопии.-М:Техносфера,2004.144с.
Russ J.C. Computer – assisted microscopy: the measurement and analysis of images. - New York: Plenum Press, 1990. - 451 p.
Розенфельд А. Распознавание и обработка изображений с помощью вычислительных машин. М.: Мир, 1972, - 231 с.
Сканирующая зондовая микроскопия биополимеров. Под редакцией Яминского И.В. М.: Научный мир, 1997. – 86 с.
Учебное пособие по микроскопу СММ-2000, «Шаг за шагом» до получения кадров в СТМ и АСМ. М.: 2005. - 64 c.
Help (программа ScanMaster – Professional scanning & analysis program for SPM).
Слайд 5Математическая обработка изображения
Пиксельное изображение
Математическая обработка изображения
Пиксельное изображение

Слайд 6Математическая обработка изображения.
Subplane (fine) * - устранение общего наклона изображения: устранение наклона
Математическая обработка изображения.
Subplane (fine) * - устранение общего наклона изображения: устранение наклона

Step correction – операция корректирует сбои микроскопа типа «ступенька», проявляющихся в том, что в результате сбоя электроники две соседние строки сканирования могут значительно различаться по высоте: cначала вычисляется средняя высота (среднее Z) всего кадра. Далее кадр обрабатывается построчно. Каждая горизонтальная строка кадра (по X) сдвигается по Z (по высоте) так, чтобы средняя высота строки была равна средней высоте кадра.
Median 2D – медианная фильтрация используется для подавления случайных шумов: медианная фильтрация осуществляется следующим образом. Составляется список значений высоты (или яркости) точки и ее соседей согласно выбранному ядру (например, ядро 3×3 – точка и ее ближайшие соседи: 4 – ортогональных, 4 – диагональных). Список высот сортируется в порядке возрастания. В качестве нового значения высоты данной точки кадра из списка выбирается та высота, номер которой в отсортированном списке ближе всего к номеру, определяемому условием: n=(Nx×Ny-1)×(level/100), где Nx, Ny - размерность матрицы по x, y соответственно, level – уровень медианной фильтрации в % (задается пользователем, по умолчанию – 50).
* названия, принятые в программе Scan Master.
Слайд 7Вычитание среднего наклона
До процедуры
После процедуры
Математическая обработка изображения.
Вычитание среднего наклона
До процедуры
После процедуры
Математическая обработка изображения.

Слайд 8Subplane (fine) * - устранение общего наклона изображения: устранение наклона в кадре
Subplane (fine) * - устранение общего наклона изображения: устранение наклона в кадре

Step correction – операция корректирует сбои микроскопа типа «ступенька», проявляющихся в том, что в результате сбоя электроники две соседние строки сканирования могут значительно различаться по высоте: cначала вычисляется средняя высота (среднее Z) всего кадра. Далее кадр обрабатывается построчно. Каждая горизонтальная строка кадра (по X) сдвигается по Z (по высоте) так, чтобы средняя высота строки была равна средней высоте кадра.
Median 2D – медианная фильтрация используется для подавления случайных шумов: медианная фильтрация осуществляется следующим образом. Составляется список значений высоты (или яркости) точки и ее соседей согласно выбранному ядру (например, ядро 3×3 – точка и ее ближайшие соседи: 4 – ортогональных, 4 – диагональных). Список высот сортируется в порядке возрастания. В качестве нового значения высоты данной точки кадра из списка выбирается та высота, номер которой в отсортированном списке ближе всего к номеру, определяемому условием: n=(Nx×Ny-1)×(level/100), где Nx, Ny - размерность матрицы по x, y соответственно, level – уровень медианной фильтрации в % (задается пользователем, по умолчанию – 50).
* названия, принятые в программе Scan Master.
Математическая обработка изображения.
Слайд 9Медианная фильтрация
Усреднение
Математическая обработка изображения.
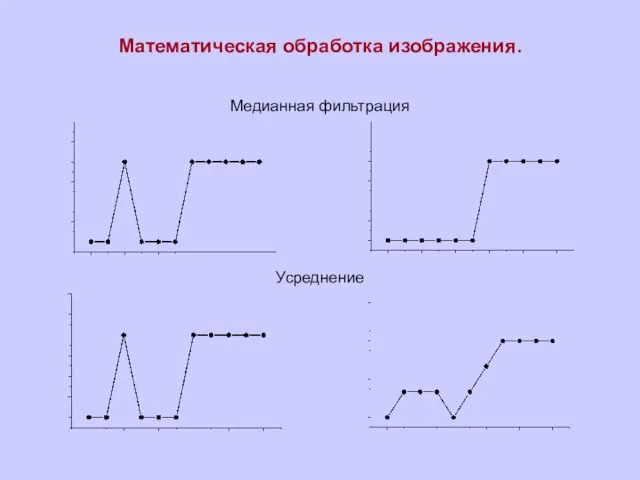
Медианная фильтрация
Усреднение
Математическая обработка изображения.
Слайд 10Математическая обработка изображения
Частотная область. Фурье фильтрация.
Фурье преобразование - кодирует информацию изображения в
Математическая обработка изображения
Частотная область. Фурье фильтрация.
Фурье преобразование - кодирует информацию изображения в

терминах частот в прототипе.
Для изображения, представленного в виде двумерной матрицы значений яркости ƒ(x,y), преобразование рассчитывается в виде:
F(u,ν)= ∫ ∫ ƒ(x,y)exp[-2πi(ux- νy)]dxdy .
Переменные u и ν - частоты.
В частотной области операция действия фильтра:
G(u,ν)= H(u,ν)*F (u,ν),
где F, H и G - частотное преобразование, ядро и результат.
Производное изображение затем восстанавливается методом
обратного преобразования.
Слайд 11Математическая обработка изображения
Фурье фильтрация
Приложение Scan Master использует для фильтрации фурье-образа фильтры
Баттерворта
Математическая обработка изображения
Фурье фильтрация
Приложение Scan Master использует для фильтрации фурье-образа фильтры
Баттерворта

Фильтрация проводится путем умножения Re и Im амплитуд фурье-образа на передаточную функцию фильтра:
new Im(fx,fy) = K(fx,fy)*[old Im(fx,fy)], new Re(fx,fy) = K(fx,fy)*[old Re(fx,fy)]
где K(fx,fy) - передаточная функция фильтра; fx, fy - частоты.
Передаточные функции являются вещественными.
n - порядок фильтра; f02 - квадрат частоты среза фильтра, т.е. частоты, на которой подавление фильтра равно 3 dB; (f0x, f0y) - центр полосы пропускания или подавления полосового фильтра или параметры фильтров осей x,y.
Передаточные функции используемых приложением фильтров
НЧ-фильтр: K1(fx,fy)=1/{1+0.414*[((fx*fx+fy*fy)/f02)**n]}
ВЧ-фильтр: K2(fx,fy)=1/{1+0.414*[(f02/(fx*fx+fy*fy))**n]}
Режекторный (полосовой подавляющий) фильтр:
K3(fx,fy)=1/{1+0.414*[f02/((fx-fx0)**2+(fy-fy0)**2)]**n}+1/{1+0.414*[f02/((fx+fx0)**2+(fy+fy0)**2)]**n }
Полосовой пропускающий фильтр:
K4(fx,fy)=1/{1+0.414*[((fx-fx0)**2+(fy-fy0)**2)/f02]**n}+1/{1+0.414*[((fx+fx0)**2+(fy+fy0)**2)/f02]**n }
НЧ-фильтр с подчеркиванием: K5(fx,fy)= K1(fx,fy)+1
ВЧ-фильтр с продчеркиванием: K6(fx,fy)= K2(fx,fy)+1
Полосовой пропускающий фильтр с подчеркиванием: K7(fx,fy)= K4(fx,fy)+1
Вырезание окрестности оси X: if fx0
В выражении для K3 следует последовательно заменить fy0 на 0, f02 на fy0**2.
Вырезание окрестности оси Y: if fx0>fy0 or abs(fy)>fy0 K9(fx,fy)=1/{1+0.414*(fx0/fx)**(2n)} else K8(fx,fy)=K3(fx,fy)
В выражении для K3 следует последовательно заменить fx0 на 0, f02 на fx0**2.
Нормализация фурье-образа после фильтрации с подчеркиванием K10(fx,fy)=1/2
Слайд 12Фурье образ
Исходное
изображение
Использован
High Pass Filter
Использован
Low Pass Filter
Фурье образ
Исходное
изображение
Использован
High Pass Filter
Использован
Low Pass Filter
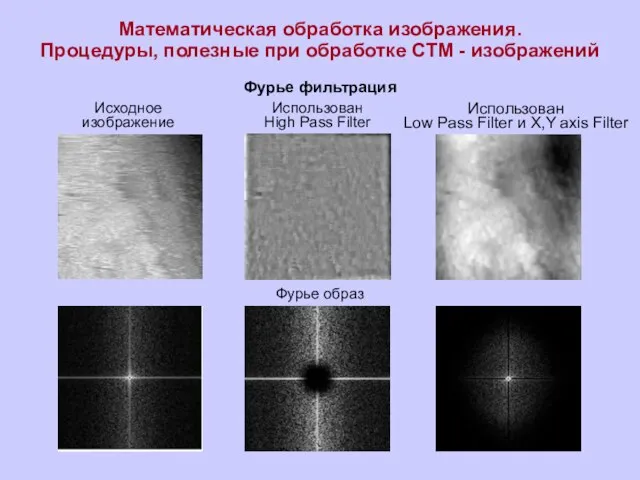
Фурье фильтрация
Математическая обработка изображения.
Процедуры, полезные при обработке СТМ - изображений
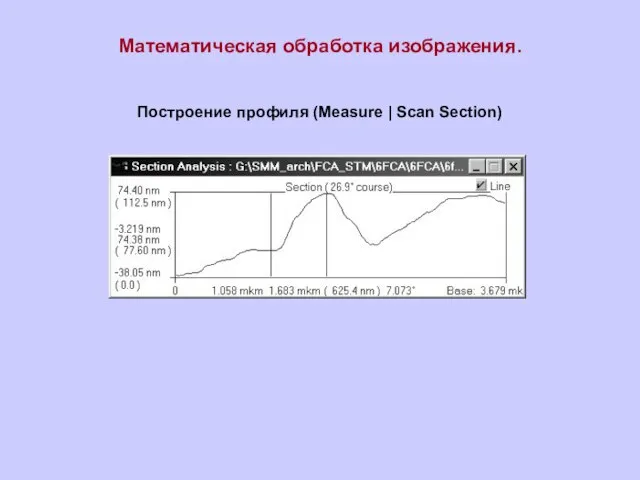
Слайд 13Построение профиля (Measure | Scan Section)
Математическая обработка изображения.
Построение профиля (Measure | Scan Section)
Математическая обработка изображения.
Слайд 14Построение 3D - изображения
Математическая обработка изображения.
Построение 3D - изображения
Математическая обработка изображения.

 Говорим по-английски.
Говорим по-английски. Презентация : «Человек-феномен» Выполнила: Ученица 9 класса Озерова Дарья Руководитель: Учитель обществознания Самуйленко Т.В.
Презентация : «Человек-феномен» Выполнила: Ученица 9 класса Озерова Дарья Руководитель: Учитель обществознания Самуйленко Т.В. К А М П А Н И Я
К А М П А Н И Я Почему планеты разных размеров?
Почему планеты разных размеров? Помоги мышонку и пройди лабиринт
Помоги мышонку и пройди лабиринт Геофизические методы поисков и разведки месторождений полезных ископаемых
Геофизические методы поисков и разведки месторождений полезных ископаемых Алгоритм работы с текстом
Алгоритм работы с текстом Сущность налогов
Сущность налогов Полимерная глина
Полимерная глина «Обломов» — роман-предупреждение
«Обломов» — роман-предупреждение Свойства и состояния воды
Свойства и состояния воды НЕБЛАГОПРИЯТНЫЕ ЛЕКАРСТВЕННЫЕ РЕАКЦИИ
НЕБЛАГОПРИЯТНЫЕ ЛЕКАРСТВЕННЫЕ РЕАКЦИИ Применение солнечной энергетики в городском хозяйстве Москвы
Применение солнечной энергетики в городском хозяйстве Москвы Продукт ActivaScrewTM Канюлированный биодеградируемый винт
Продукт ActivaScrewTM Канюлированный биодеградируемый винт “Обсуждение техники, стратегии и целей присоединения к ВТО: что следует делать Беларуси?” “Анализ практики разрешения споров по
“Обсуждение техники, стратегии и целей присоединения к ВТО: что следует делать Беларуси?” “Анализ практики разрешения споров по Культура Индии
Культура Индии Формирование информационной культуры
Формирование информационной культуры Цивильск
Цивильск Путешествие в сказку
Путешествие в сказку Танк Т-26
Танк Т-26 Топ-5 самых дорогих сортов кофе
Топ-5 самых дорогих сортов кофе Мой Консультант Плюс
Мой Консультант Плюс Муниципальное бюджетное дошкольное образовательное учреждение детский сад № 24
Муниципальное бюджетное дошкольное образовательное учреждение детский сад № 24 Гибкая подводка
Гибкая подводка Виртуальный лабораторный практикум по физике
Виртуальный лабораторный практикум по физике Товарная политика
Товарная политика Презентация на тему Политическая жизнь общества
Презентация на тему Политическая жизнь общества Основы государства и права. Монархия и демократия
Основы государства и права. Монархия и демократия