Обратные тригонометрические функции (11 класс)

Что же такое функция?
Зависимая переменная
Соответствие y = f (x) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой величины х сответсвует определенное значение другой величины у.
Такое соответствие может быть задано различном образом , например : формулой, графически или таблицей.
С помощью функции математически выражаются многообразные количественные закономерности в природе.

Рассмотрим следующие обратные функции:
X = arcsin y
X = arccos y
X = arctg y
X = arcctg y

Обратная функция -
функция, обращающая зависимость, выражаемую данной функцией. Так, если
y =f ( x) — данная функция, то переменная х, рассматриваемая как функция переменной у:
х = j( y), является обратной по отношению к данной функции у = f ( x). Напр., х = есть обратная функция по отношению к y = x3.

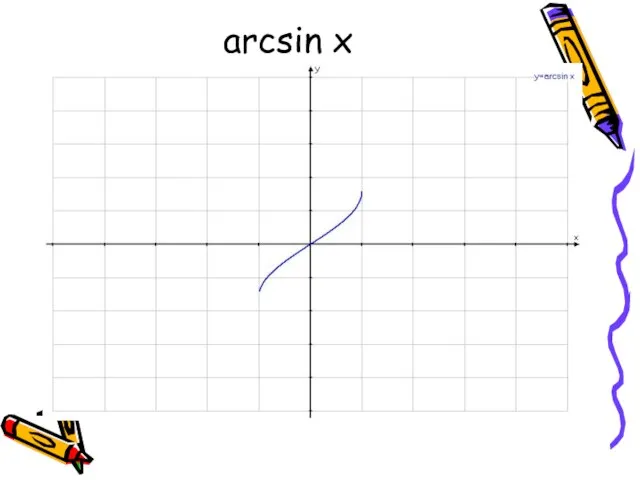
arcsin x
Функция y = sin x, рассматриваемая на промежутке [ -П/2 ; П/2] , имеет обратную функцию, которую называют арксинусом и записывают ч x = arcsin y ,
Свойства этой функции
1) Область определения – промежуток [ -1 ; 1]
2) Множество значений – промежуток [ -П/2 ; П/2]
3) Эта функция нечетная
4) Нули функции: при х = 0
5). Промежутки знакопостоянства
arcsin x> 0, при х ℮ (0;1]
arcsin x< 0 при х ℮ [-1; 0)
6) Функция непрерывна и дифференцируема в каждой точке

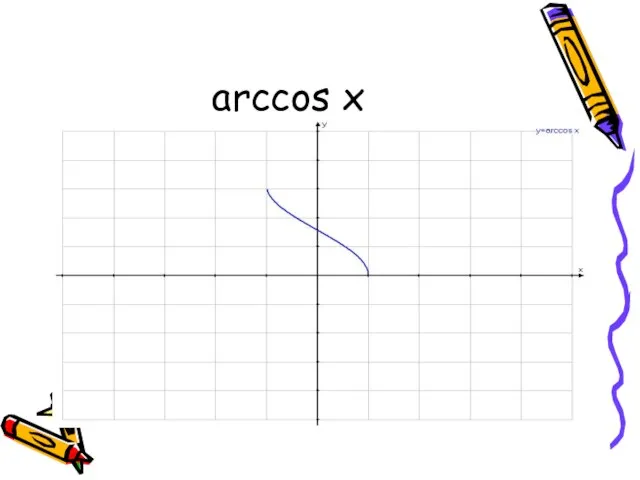
arccos x
Функция у = cos x, рассматриваемая на промежутке [0;П], имеет обратную функцию, которую называют арккосинусом и записывают
x = arccos y
Свойства этой функции
1) Область определения – промежуток [ -1 ; 1]
2) Множество значений – промежуток [ 0 ; П]
3) Эта функция не является ни четной ни нечетной
4) Нули функции: при х = 1
5) Промежутки знакопостоянства arccos > 0, при х ℮ [-1;1)
6) Функция непрерывна и дифференцируема в каждой точке

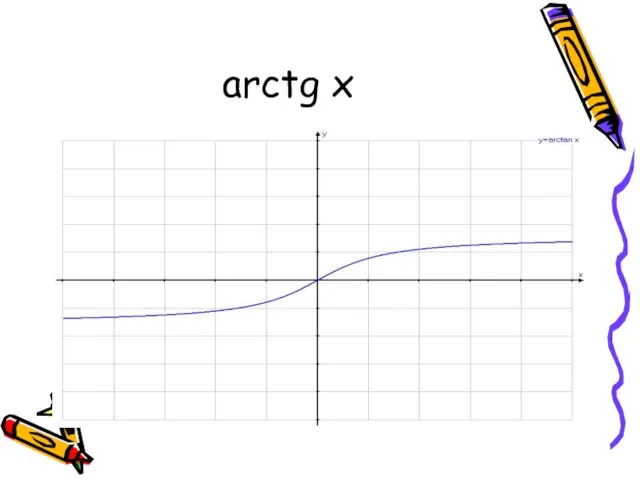
arctg x
Функция y = tg x, рассматриваемая на промежутке (-П/2;П/2), имеет обратную функцию, которую называют арктангенсом записывают
x = arctg y
Свойства этой функции
1) Область определения – вся числовая прямая
2) Множество значений – промежуток (-П/2;П/2)
3) Эта функция является нечетной
4) Нули функции: при х = 0
5) Промежутки знакопостоянства arctg > 0 при х ℮ (0;+∞)
arctg < 0 при х ℮ (-∞;0)
6) Функция непрерывна и дифференцируема при всех х ℮ R

arcctg x
Функция Y = ctg x, рассматриваемая на промежутке (0;П), имеет обратную функцию, которую называют арктангенсом и записывают
x = arcctg y
Свойства этой функции
1) Область определения – вся числовая прямая
2) Множество значений – промежуток (0;П)
3) Эта функция не является ни четной ни нечетной
4) Функция положительна при всех х ℮ R
5) Функция непрерывна и дифференцируема при всех х ℮ R

arcsin x

arccos x

arctg x