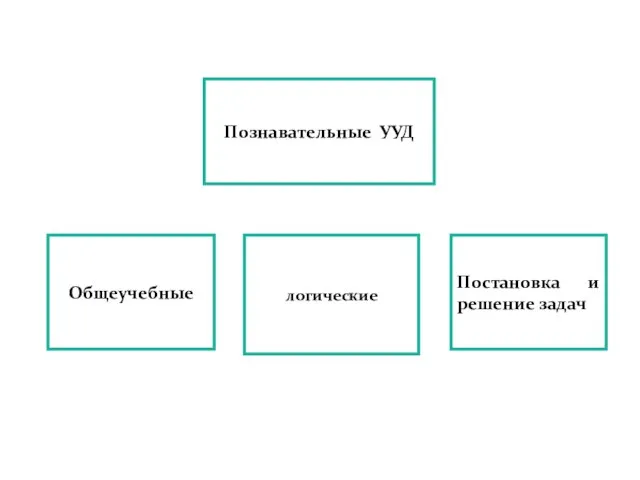
Слайд 2Общеучебные
Постановка и решение задач
Познавательные УУД
логические
Слайд 3
Особую группу общеучебных
универсальных действий составляет знаково-символические действия, основным показателем развития которых

в начальной школе является овладение моделированием
Слайд 4 Знаково – символическое моделирование - преобразование объекта из чувственной формы в

модель, где выделены существенные характеристики объекта( пространственно- графическая или знаково- символическая)
Преобразование модели с целью выявления общих законов, определяющих данную предметную область.
Обучение по действующим программам любых учебных предметов предполагает применение разных знаково-символических средств (цифры, буквы, схемы, и т.д.) .
Моделирование включает в свой состав знаково-символические действия: замещение, кодирование, декодирование.
Учащиеся должны освоить системы социально принятых знаков и символов.
Учащиеся должны принять идею означивания и понять ее на произвольно созданной символике.
Слайд 5 Мой опыт показывает, что составление сложных выражений из простых вызывает определенные

сложности у учащихся. Мы с учениками стали думать, как бы найти прием-помощник для того, чтобы связать эти выражения в математическую цепочку.
Слайд 6 Для решения текстовых задач используются модель-рисунок, краткая запись, рисунок-схема, таблица, схема анализа
Целесообразно

кооперативное использование различных способов моделирования задачи при решении сложных составных задач на несколько действий, введения нового типа задач.
Слайд 7 Составить равенство:
28 + 10 =

Слайд 12 Мы используем понятия «выражение», «значение выражения» знаки действий, понимаем действия I и

II ступеней, обозначаем порядок выполнения действий с использованием цифр:
79 – 5х 2 + 6: 3 – 16 и находим ответ, решая по действиям .
По учебнику Аргинской в 3- 4 классах приводятся задания, когда даны простые выражения ( суммы, разности, произведения, частного). По заданию данные выражения нужно связать по значению и составить сложные выражения. Например, № 86 учебника «Математика», 3 класс, часть II.
В указанном задании из выражений необходимо составить сложное выражение:
63 + 18 81 : 9 73 - 67 4 х 6 24 + 9
После того, как дети нашли значение каждого выражения, составили сложное выражение :
( 63 + 18) : 9 + 4 х ( 73 - 67)
Слайд 13 Далее решение примеров при определении того, что общего и чем отличаются
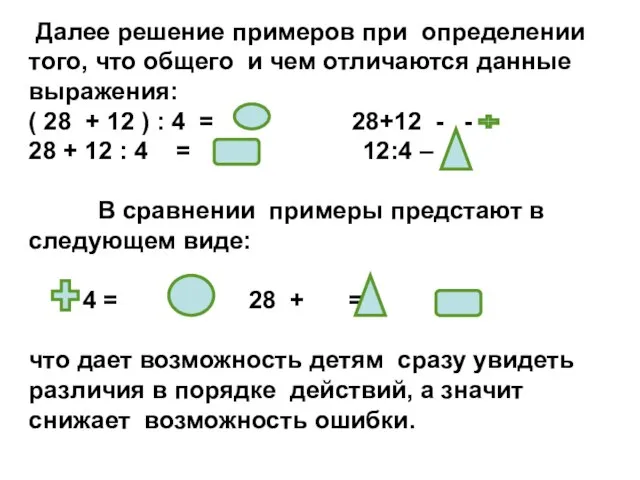
данные выражения:
( 28 + 12 ) : 4 = 28+12 - -
28 + 12 : 4 = 12:4 –
В сравнении примеры предстают в следующем виде:
: 4 = 28 + =
что дает возможность детям сразу увидеть различия в порядке действий, а значит снижает возможность ошибки.
Слайд 14 Классическая методика, разработанная самими авторами учебника Аргинской и Кормишиной предлагают следующую

схему решения сложных выражений, которую также используют дети при выполнении задания, т.е. реализуется принцип вариативности выбора детьми способа выполнения задания:
Слайд 15 Мы же использовали эти знаки для определения порядка выполнения действий в

сложном выражении, который имеют двоякое смысловое значение: подразумевая под знаком и выражение, значение которого нужно найти и само получившееся значение
Слайд 16 Приняв такой принцип составления программы решения, можно использовать различные виды заданий,

дифференцировав их уровень :
Задания на нахождение вычитаемого : 1) 78 - = 70 , задав при этом знак действия.
Слайд 17Применение учащимися знаково-символического анализа сложного выражения привело к следующей схеме решения примера:
















 МОУ гимназия № 1
МОУ гимназия № 1 Промышленное производство аммиака
Промышленное производство аммиака Серебряный век в искусстве
Серебряный век в искусстве Алгоритм отработки лидов
Алгоритм отработки лидов Презентация на тему Атмосферные осадки
Презентация на тему Атмосферные осадки  Сочетание устойчивого развития и сохранения исторической памяти
Сочетание устойчивого развития и сохранения исторической памяти Социальная коммуникация. Лекция 1
Социальная коммуникация. Лекция 1 Анкета клиента на проведение аудита
Анкета клиента на проведение аудита Псковская судная грамота: общая характеристика
Псковская судная грамота: общая характеристика Первичная обработка кролика
Первичная обработка кролика Конструктивное построение предметов
Конструктивное построение предметов Презентация на тему Основная позиция пальцев на клавиатуре
Презентация на тему Основная позиция пальцев на клавиатуре  Политическая социализация
Политическая социализация ОСНОВНЫЕ ПАРАМЕТРЫ ИССЛЕДОВАНИЯ R-TGI (РОССИЙСКИЙ ИНДЕКС ЦЕЛЕВЫХ ГРУПП) Ежеквартальное измерение особенностей потребления товаров,
ОСНОВНЫЕ ПАРАМЕТРЫ ИССЛЕДОВАНИЯ R-TGI (РОССИЙСКИЙ ИНДЕКС ЦЕЛЕВЫХ ГРУПП) Ежеквартальное измерение особенностей потребления товаров, Легковое такси
Легковое такси ЕГЭ по литературе: сдаю или сдаюсь?
ЕГЭ по литературе: сдаю или сдаюсь? Курсовой проект: Проектирование железобетонных конструкций многоэтажного здания
Курсовой проект: Проектирование железобетонных конструкций многоэтажного здания «Значение имени Маргарита
«Значение имени Маргарита Значение страхования жизни и пенсионного обеспечения для украинского общества
Значение страхования жизни и пенсионного обеспечения для украинского общества Интервальное голодание. Меню
Интервальное голодание. Меню Здоровый ребёнок-Здоровое будущее!!!
Здоровый ребёнок-Здоровое будущее!!! Административно-правовые основы управления. Часть II
Административно-правовые основы управления. Часть II Такие знакомые и неизвестные нам пчелы
Такие знакомые и неизвестные нам пчелы Эй, народ честной, одевай кафтаны цветастые, платья красные и айда гулять на ярмарку – на народ посмотреть, да себя показать!!! А на я
Эй, народ честной, одевай кафтаны цветастые, платья красные и айда гулять на ярмарку – на народ посмотреть, да себя показать!!! А на я Коми кывйысь урок .Чачаяс вузасянiнын. Урок коми языка. В магазине игрушек
Коми кывйысь урок .Чачаяс вузасянiнын. Урок коми языка. В магазине игрушек ДОЖДЬ
ДОЖДЬ Гранулоцитарный колониестимулирующий фактор (G-CSF, Г-КСФ): молекулярная биология, биотехнология, производство лекарственных форм, к
Гранулоцитарный колониестимулирующий фактор (G-CSF, Г-КСФ): молекулярная биология, биотехнология, производство лекарственных форм, к Презентация на тему Круговорот веществ и превращение энергии в экосистеме
Презентация на тему Круговорот веществ и превращение энергии в экосистеме