О некоторых работах П. Е. Эльясберга в НИИ – 4 в период с 1949 по 1953 годы Их роль в развитии теории полета баллистических и крылатых р

ЧАСТЬ I
Работы П. Е. в области баллистики ракет дальнего действия

Основные направления
Работы, связанные с составлением таблиц стрельбы для первой отечественной баллистической ракеты Р – 1.
Метод совместной обработки результатов измерений с методическими (детерминированными) и случайными погрешностями.
Приложение к определению инструментальных погрешностей систем управления дальностью (ИГ – 1) и боковым отклонением (БРК).
Работы по вариационным задачам и их влияние на решение проблемы оптимизации траекторий баллистических и крылатых ракет.

ЧАСТЬ II
Крылатые ЛА с ЖРД и второе рождение
одной классической задачи

1. Немного истории
От «Большой птицы» Леонардо да Винчи
до первых крылатых ракет

500 лет назад
Леонардо да Винчи о «Большой птице»
266.
Большая птица первый полет начнет со спины исполинского Лебедя, наполняя вселенную изумлением, наполняя молвой о себе все писания,- вечной славой гнезду, где она родилась.
267.
С горы, от большой птицы получившей имя, начнет полет знаменитая птица, которая наполнит мир великой о себе молвой.
Леонардо да Винчи.
Избранные произведения, том первый.
Academia, Москва – Ленинград, 1935, с. 173.

300 лет назад
Иоганн Бернулли. Задача о брахистохроне
Чтобы пробудить интерес у любителей такого рода вопросов и побудить их к более охотной попытке решения данной проблемы, я сообщаю им, что эта проблема не может быть сведена к пустой умственной спекуляции, лишенной какого – либо практического значения, как это может кому – либо показаться. На самом деле эта проблема представляет большой практический интерес не только для механики, но также для других дисциплин, что может показаться невероятным.
Iohannis Bernulli
M. D. Problem novum, ad cujus solutionem Mathematical invitatur. Acta erudito – rium, 1696 (Jun.).
Задача о брахистохроне (в современных терминах)
Найти уравнение линии, двигаясь вдоль которой в однородном гравитационном поле материальная точка переместится из заданной точки А в заданную, расположенную ниже ее, точку В в минимальное время.

60 лет назад
Первые самолеты с ЖРД с наземным стартом
Экспериментальный самолет с ЖРД БИ – 1,
СССР, 1942, Григорий Бахчиванджи
Истребитель- перехватчик Ме – 163, Германия, 1943;
СССР, 1945,
Марк Галлай

60 лет назад
Первые крылатые ракеты
Экспериментальная крылатая ракета А-4B, созданная на базе баллистической ракеты А-4, Германия, 1944
Дальний бомбардировщик с ЖРД (крылатая ракета) Е. Зенгера (проект), Германия, 1944

2. Второе рождение задачи о брахистохроне
50-ые – 60-ые годы

Экспериментальные самолеты с ЖРД с воздушным стартом
Максимальная скорость 1.650 миль/час (М = 2.4) на высоте 70.000 футов
Максимальная скорость 4.520 миль/час на высоте 354.200 футов
Экспериментальный самолет с ЖРД X1-A, 1953, США, Чак Игер
(сброс с самолета Б-29)
Экспериментальный самолет с ЖРД X-15, 1959 – 1968, США, Нейл Армстронг (впоследствии – первый человек, ступивший на поверхность Луны (сброс с самолета Б-52)

Задачи об оптимальных траекториях
набора высоты крылатыми ЛА с ЖРД
Задача об оптимальной траектории набора высоты ЛА с ЖРД
Синтезировать программу управления, обеспечивающую максимум конечной скорости Vk на заданной высоте hk при заданном законе изменения тяги и заданных значениях начальной скорости V0, высоты h0, начальной массы μ0, и конечной массы μk.
Эквивалентная задача
Обеспечить максимум μk при заданных V0, h0, Vk, hk.,что соответствует минимуму расхода топлива μk - μ0 и минимуму времени набора заданной высоты.
Соответствующая вариационная задача –
Обобщенная задача о брахистохроне
Найти функцию y(x), обеспечивающую экстремум функционала
zk = F(x, y(x), y’ (x)) при граничных условиях
y = y0 при x = x0 ; y = yk при x = xk. (1)
Примечание: В случае вырожденной задачи искомая экстремаль принадлежит классу кусочно-гладких функций

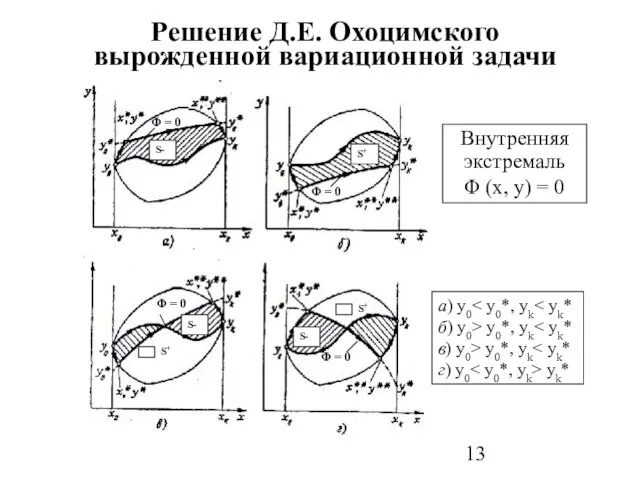
Решение Д.Е. Охоцимского
вырожденной вариационной задачи
S+
Φ = 0
Внутренняя экстремаль
Φ (x, y) = 0
а) y0< y0*, yk< yk*
б) y0> y0*, yk< yk*
в) y0> y0*, yk< yk*
г) y0< y0*, yk> yk*
S-
Φ = 0
S+
Φ = 0
S+
Φ = 0
S-
S-

Решение вырожденной вариационной задачи, продолжение
Выражения первых двух вариаций и конечного приращения функционала zk в случае вырожденной вариационной задачи
(2)
Необходимые условия сильного максимума функционала zk
(3)
Достаточные условия абсолютного максимума функционала zk
(4)

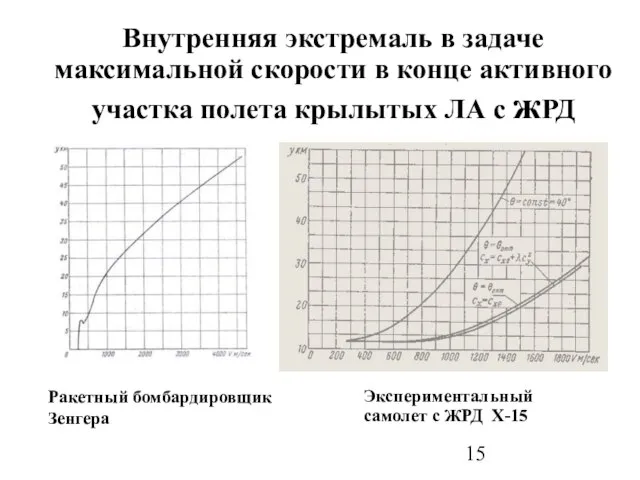
Внутренняя экстремаль в задаче максимальной скорости в конце активного участка полета крылытых ЛА с жРД
Экспериментальный самолет с ЖРД X-15
Ракетный бомбардировщик Зенгера

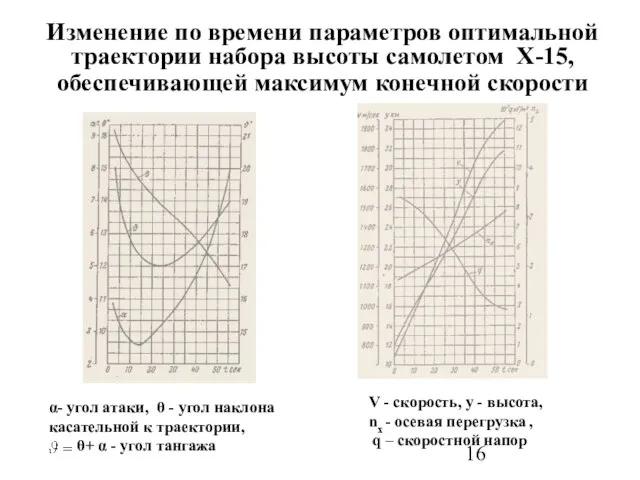
Изменение по времени параметров оптимальной траектории набора высоты самолетом X-15, обеспечивающей максимум конечной скорости
α- угол атаки, θ - угол наклона касательной к траектории,
θ+ α - угол тангажа
V - скорость, y - высота,
nx - осевая перегрузка ,
q – скоростной напор

3. От «Шаттла» и «Бурана» к крылатым ЛА с ЖРД
с наземным и воздушным стартом
70-ые – 80-ые годы– наше время
(проекты)

Новый «Зенгер»
An Advanced European Two-Stage Space Transport System
SÄNGER

Наземный старт с платформы на магнитной подвеске, разгоняемой линейным приводом
Side view of the HIMES/LMAC launch system

Воздушный старт
L’avion a haute altitude White Knight emporte le SpaceShipOne.
La vaisseau spatial, lance a partir de 15 km, doit s’elever a 100 km d’altitude