Содержание
- 2. Высказывание в логике является аналогом выражения в арифметике: В алгебре чисел из чисел при помощи операций
- 3. Обозначения логических значений А, В – логические переменные, которые могут иметь значение ИСТИНА (И), ЛОЖЬ (Л).
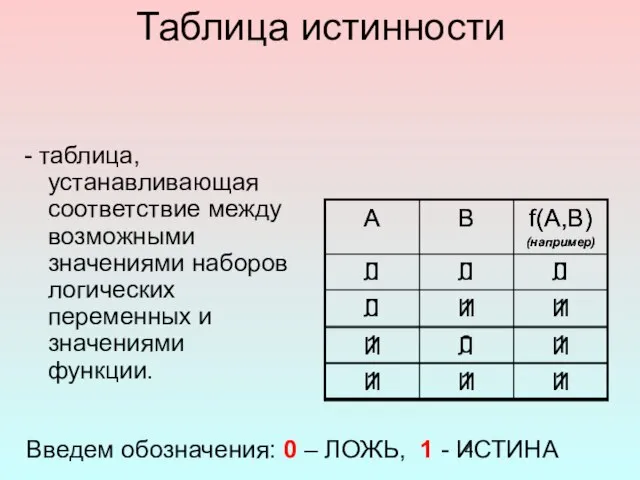
- 4. Таблица истинности - таблица, устанавливающая соответствие между возможными значениями наборов логических переменных и значениями функции. Введем
- 5. Основные логические операции И – логическое умножение, ИЛИ – логическое сложение, НЕ – логическое отрицание. Простые
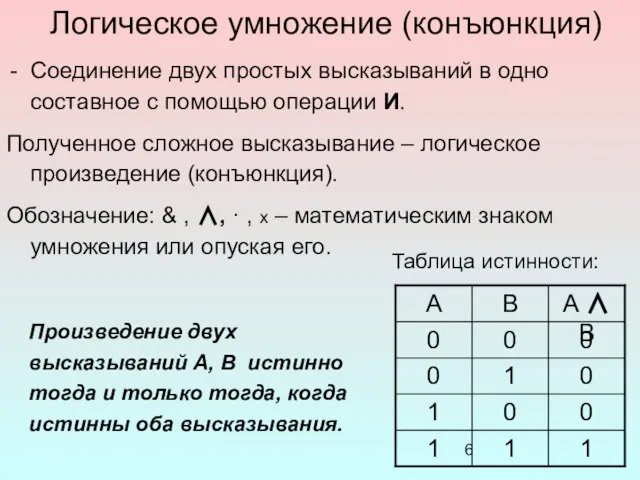
- 6. Логическое умножение (конъюнкция) Соединение двух простых высказываний в одно составное с помощью операции И. Полученное сложное
- 7. Например: «Солнце светит и нет дождя» Обозначим: А = «Солнце светит», В = «нет дождя». С
- 8. Логическое сложение (дизъюнкция) Союз ИЛИ в обиходе применим в двух различных значениях: в исключающем и неисключающем
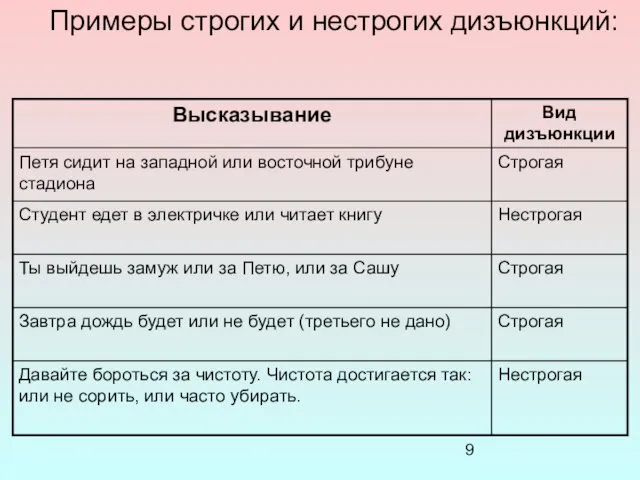
- 9. Примеры строгих и нестрогих дизъюнкций:
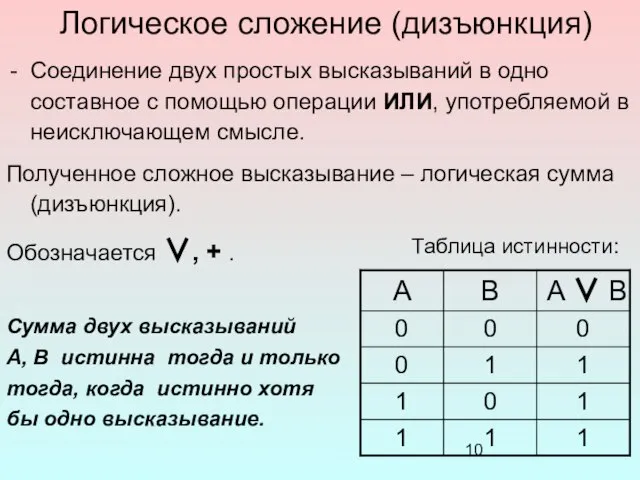
- 10. Логическое сложение (дизъюнкция) Соединение двух простых высказываний в одно составное с помощью операции ИЛИ, употребляемой в
- 11. Например: «Студент едет в электричке или читает книгу» Обозначим: А = «Студент едет в электричке», В
- 12. Логическое отрицание (инверсия) Присоединение частицы НЕ к сказуемому данного высказывания А, или словосочетания «неверно, что» ко
- 13. Например: «Число 5 является делителем числа 30» Обозначим: А = «Число 5 является делителем числа 30»,
- 14. При образовании сложных высказываний из простых можно использовать несколько логических операций. Приоритет выполнения операций (если нет
- 15. Операции инверсия, конъюнкция и дизъюнкция являются основными операциями алгебры логики и называются булевыми операциями. Существуют другие
- 16. Эквивалентность Обозначение: ~ Логическая связка «ТОГДА И ТОЛЬКО ТОГДА» Сложное высказывание А ~ В (А эквивалентно
- 17. Например: А = Площадь квадрата больше единицы, В = Сторона квадрата больше единицы. Их соединение эквивалентностью:
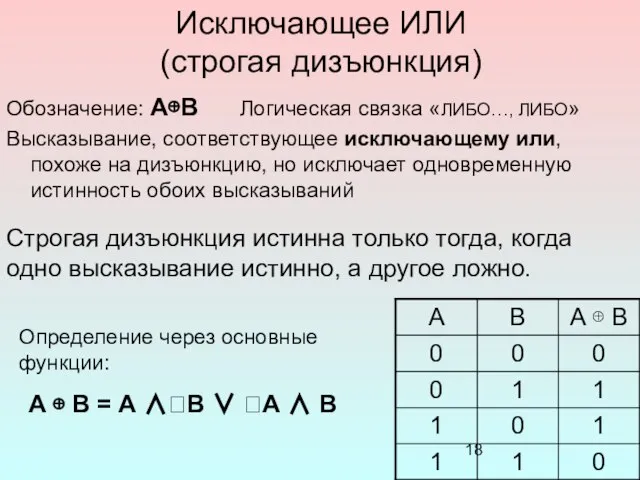
- 18. Исключающее ИЛИ (строгая дизъюнкция) Обозначение: А⊕В Логическая связка «ЛИБО…, ЛИБО» Высказывание, соответствующее исключающему или, похоже на
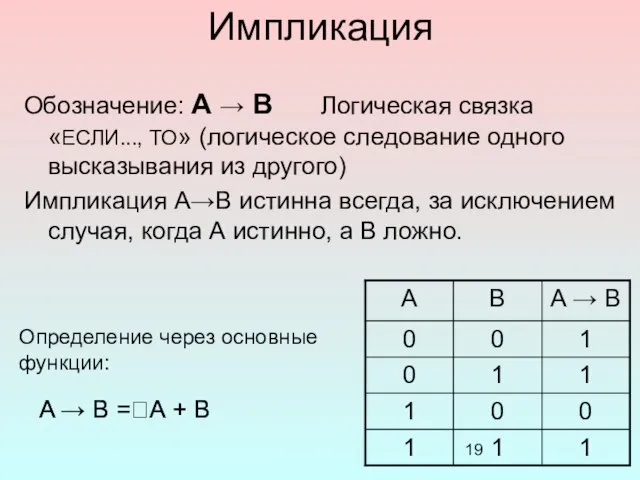
- 19. Импликация Обозначение: А → В Логическая связка «ЕСЛИ..., ТО» (логическое следование одного высказывания из другого) Импликация
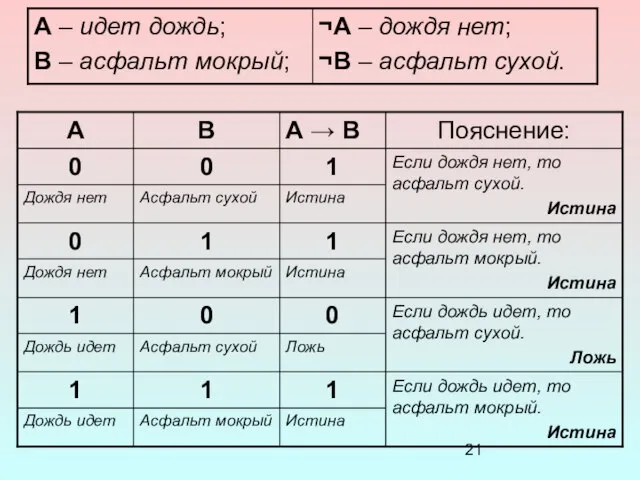
- 20. Например: А = На улице дождь. В = Асфальт мокрый. A → B = «Если на
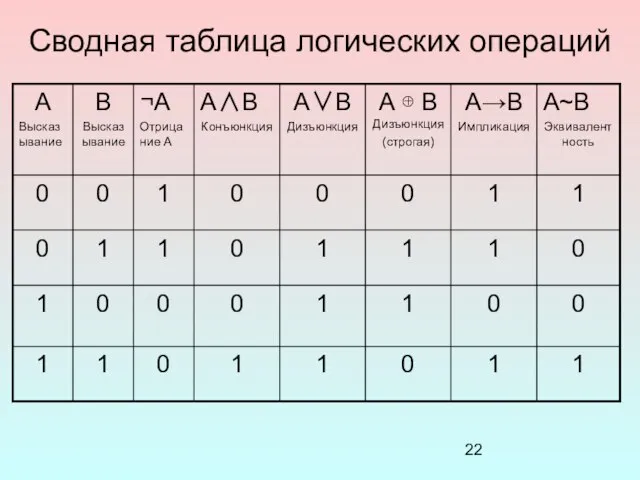
- 22. Сводная таблица логических операций
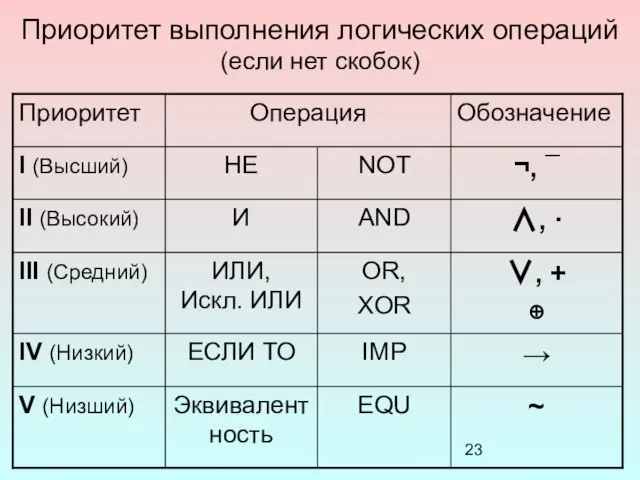
- 23. Приоритет выполнения логических операций (если нет скобок)
- 24. Например: ¬A∨B∧C→C∧A~B ⊕ C⊕A (((¬A)∨(B∧C))→(C∧A))~((B⊕C)⊕A) 1 3 2 5 4 8 6 7 ¬A∨B∧C→C∧A~B ⊕ C⊕A
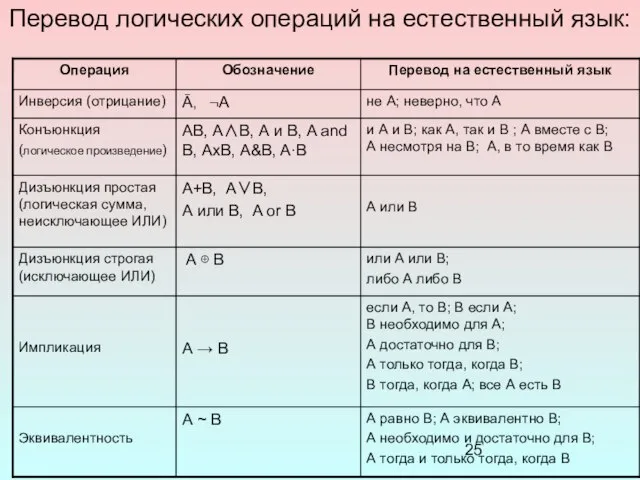
- 25. Перевод логических операций на естественный язык:
- 26. Пример: Изобразить в виде формулы суждение: «Я обязательно поеду на футбольный матч, если достану билет или
- 27. Введем обозначения: Б – я достану билет; Б – я не достану билет; П – меня
- 28. Сложное высказывание: «Я достану билет или меня пригласит товарищ и не будет дождя» Б ∧ ¬Д
- 29. Составление таблицы истинности для сложного высказывания. (Например: А·(В + С).) Правило: Число исходных столбцов равно числу
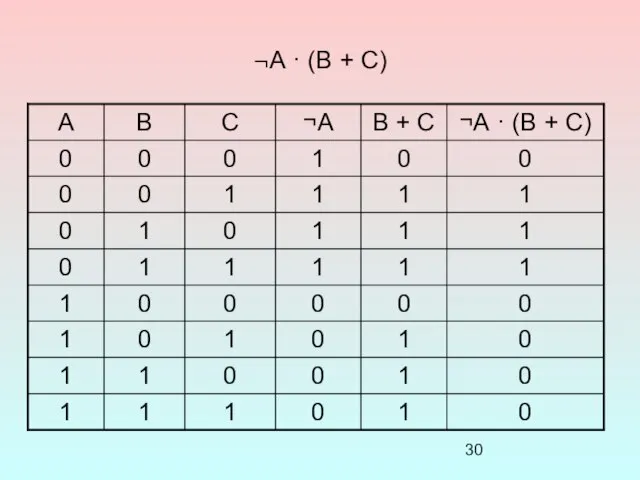
- 30. ¬А · (В + С)
- 31. Самостоятельная работа 1. Составить таблицу истинности: М = Б ·¬Д + П ·¬Д 2. Изобразить в
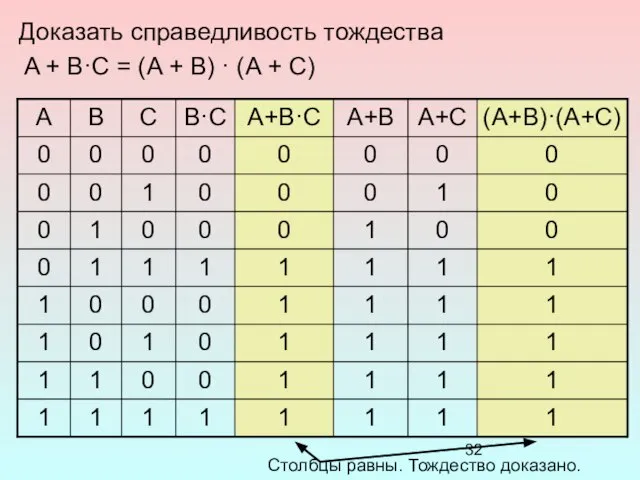
- 32. Доказать справедливость тождества A + B·C = (A + B) · (A + C) Столбцы равны.
- 34. Скачать презентацию



















 Проповедь Христа
Проповедь Христа KIBERMAKON VA DIN taqdimot
KIBERMAKON VA DIN taqdimot Троекуровский Свято – Димитриевский Иларионовский женский монастырь
Троекуровский Свято – Димитриевский Иларионовский женский монастырь Лекция 10. Электоральное поведение.
Лекция 10. Электоральное поведение. Формирование Древнерусского государства
Формирование Древнерусского государства ПРОЕКТИРОВАНИЕ ТРАНСПЛАНТАЦИОННЫХ РЕФОРМПолтерович В.М (ЦЭМИ РАН и РЭШ, Москва)Июль 2008
ПРОЕКТИРОВАНИЕ ТРАНСПЛАНТАЦИОННЫХ РЕФОРМПолтерович В.М (ЦЭМИ РАН и РЭШ, Москва)Июль 2008 Управление интегрированными коммуникациями. Когда?
Управление интегрированными коммуникациями. Когда? Филиал московского университета имени С.Ю. Витте в г. Сергиев Посад, для выпускников 9 классов
Филиал московского университета имени С.Ю. Витте в г. Сергиев Посад, для выпускников 9 классов Жизнь Ломоносова -
Жизнь Ломоносова - Образ семьи в русской живописи ( ко Дню семьи, любви и верности)
Образ семьи в русской живописи ( ко Дню семьи, любви и верности) Презентация на тему Импрессионизм в живописи
Презентация на тему Импрессионизм в живописи  Информация и знания 5-7 класс
Информация и знания 5-7 класс Проект Праздник в хату
Проект Праздник в хату Россия Крым ИВГПУ (фотографии)
Россия Крым ИВГПУ (фотографии) Государственная собственность в РФ. История и современность
Государственная собственность в РФ. История и современность shopping_list__food
shopping_list__food Сендвич-панели
Сендвич-панели  Пишем проект!
Пишем проект! Этикетка ампул
Этикетка ампул Click to edit Master title style Click to edit Master subtitle style
Click to edit Master title style Click to edit Master subtitle style  Нашим мамам. Фотоальбом
Нашим мамам. Фотоальбом Петровский завод в цифрах
Петровский завод в цифрах Эффективная реклама для обеспеченной аудитории
Эффективная реклама для обеспеченной аудитории Нюрнбергский процесс.Уроки истории.
Нюрнбергский процесс.Уроки истории. Романтизм в искусстве
Романтизм в искусстве Решение задач
Решение задач готика
готика Презентация на тему Вода - главный источник жизни
Презентация на тему Вода - главный источник жизни