Описание дефектов кристаллической структуры в рамках теории упругости

В настоящем разделе рассматриваются задачи, в которых концентрацию дефектов считается малой, то есть можно предполагать, что дефекты образуют в матрице слабый раствор и их взаимодействие мало.
Для ряда задач удобно воспользоваться моделью сплошной среды и пренебречь деталями кристаллического строения изучаемого твердого тела. В этом случае решение можно искать в рамках теории упругости.

Основные положения механики сплошной среды
При континуальном описании кристалла исходным понятием служат векторы абсолютных смещений, определяемых в каждой точке среды в некоторый момент времени t:
При деформации координата точки среды перемещаются: x0 → x=x0 +Δx
относительная линейная деформация среды

– локальная объемная относительная деформация – дилатация.
Определение: Основной геометрической характеристикой деформированного состояния среды является симметричный тензор относительной деформации

Определение: Пусть – сила, приложенная в точке А, принадлежащей единичной площадке, ориентированную в соответствии с нормалью , которая и задает ориентацию площадки. Тензор напряжений связывает ориентацию площадки с компонентами силы.
Пусть в среде задана система координат.
В случае, если твердое тело подвержено гидростатическому давлению, напряжения равны
В любом тензоре напряжений можно выделить его гидростатическую часть:
Тогда оставшийся тензор есть тензор-девиатор

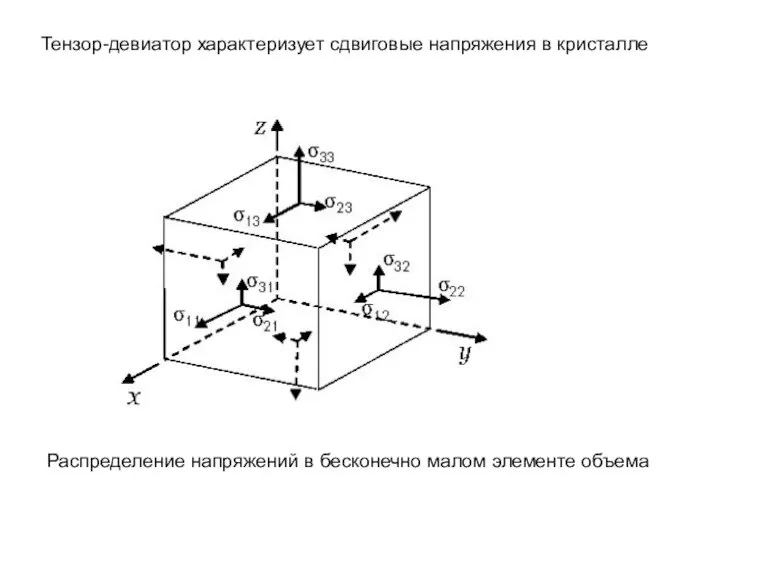
Тензор-девиатор характеризует сдвиговые напряжения в кристалле
Распределение напряжений в бесконечно малом элементе объема

Закон Гука
Тензор называется тензором упругих модулей.
Общее количество компонент тензора
.
кубический кристалл
Обозначения свернутых индексов:

Изотропная конденсированная среда
Т.е. для описания изотропной среды нужно всего два индекса:
, G.
Закон Гука для изотропной среды примет вид
где коэффициент
коэффициент G – модуль сдвига.
- модуль объемного сжатия,

Связи различных коэффициентов упругости изотропной среды:

ЗАКОН ГУКА В ОБОБЩЕННОМ ВИДЕ
Сначала рассмотрим следующие условия:
- температура постоянная и однородная по образцу;
- среда изотропная;
- внутренних дефектов в среде нет.
Пусть F – свободная энергия среды. По определению, напряжения в среде есть
Любой тензор относительной деформации можно, как и тензор напряжений, представить в виде суммы гидростатической и девиантной частей:

Разложим добавку к свободной энергии, обусловленную деформацией, по малым смещениям, точнее по квадратам гидростатической и девиантной частей тензора относительной деформации
где коэффициенты G и K -коэффициенты разложения.
В дальнейшем мы их будем называть G – модулем сдвига,
K – модулем объемного сжатия

СВОБОДНА ДЕФОРМАЦИЯ!?
В представленном виде закона Гука не учитывается возможность возникновения свободной деформации, не приводящей к появлению напряжения.

Таким примером является свободное термическое расширение.
Будем считать недеформированным состояние тела при отсутствии внешних сил при некоторой температуре T0. Если тело находится при температуре , то даже в отсутствии внешних сил оно будет деформировано в связи с наличием теплового расширения.
Поэтому в разложение свободной энергии F(T) будут входить не только квадратичные, но и линейные по тензору деформации члены.
Из компонент тензора второго ранга можно составить всего только одну линейную скалярную величину – сумму его диагональных элементов . Далее, будем предполагать, что коэффициент при пропорционален разности (T-T0). В этих предположениях для свободной энергии системы получим:

Дифференцируя F по , получим тензор напряжений:
При свободном тепловом расширении тела (при отсутствии внешних сил) внутренние напряжения должны отсутствовать, т.е.

Точечные дилатационные дефекты
Определенный вид точечных дефектов кристалла также, по сути, является внутренними центрами дилатации (расширения), но локализованными.
При однородном пространственном распределении таких точечных дилатационных дефектов, эффект их воздействия на тело может рассматриваться по аналогии с тепловым расширением и, следовательно, под действием дефектов тело также деформируется без возникновения напряжений.
Свободная деформация возникает также и при введении точечных дефектов в твердое тело:
– концентрация дефектов, ω - дилатационный объем дефектов.

Общий вид уравнений в абсолютных смещениях.
Рассмотрим уравнение теории упругости с учетом действия дефектов на расстояниях меньших, чем среднее расстояние между отдельными дефектами n-1/3.
В условиях статического равновесия
здесь вектор fi описывает плотность действующих на кристалл объемных сил, а тензор связан с деформациями законом Гука.
Под fi понимаются внешние силы, действующие внутри среды, в частности, это могут быть силы, действующие со стороны отдельных дефектов, выражение для которых пока нам не известно.

Для получения вида f получим уравнение в абсолютных смещения

Данное уравнение должно решаться совместно с граничными условиями, которые в теории упругости ставятся на границе среды.
Отметим, что граничные условия в линейной теории упругости ставятся на недеформированных границах.
(*)

СМЕЩЕНИЕ АТОМОВ В КРИСТАЛЛИЧЕСКОЙ РЕШЕТКЕ С ТОЧЕЧНЫМИ ДЕФЕКТАМИ.
ИЗМЕНЕНИЕ ОБЪЕМА.
Исходя из уравнения (*) и считая, что в рассматриваемой области объемные силы равными нулю, получим:
центральная симметрия:
Uϕ = Uθ = 0.

А. рассмотрим случай бесконечной среды
B = 0
R=∝
Константа A называется мощностью дефекта.

изменение объема изотропной среды, связанное с наличием дефекта
- если дефект внутри поверхности
- если дефект вне поверхности
дефект представляет собой δ-образную особенность.
относительное изменение объема кристалла:
точечный дефект в бесконечной изотропной среде вызывает только сдвиговое смещение.

Б. Рассмотрим случай конечного твердого тела радиуса R
закон Гука для радиальной составляющей напряжений
Введем постоянную Эшелби