Описанная и вписанная окружности

АРХИМЕД (287-212 ДО Н.Э.) – древнегреческий математик и механик.
Древние математики не владели понятиями математического анализа. Однако они умели вычислять длины окружности и некоторых спиралей
Вычисляя периметры правильных вписанных 2n -угольников, Архимед нашёл, что число π, участвующее в формуле длины окружности и площади круга:С=2 π r S= πR2, заключено между 3 10/71 и 31/7, т.е. 3,1408 <π <3,1429

Цели работы
Выявление связи между математикой, историей, информатикой, изобразительным искусством, алгеброй и геометрией
Выяснить, действительно ли число π равно 3,14…

Задачи исследования:
Нахождение дополнительной информации в ходе посещения в библиотеку
Заочное путешествие в историческую науку и в историю математики
Сравнивать результаты компьютерного эксперимента с вычислениями учёных древности

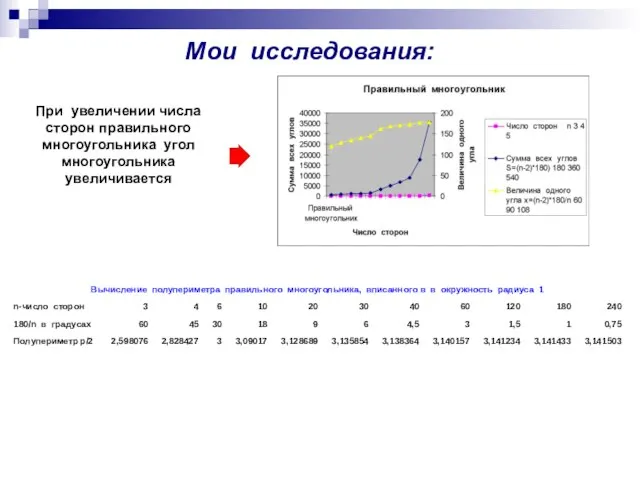
Мои исследования:
При увеличении числа сторон правильного многоугольника угол многоугольника увеличивается

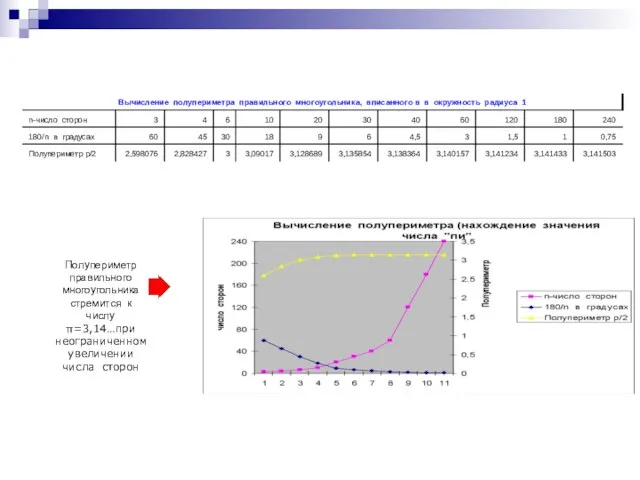
Полупериметр правильного многоугольника стремится к числу π=3,14…при неограниченном увеличении числа сторон

Без угла и без вершин
Нет начала, нет конца
Думаете, что «прямая»?
Нет! Ведь замкнута она
Длина окружности вычисляется по формуле С = 2πR
Окружность

Это круг
Кругом называется часть плоскости, ограниченная окружностью
Площадь круга вычисляется по формуле
S = πR2
Круг

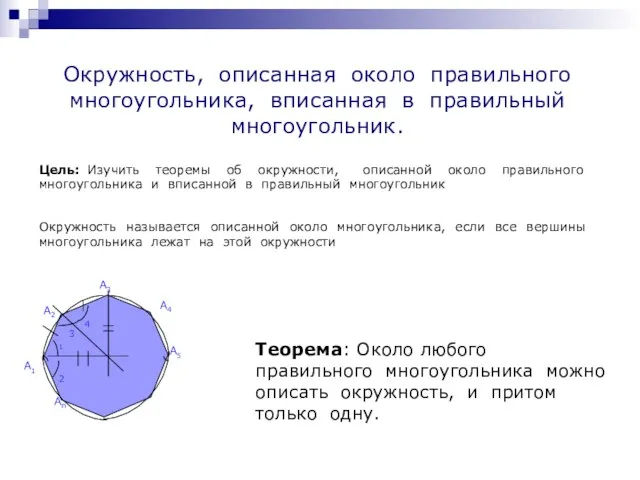
Окружность, описанная около правильного многоугольника, вписанная в правильный многоугольник.
Цель: Изучить теоремы об окружности, описанной около правильного многоугольника и вписанной в правильный многоугольник
Окружность называется описанной около многоугольника, если все вершины многоугольника лежат на этой окружности
Теорема: Около любого правильного многоугольника можно описать окружность, и притом только одну.

Окружность называется вписанной в многоугольник, если все стороны многоугольника касаются этой окружности
Теорема:
В любой правильный многоугольник можно вписать окружность, и притом только одну.

Предлагаем на размышление:
Задача1:
Докажите, что площадь S треугольника вычисляется по формуле:
S =½*P*r, где Р - периметр треугольника, к- радиус вписанной окружности.
Задача 2.
Решить задачу: Даны стороны треугольника АВС –а, в, с и площадь S. Выразить радиусы окружностей, описанной около треугольника и вписанной в него, через а, в, с и S

ВЫВОДЫ:
В ходе исследования мы узнали , что правильные многоугольники, окружность и круг встречаются и применяются в жизни.
В частности, мы узнали что при увеличении числа сторон правильного многоугольника угол многоугольника увеличивается. Полупериметр правильного многоугольника стремится к числу π = 3,14…при неограниченном увеличении числа сторон
Математика своими корнями уходит в далекое прошлое. Мы можем ответить на проблемные вопросы.