Содержание
- 2. Математическая статистика Математическая статистика - область науки, изучающая случайные явления, разрабатывающая математические методы систематизации, обработки и
- 3. Переменные Данные (data) представляют собой результаты наблюдений, испытаний, накапливаемые с целью последующего изучения и анализа. Переменная,
- 4. Определения Генеральная совокупность (population) - вся интересующая исследователя совокупность изучаемых объектов. Выборка, выборочная совокупность (sample) -
- 5. Измерение явлений Измерение (measurement) означает присвоение чисел характеристикам изучаемых объектов, явлений согласно некоторому правилу. Шкала (scale)
- 6. Типы данных Дискретные данные (discrete data) представляют собой отдельные значения признака, общее число которых конечно либо
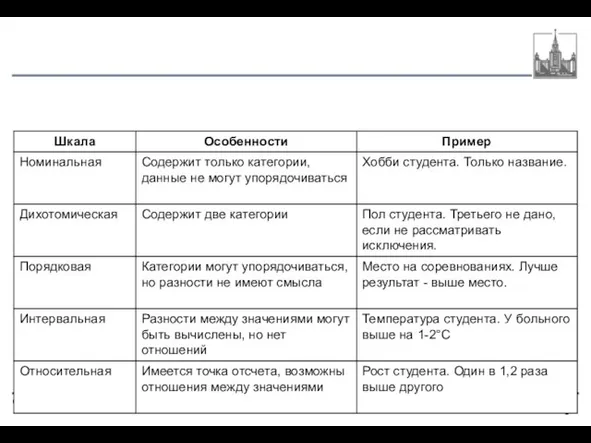
- 7. Измерительные шкалы (С. Стивенс) номинативная, или номинальная, или шкала наименований (в том числе дихотомическая) порядковая, или
- 9. 3.1. Измерение центральной тенденции Мода Медиана Среднее
- 10. Постановка задачи Измерение центральной тенденции (measure of central tendency) состоит в выборе одного числа, которое наилучшим
- 11. Мода Мода – наиболее часто встречающееся значение в выборке, наборе данных. Обозначается Мо. Выборка: 5,4 1,2
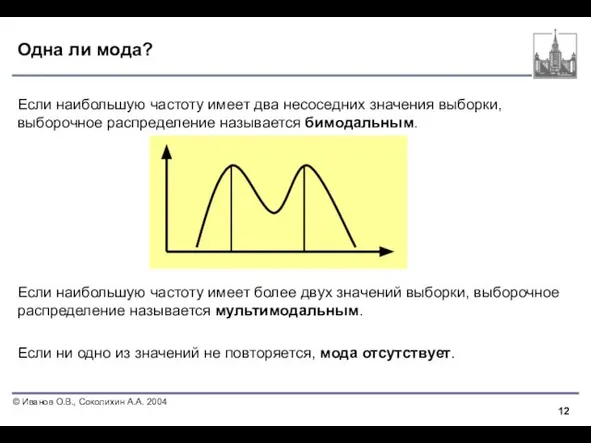
- 12. Одна ли мода? Если наибольшую частоту имеет два несоседних значения выборки, выборочное распределение называется бимодальным. Если
- 13. Свойства моды 1. Наличие одного или двух крайних значений, сильно отличающихся от остальных, не влияет на
- 14. Вариационный ряд Вариационный ряд - упорядоченные данные, расположенные в порядке возрастания значения признака, либо в порядке
- 15. Ранжирование Ранжирование означает присвоение числам рангов. Ранжирование данных производится после упорядочения. Ранги присваиваются от 1 до
- 16. Медиана Медиана есть значение серединного элемента для набора данных. Обозначается Me. Для нахождения медианы требуется составить
- 17. Пример вычисления медианы Для набора данных из семи чисел: 6 1 3 7 1 7 3
- 18. Свойства медианы 1. Сильно отличающиеся от остальных данных крайние значения не влияют на величину медианы. 2.
- 19. Среднее значение Выборочное среднее будем называть среднее арифметическое выборки, то есть сумму всех значений выборки, деленную
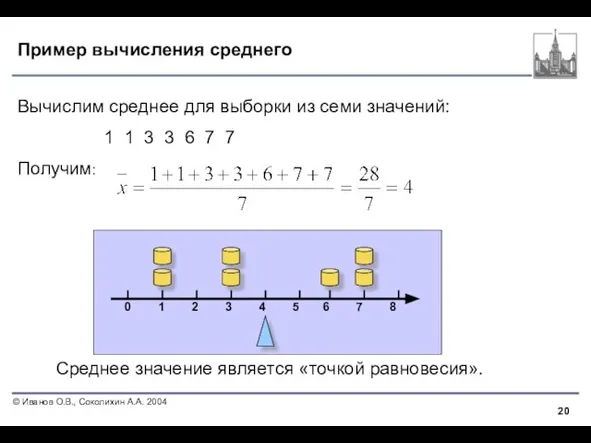
- 20. Пример вычисления среднего Среднее значение является «точкой равновесия». Вычислим среднее для выборки из семи значений: 1
- 21. Свойства среднего 1. Вычисляется только в числовых шкалах. 2. При ее вычислении необходимо использовать все данные.
- 22. Среднее для сгруппированных данных Среднее для сгруппированных данных вычисляется по формуле: где = сумма всех значений
- 23. Пример вычисления среднего Имеются результаты экзамена. Найти среднее значение. xi fi xi·fi 0 1 0 1
- 24. Среднее - еще не значит «лучшее» Пример. В деревне 50 жителей. Среди них 49 человек –
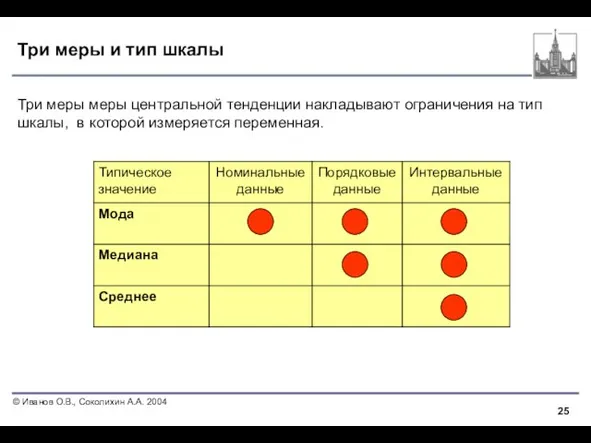
- 25. Три меры и тип шкалы Три меры меры центральной тенденции накладывают ограничения на тип шкалы, в
- 26. Среднее для дихотомической шкалы Среднее может также применяться и для переменной, измеренной в дихотомической шкале. Если
- 27. Какое типическое значение наилучшее? «Наилучшее значение» - это такое значение, что для случайно взятого элемента выборки
- 28. * 3.2. Измерение вариации Размах Дисперсия Стандартное отклонение
- 29. Постановка задачи Рассмотрим три вариационных ряда: а) 999, 1000, 1001 б) 900, 1000, 1100 в) 1,
- 30. Размах (Range) Размах – разность между наибольшим значением набора данных и наименьшим. Пример: Для набора данных
- 31. Подсчет дисперсии в таблице Дисперсию удобно рассчитывать при помощи таблицы. В первом столбце выборка. Второй и
- 32. Вторая формула для дисперсии Дисперсия вычисляет также по равносильной формуле: Считается, что эта формула более пригодна
- 33. Подсчет дисперсии в таблице Пример вычисления дисперсии по второй формуле. В таблице рассчитываются лишь квадраты значений.
- 34. Дисперсия для сгруппированных данных Дисперсия для сгруппированных данных вычисляется по формуле: Вычисления удобно проводить при помощи
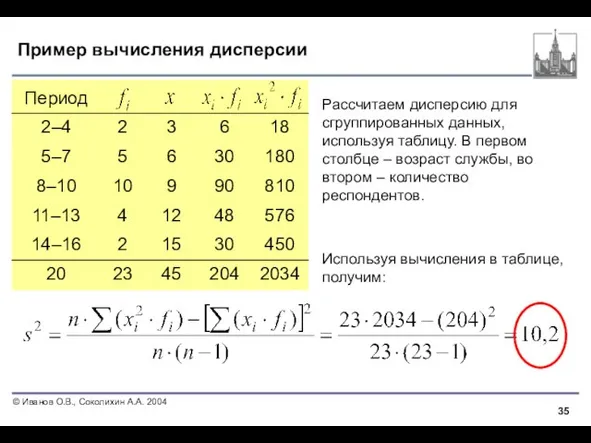
- 35. Пример вычисления дисперсии Рассчитаем дисперсию для сгруппированных данных, используя таблицу. В первом столбце – возраст службы,
- 36. Стандартное отклонение Стандартное отклонение вычисляется как корень из дисперсии: Стандартное отклонение имеет исключительную важность для описания
- 37. Интерпретация стандартного отклонения На интервале с границами содержится, по крайней мере, 3/4 всех данных (75%). На
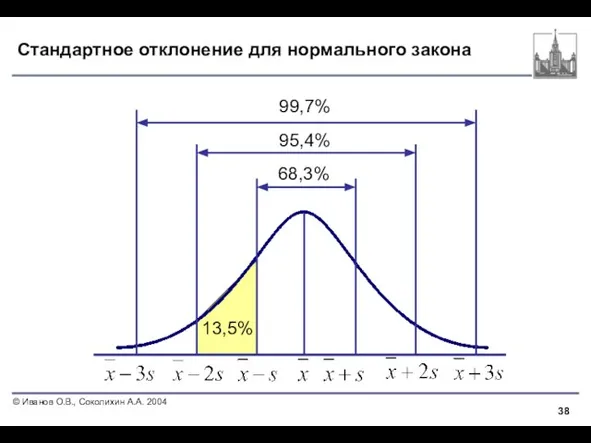
- 38. Стандартное отклонение для нормального закона 68,3% 95,4% 99,7% 13,5%
- 39. Коэффициент вариации Коэффициент вариации вычисляется как отношение стандартного отклонения к среднему: Коэффициент вариации полезен, если: 1.
- 40. Пример для коэффициента вариации Какие данные имеют большую вариацию: имеющие стандартное отклонение 20 при среднем 200
- 42. Скачать презентацию

































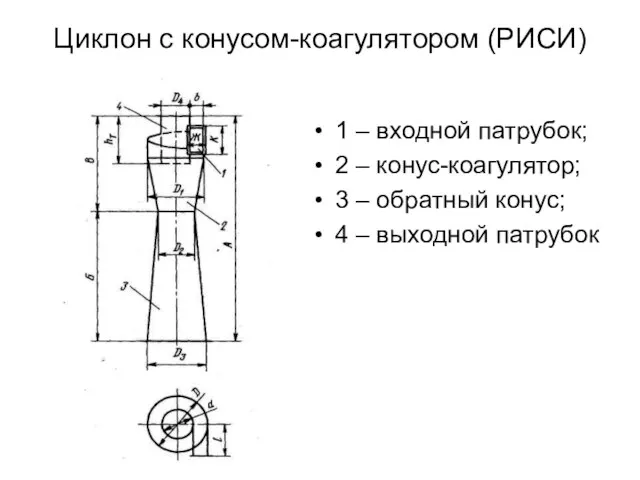 Циклон с конусом-коагулятором (РИСИ)
Циклон с конусом-коагулятором (РИСИ)  Маркетинговое исследование рынка молочной продукции по дисциплине маркетинг
Маркетинговое исследование рынка молочной продукции по дисциплине маркетинг Инновационные подходы к формированию индивидуальных программ реабилитации инвалидов.
Инновационные подходы к формированию индивидуальных программ реабилитации инвалидов. People’s Princess. The Truly Story About Lady Diana
People’s Princess. The Truly Story About Lady Diana Рисунки к 100 летию Г.А. Илизарова
Рисунки к 100 летию Г.А. Илизарова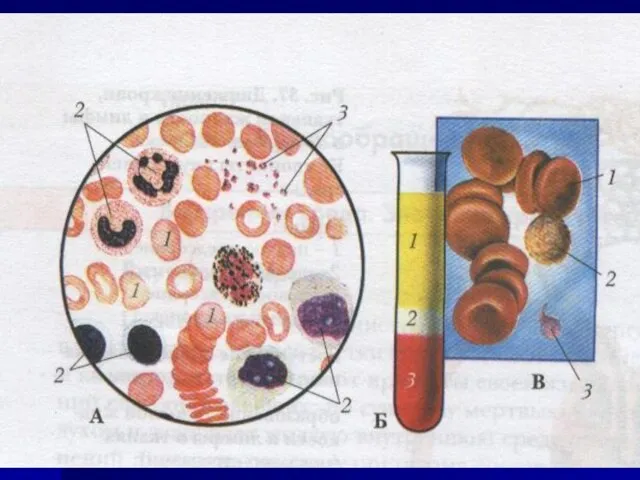 Строение сердца. Сердце – это жизнь
Строение сердца. Сердце – это жизнь Презентация на тему Характеристика биогеоценоза
Презентация на тему Характеристика биогеоценоза  Концептуальные и методологические аспекты управления финансами российских вузов
Концептуальные и методологические аспекты управления финансами российских вузов ACQUISITION OPPORTUNITIES IN RUSSIAN BRAKE
ACQUISITION OPPORTUNITIES IN RUSSIAN BRAKE  Проект БАРС. Требования к кандидатам
Проект БАРС. Требования к кандидатам Функции контроллера
Функции контроллера Памятник собакам
Памятник собакам General Pharmacology
General Pharmacology Личный кабинет педагога. Помощь в работе или дополнительная нагрузка
Личный кабинет педагога. Помощь в работе или дополнительная нагрузка Общая информация, логотип отеля
Общая информация, логотип отеля Ювенальная юстиция Австралии
Ювенальная юстиция Австралии Современный компьютер. Перспективы развития
Современный компьютер. Перспективы развития Русская школа генетики
Русская школа генетики Научная работа «Глушение скважин в условиях АНПД. Эффективность внедрения технологических растворов для ремонта скважин на осно
Научная работа «Глушение скважин в условиях АНПД. Эффективность внедрения технологических растворов для ремонта скважин на осно Поиск ключевого бизнес-партнёра. Система сопровождения и развития ключевых партнеров
Поиск ключевого бизнес-партнёра. Система сопровождения и развития ключевых партнеров Электрический ток
Электрический ток The Big Bang Social Theory!
The Big Bang Social Theory! Презентация на тему Гестозы
Презентация на тему Гестозы Afischa-1
Afischa-1 ОТКРЫТЫЙ ИНСТИТУТ ОХРАНЫ ТРУДА, ПРОМЫШЛЕННОЙБЕЗОПАСНОСТИ И ЭКОЛОГИИ
ОТКРЫТЫЙ ИНСТИТУТ ОХРАНЫ ТРУДА, ПРОМЫШЛЕННОЙБЕЗОПАСНОСТИ И ЭКОЛОГИИ 1.1. Каждый из 500 студентов посещают три спецкурса. Спецкурс только по математике, только по математике и физике, только по физике и а
1.1. Каждый из 500 студентов посещают три спецкурса. Спецкурс только по математике, только по математике и физике, только по физике и а Пермский государственный национальный исследовательский университетИтоги научно-исследовательской работы университета в 2011 го
Пермский государственный национальный исследовательский университетИтоги научно-исследовательской работы университета в 2011 го Война с Ганнибалом
Война с Ганнибалом