Определение:

Назвать функции, заданные формулами и соответствующие им графики.

Свойства функции:
область определения функции
область значений функции
четность функции
возрастание (убывает) функции
наибольшее и наименьшее значения функции
ограниченность снизу (сверху)

Определение:
Логарифмом положительного числа b по основанию а, где а>0, а≠1, называется показатель степени, в которую надо возвести а, чтобы получить b.

Записаны формулы, определите, какие из них записаны неверно:

Самостоятельная работа
Вычислите:
1 вариант.
2 вариант.

Проверка:
Ответы:1 вариант: -2;-1;0;1;2;3; нет.
Ответы:2 вариант: 2;1;0;-1;-2;-3; нет.

Итак, мы повторили необходимый материал.
С какими трудностями вы встретились при выполнении самостоятельной работы?

Вернемся к заданиям самостоятельной работы на повторение понятия логарифма.
Задание. Обозначьте изменяющуюся величину через x. При этом значение логарифма тоже будет изменяться. Обозначьте его через y и задайте формулой полученную зависимость y от x.
Итак, ребята, что у вас получилось?

Задаются ли этими формулами функции?...
Объясните, почему?
Посмотрите внимательно на правую часть формулы.
Подумайте, как бы вы назвали эту функцию?
и
Задаются ли этими формулами функции?...
Объясните, почему?
Посмотрите внимательно на правую часть формулы.
Подумайте, как бы вы назвали эту функцию?

Тема урока:

Тема урока:
«Логарифмическая функция, её свойства и график».

Цели урока.
Ввести понятие логарифмической функции, дать определение.
Изучить основные свойства логарифмической функции.
Сформировать умение выполнять построение графика логарифмической функции.

Постройте графики функций по вариантам используя результаты самостоятельной работы
I вариант II вариант

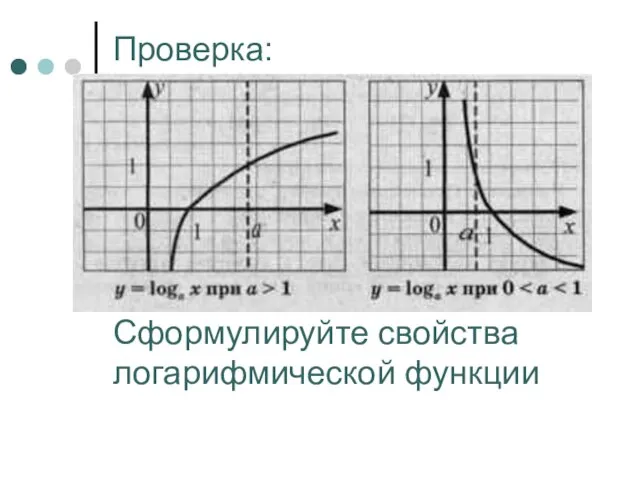
Проверка:
Сформулируйте свойства логарифмической функции

Свойства логарифмической функции.
область определения - множество всех положительных чисел (х>0).
область значений - множество всех действительных чисел
( - ∞; +∞).
непрерывна на всей области определения.
функция возрастает на всей области определения, если а>1.
функция убывает на всей области определения, если 0< а>1.
точка пересечения графика функции с осью Ох (1,0).
наибольшего и наименьшего значения функции не существует.
положение точки а относительно1, и значения функции при х=а

Закрепление нового материала.
Стр 243, № 69
Объясните, как при сравнении значений логарифмов, вы будете использовать свойство возрастания (убывания) функции.

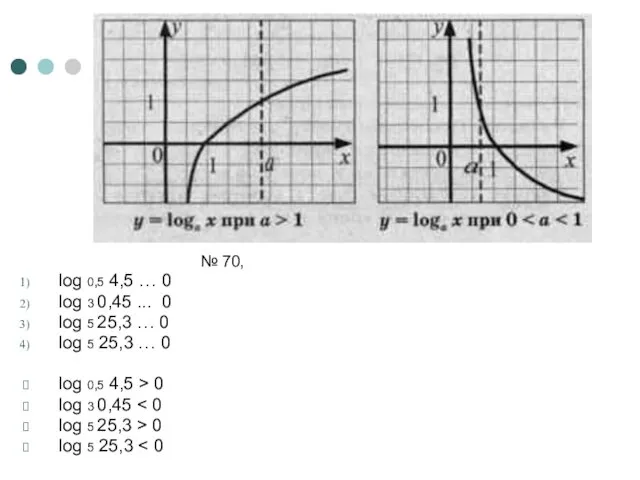
№ 70,
log 0,5 4,5 … 0
log 3 0,45 ... 0
log 5 25,3 … 0
log 5 25,3 … 0
log 0,5 4,5 > 0
log 3 0,45 < 0
log 5 25,3 > 0
log 5 25,3 < 0

Задание.
Постройте график функции

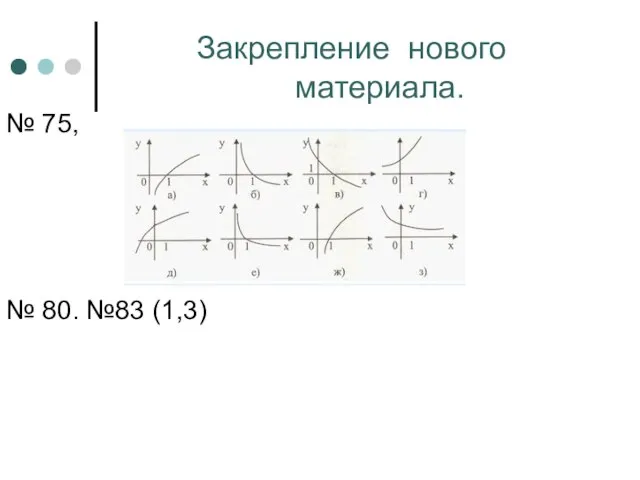
Закрепление нового материала.
№ 75,
№ 80. №83 (1,3)

В математике встречаются немного экзотические графики. Одним из них является логарифмическая спираль.

ПРЕЗЕНТАЦИЯ НА ТЕМУ
«ЛОГАРИФМИЧЕСКАЯ СПИРАЛЬ»
Презентацию выполнил
ученик 10 «А»
Максим Щетков

В математике встречаются немного экзотические графики. Одним из них является логарифмическая спираль. Спираль имеет бесконечное множество витков и при раскручивании, и при скручивании. Логарифмическую спираль называют еще равноугольной спиралью. Это ее название отражает тот факт, что в любой точке логарифмической спирали угол между касательной к ней и радиус-вектором сохраняет постоянное значение.

Уравнение логарифмической спирали
Логарифмическая спираль описывается уравнением r=aф, где r – расстояние от точки, вокруг которой закручивается спираль (ее называют полюсом), до произвольной точки на спирали, ф – угол поворота относительно полюса, а – постоянная.
Спираль называется логарифмической, т.к. логарифм расстояния (logar) возрастает пропорционально углу поворота ф.

Свойства логарифмической спирали
Произвольный луч, выходящий из полюса спирали, пересекает любой виток спирали под одним и тем же углом.
Логарифмическая спираль не изменяет своей природы при многих преобразованиях, к которым чувствительны другие кривые. Сжать или растянуть эту спираль – то же самое, что повернуть ее на определенный угол.

Свойства логарифмической спирали
Если вращать спираль вокруг полюса по часовой стрелке, то можно наблюдать кажущееся растяжение спирали.

Логарифмическая спираль в природе
Один из наиболее распространенных пауков, эпейра, сплетая паутину, закручивает нити вокруг центра по логарифмической спирали.
Хищные птицы кружат над добычей по логарифмической спирали. Дело в том, что они лучше видят, если смотрят не прямо на добычу, а чуть в сторону.

Живые существа обычно растут, сохраняя общее очертание своей формы. При этом они растут чаще всего во всех направлениях - взрослое существо и выше и толще детеныша. Но раковины морских животных могут расти лишь в одном направлении. Чтобы не слишком вытягиваться в длину, им приходится скручиваться, причем каждый следующий виток подобен предыдущему. А такой рост может совершаться лишь по логарифмической спирали или ее некоторым пространственным аналогам. Поэтому раковины многих моллюсков, улиток, а также рога таких млекопитающих, как архары, закручены по логарифмической спирали.

Можно сказать, что эта спираль является математическим символом соотношения форм роста. Великий немецкий поэт Иоганн Вольфганг Гете считал ее даже математическим символом жизни и духовного развития. Очертания, выраженные логарифмической спиралью, имеют не только раковины, в подсолнухе семечки расположены по дугам, также близким к логарифмической спирали.