ОПТИМИЗАЦИЯ НЕСТАЦИОНАРНЫХ ЗАДАЧ КОМБИНАТОРНОГО ТИПА С ПОМОЩЬЮ ГЕНЕТИЧЕСКИХ АЛГОРИТМОВ Д.И.Батищев, Е.А.Неймарк, Н.В. Старостин 200
Содержание
- 2. Задача нестационарной дискретной оптимизации
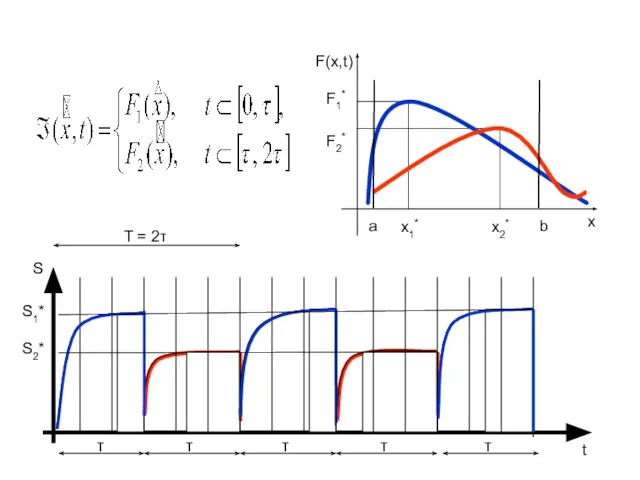
- 3. Вид целевой функции
- 4. F1* F2* x1* x2* F(x,t) x S1* S2* t a b S
- 5. Стационарная задача об одномерном ранце
- 6. Нестационарная задача об одномерном ранце
- 7. Стационарная задача коммивояжера
- 8. Нестационарная задача коммивояжера
- 9. Методы решения нестационарных задач методы увеличения генетического разнообразия при изменении среды [2,10], методы постоянного поддержания генетического
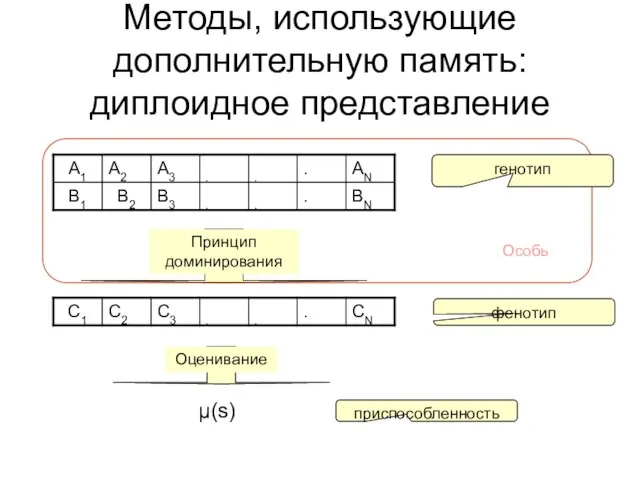
- 10. Методы, использующие дополнительную память: диплоидное представление μ(s) генотип фенотип приспособленность
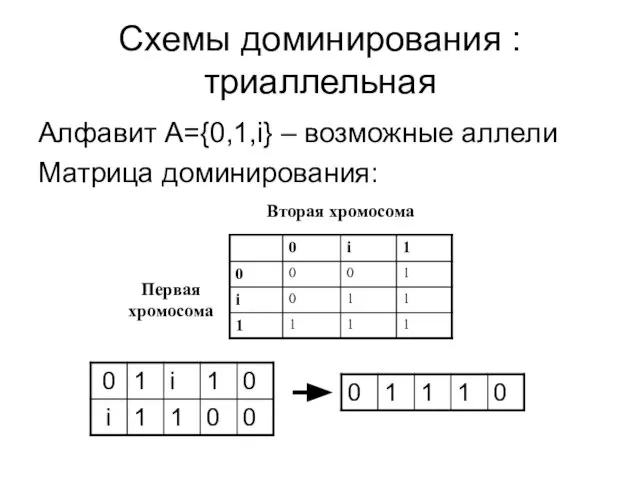
- 11. Схемы доминирования : триаллельная Алфавит А={0,1,i} – возможные аллели Матрица доминирования:
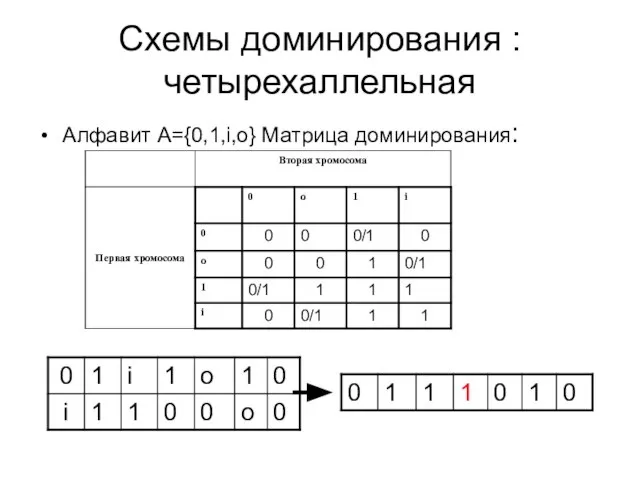
- 12. Схемы доминирования : четырехаллельная Алфавит А={0,1,i,o} Матрица доминирования:
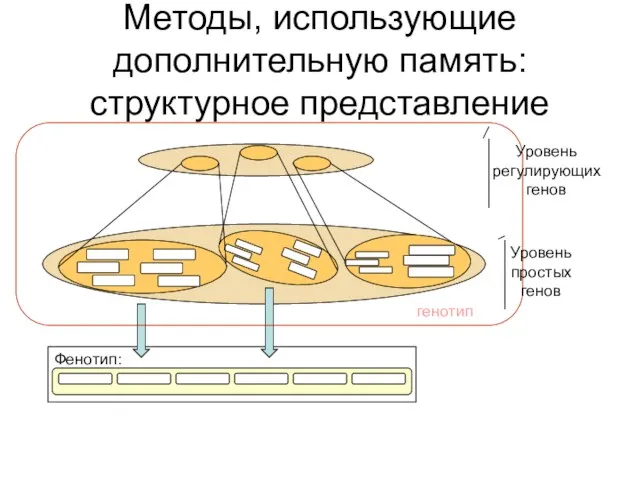
- 13. Методы, использующие дополнительную память: структурное представление генотип Уровень регулирующих генов Уровень простых генов
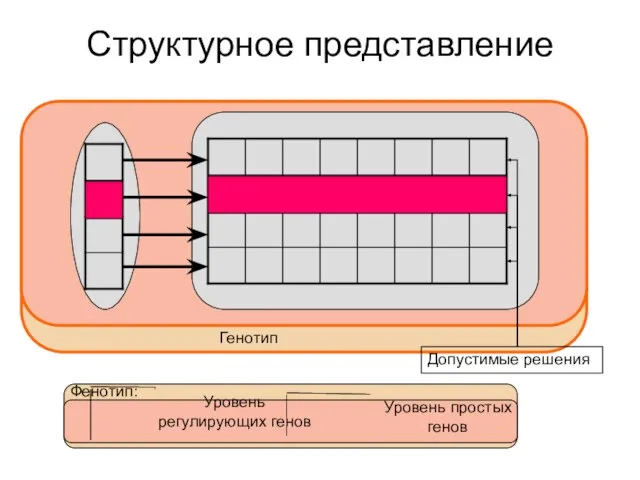
- 14. Структурное представление Допустимые решения Уровень регулирующих генов Уровень простых генов
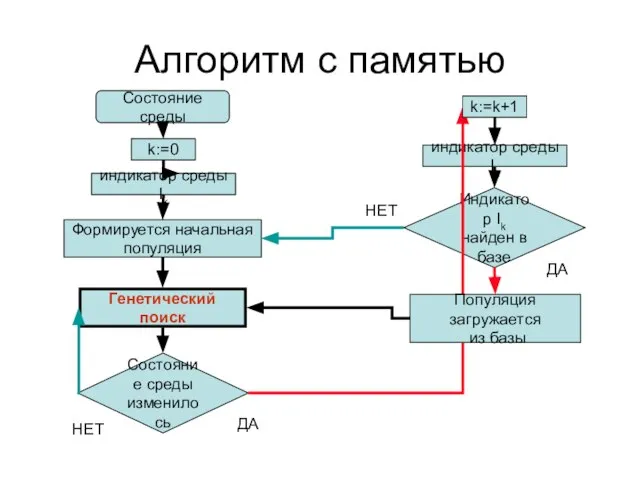
- 15. Алгоритм с памятью Формируется начальная популяция Состояние среды изменилось Генетический поиск Состояние среды индикатор среды Ik
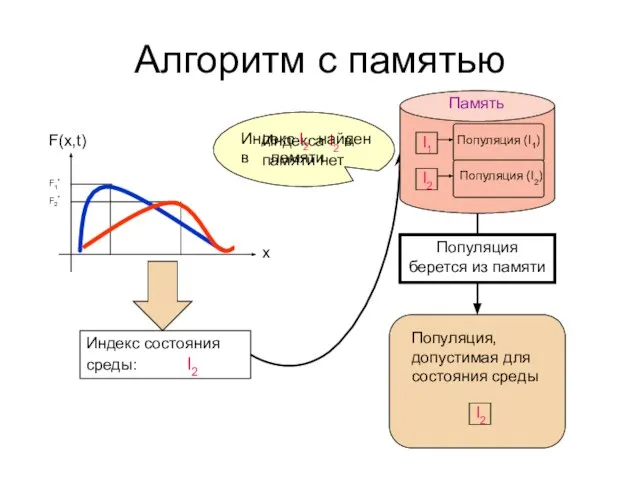
- 16. Алгоритм с памятью F(x,t) x Индекс состояния среды: I2 Память Индекса I2 в памяти нет Индекс
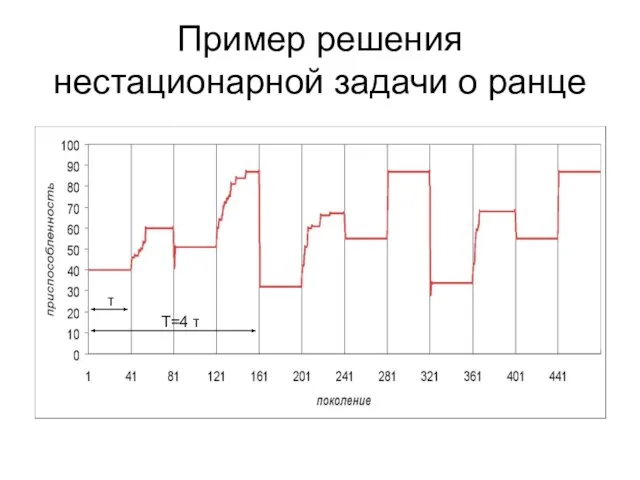
- 17. Пример решения нестационарной задачи о ранце
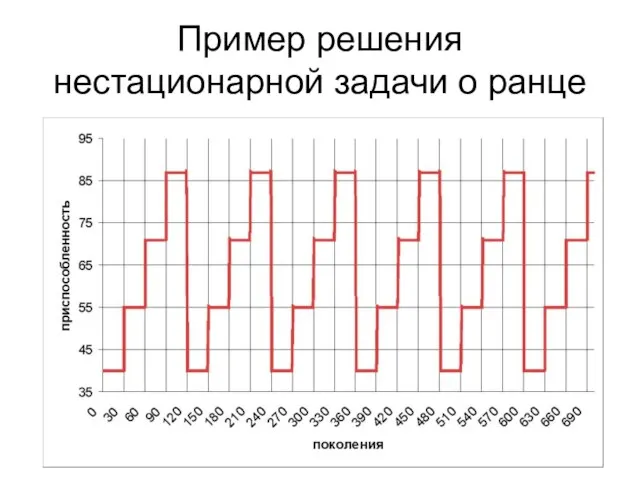
- 18. Пример решения нестационарной задачи о ранце
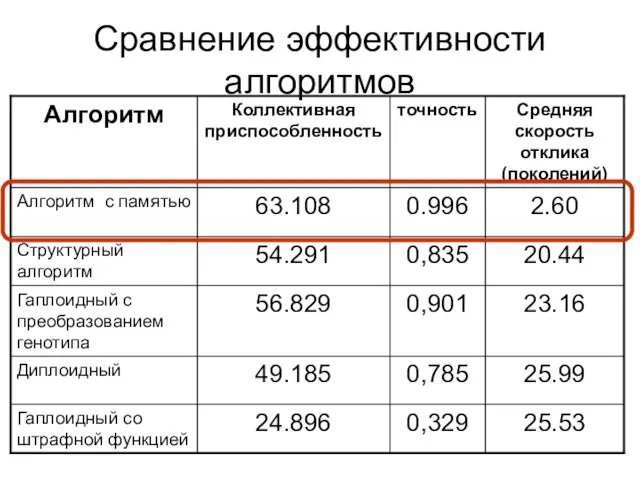
- 19. Меры эффективности алгоритмов для нестационарных задач Точность [11] Средняя коллективная приспособленность [7] Средняя скорость отклика –
- 20. Сравнение эффективности алгоритмов
- 22. Скачать презентацию






![Методы решения нестационарных задач методы увеличения генетического разнообразия при изменении среды [2,10],](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/444396/slide-8.jpg)
![Меры эффективности алгоритмов для нестационарных задач Точность [11] Средняя коллективная приспособленность [7]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/444396/slide-18.jpg)
 Творческое объединение лего-мастерская Шелезяка. Робототехника
Творческое объединение лего-мастерская Шелезяка. Робототехника Cовременные окрашивание волос
Cовременные окрашивание волос Veselaya_azbuka_10_09_16
Veselaya_azbuka_10_09_16 Bunker - лидеры рынка
Bunker - лидеры рынка Тестування Потреба відображає
Тестування Потреба відображає Что такое театр?
Что такое театр? Начало петровской эпохи
Начало петровской эпохи  Культурное наследие кочевников
Культурное наследие кочевников City (Город)
City (Город) Менеджер по рекламе
Менеджер по рекламе ДЕЛОПРОИЗВОДСТВЕНННЫЕ МАТЕРИАЛЫ
ДЕЛОПРОИЗВОДСТВЕНННЫЕ МАТЕРИАЛЫ Браузер- окно в мир Internet
Браузер- окно в мир Internet Золотое кольцо России
Золотое кольцо России методы когнитивного исследования (презентация Анны Киселевой)
методы когнитивного исследования (презентация Анны Киселевой) Идеи новогоднего макияжа
Идеи новогоднего макияжа Лекция Тема: «Зарубежный опыт организации государственной службы»
Лекция Тема: «Зарубежный опыт организации государственной службы» Главная улица Москвы Если вы пройдете через Александровский сад и повернете налево,
Главная улица Москвы Если вы пройдете через Александровский сад и повернете налево, Как вести себя в опасных ситуациях
Как вести себя в опасных ситуациях Презентация на тему Первые люди
Презентация на тему Первые люди  Холодная война
Холодная война ПРОСТРАНСТВО ДОМА В РУССКОМ ЯЗЫКОВОМ СОЗНАНИИ
ПРОСТРАНСТВО ДОМА В РУССКОМ ЯЗЫКОВОМ СОЗНАНИИ Ниточный дизайн
Ниточный дизайн Формирование соединений при сварке давлением. (Лекция 2)
Формирование соединений при сварке давлением. (Лекция 2) Медициналық ортадағы кикілжің
Медициналық ортадағы кикілжің Латунь в машиностроении
Латунь в машиностроении Сотовый телефон. Вреден ли он для здоровья 4 класс
Сотовый телефон. Вреден ли он для здоровья 4 класс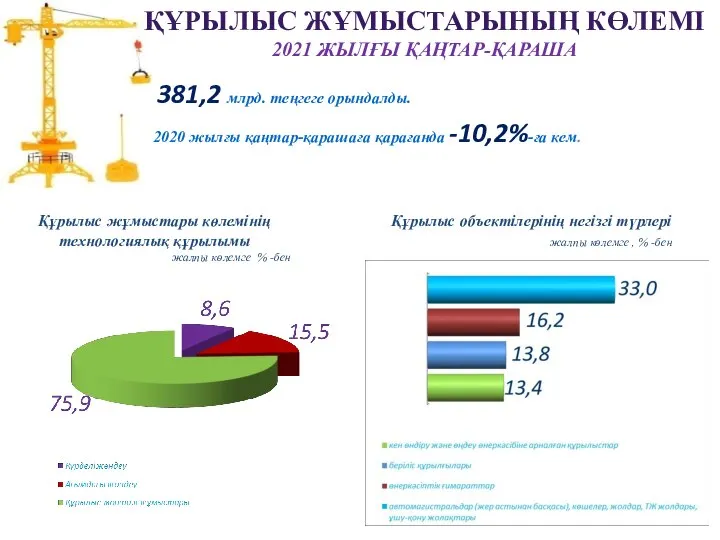 Подряд_KZ_11.21
Подряд_KZ_11.21 Африканская саванна
Африканская саванна