Оптимизация химико-технологических процессов

ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИ ХТП
Оптимизация ХТП – это достижение наилучших результатов функционирования ХТП (Химико-Технологического Процесса)в смысле заданного критерия оптимальности (целевой функции) при заданных условиях.
Корректное решение задачи оптимизации ХТП возможна при выполнении следующих условий:
выбран или сформулирован критерий оптимальности, представляющий собой количественную оценку качества функционирования ХТП
используемый при решении задачи оптимизации функционирующий критерий оптимальности является единственным и количественным
имеются в распоряжении ресурсы оптимизации – оптимизирующие или управляющие параметры процесса (ХТП)
функционирующий критерий оптимальности является чувствительным к изменению оптимизирующих параметров ХТП
разработана и реализована на компьютере адекватная модель процесса
выбран и реализован на компьютере алгоритм оптимизации ХТП

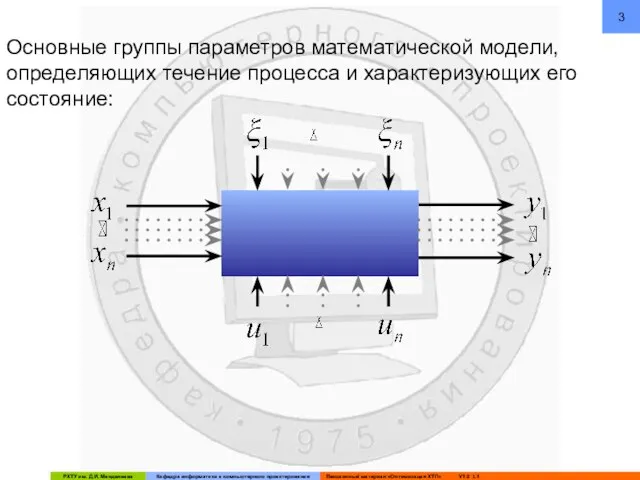
Основные группы параметров математической модели, определяющих течение процесса и характеризующих его состояние:

- Входные параметры (влияющие на состояние процесса, но на которые нельзя воздействовать)
- Управляющие(оптимизирующие) параметры – ресурсы оптимизации (влияющие на состояние процесса, на них можно воздействовать)
- Возмущающие параметры (не учитываются в случае детерминированных процессов)
- Выходные параметры (характеризуют состояние процесса).

ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИ ХТП
Математическая модель детерминированного процесса,
которая может быть реализована на компьютере
с применением alg ММ:
Критерий оптимальности детерминированного процесса:

Решение задачи оптимизации – определение наименьшего (в частном случае, min )или наибольшего (в частном случае, max) величины R с применением alg ОПТ.
Поскольку выходные параметры зависят от параметров
и , критерий оптимальности R при решении
задачи оптимизации считается функцией только входных и управляющих параметров процесса:
ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИ ХТП

ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИ ХТП
Таким образом, задача оптимизации может быть решена с применением компьютера только тогда, когда известен вид зависимостей:
или адекватная математическая модель, позволяющая при различных входных и управляющих параметрах процесса определять его выходные параметры.

Однако так как на входные параметры нельзя воздействовать,
они не могут быть оптимизирующими или управляющими параметрами.
Задача оптимизации решается с целью определения оптимальных значений оптимизирующих или управляющих параметров ,
при которых критерий оптимальности (целевая функция) R принимает наибольшее (в частном случае – максимальное) или наименьшее (в частном случае – минимальное) значение.
Корректное решение задачи оптимизации возможно только в диапазоне входных , управляющих и выходных
параметров, в которых обеспечивается адекватность модели процесса.
В этом случае задача формулируется как задача на поиск экстремума функции многих переменных
в области допустимых значений оптимизирующих (управляющих) параметров .
ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИ ХТП

Если в дальнейшем принять, что , то формулировка задачи оптимизации имеет вид и, в общем случае, является задачей на экстремум функции многих переменных (экстремальной задачей):
Таким образом, для решения задачи оптимизации требуется определить такие значения оптимизирующих или управляющих параметров из области их допустимых значений , при которых R принимает максимальное или минимальное значение.
ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИ ХТП

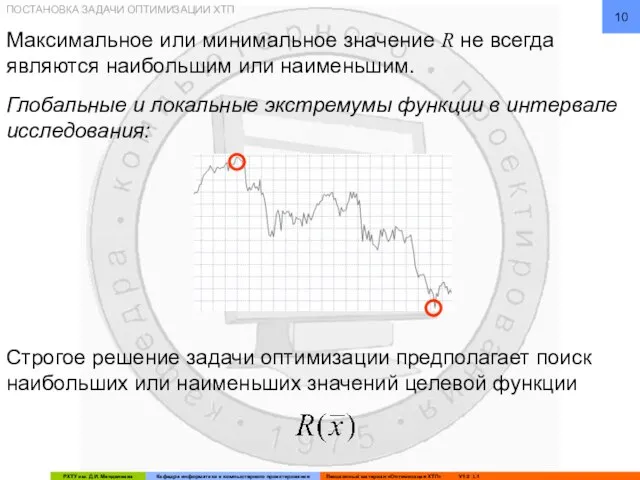
Максимальное или минимальное значение R не всегда являются наибольшим или наименьшим.
Глобальные и локальные экстремумы функции в интервале исследования:
ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИ ХТП
Строгое решение задачи оптимизации предполагает поиск наибольших или наименьших значений целевой функции

ИССЛЕДОВАНИЕ ЭКСТРЕМУМА ФУНКЦИЙ МЕТОДОМ КЛАССИЧЕСКОГО МАТЕМАТИЧЕСКОГО АНАЛИЗА
Методы исследования функций классического анализа могут применяться в случае, если известен вид зависимости
При этом возможно аналитическое определение производных оптимизируемой функции R, используемых для формирования необходимых и достаточных условий существования экстремума.

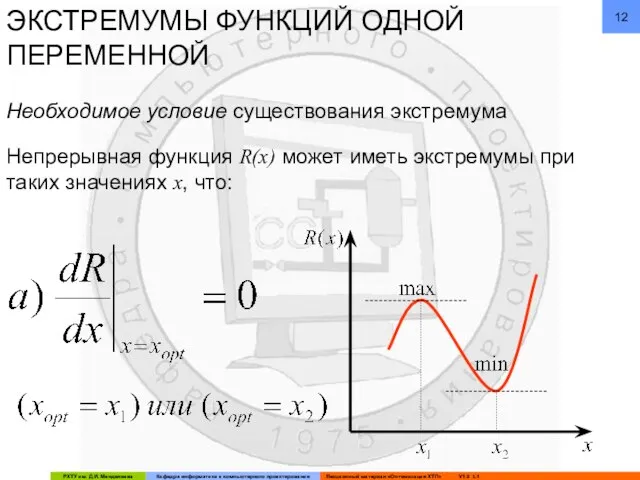
ЭКСТРЕМУМЫ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
Непрерывная функция R(x) может иметь экстремумы при таких значениях x, что:
Необходимое условие существования экстремума

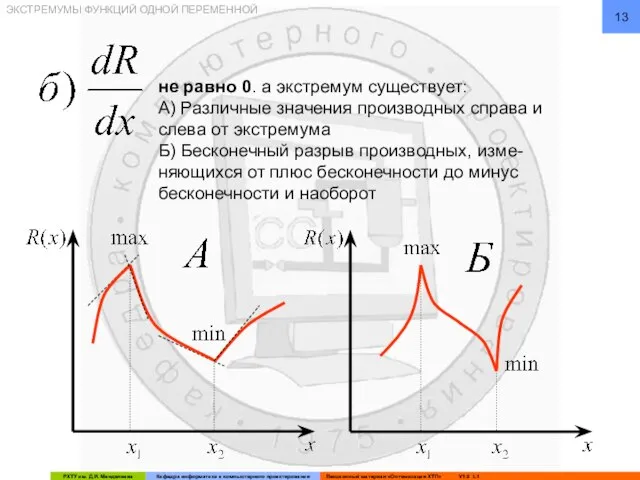
не равно 0. а экстремум существует:
А) Различные значения производных справа и
слева от экстремума
Б) Бесконечный разрыв производных, изме-
няющихся от плюс бесконечности до минус
бесконечности и наоборот
ЭКСТРЕМУМЫ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ

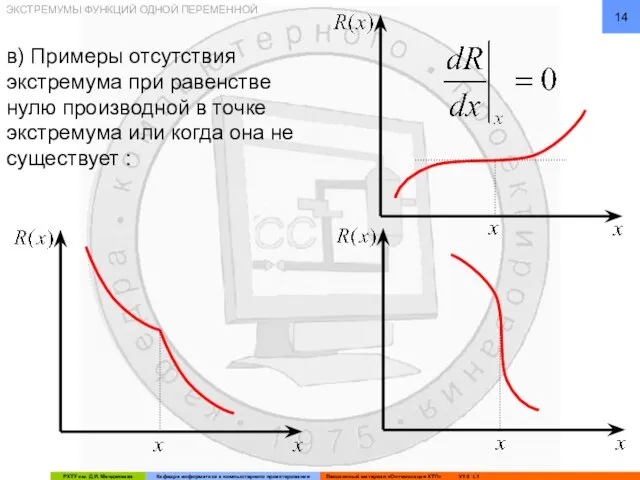
в) Примеры отсутствия экстремума при равенстве нулю производной в точке
экстремума или когда она не существует :
ЭКСТРЕМУМЫ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ

Для подтверждения наличия экстремумов в определенных точках необходимо проводить дополнительные исследования:
Сравнение значений функции справа и слева от предполагаемого экстремума
Сравнение знаков производных функции справа и слева от предполагаемого экстремума
Исследование знаков производных высших порядков
ЭКСТРЕМУМЫ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ

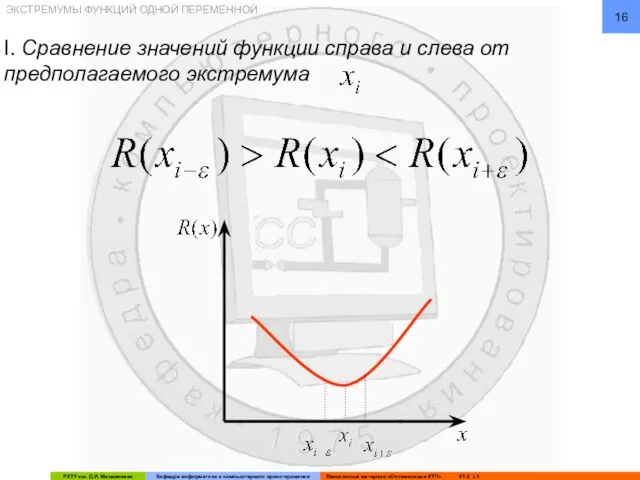
ЭКСТРЕМУМЫ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
I. Сравнение значений функции справа и слева от предполагаемого экстремума

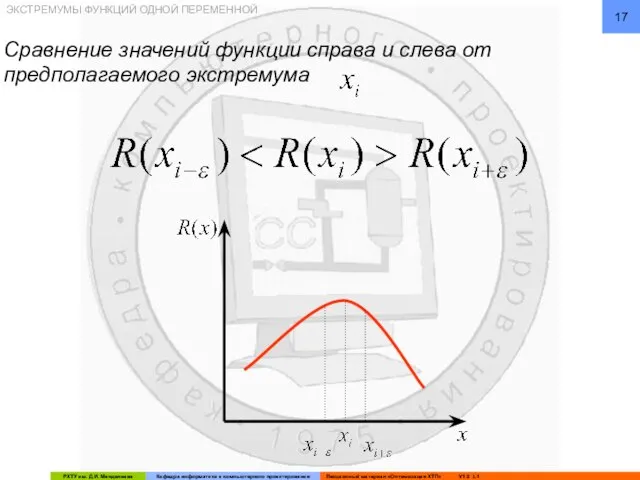
ЭКСТРЕМУМЫ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
Сравнение значений функции справа и слева от предполагаемого экстремума

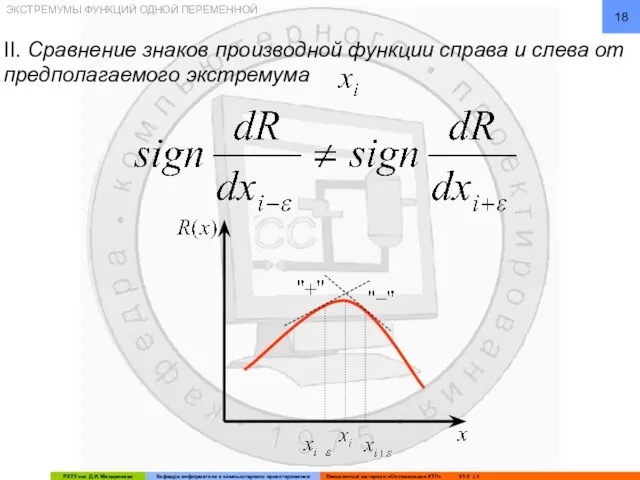
ЭКСТРЕМУМЫ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
II. Сравнение знаков производной функции справа и слева от предполагаемого экстремума

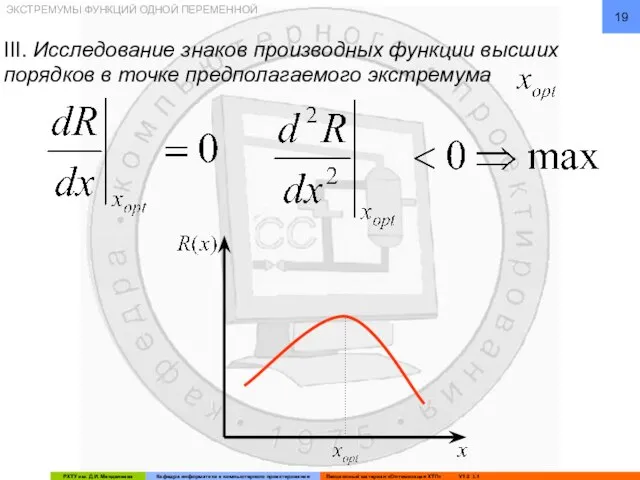
ЭКСТРЕМУМЫ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
III. Исследование знаков производных функции высших порядков в точке предполагаемого экстремума

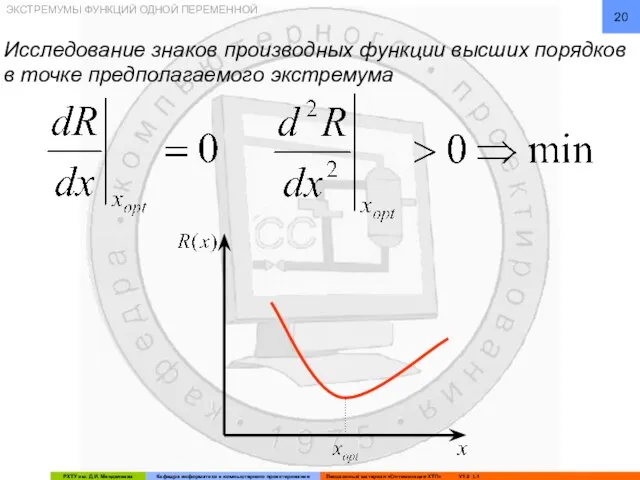
ЭКСТРЕМУМЫ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
Исследование знаков производных функции высших порядков в точке предполагаемого экстремума

ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
Функция многих переменных имеет в точке
максимум (минимум), если существует такая окрестность этой точки, взятая на области определения функции, что для всех точек этой окрестности справедливо следующее неравенство:
или

ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
Необходимым условием существования экстремума функции многих переменных в точке является равенство нулю частных производных первого порядка по всем переменным:

ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
Равнозначным условием является условие равенства нулю полного дифференциала дифференцируемой функции
в точке экстремума
Поскольку

Разложив функцию в окрестности точки в ряд Тейлора по степеням :
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
Достаточные условия существования экстремума функции многих переменных

ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
с учётом необходимого условия существования экстремума:

ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
Если выражение
сохраняет один и тот же знак для любых приращений
то экстремум функции в точке существует.

Приращение целевой функции в окрестности экстремума определяется

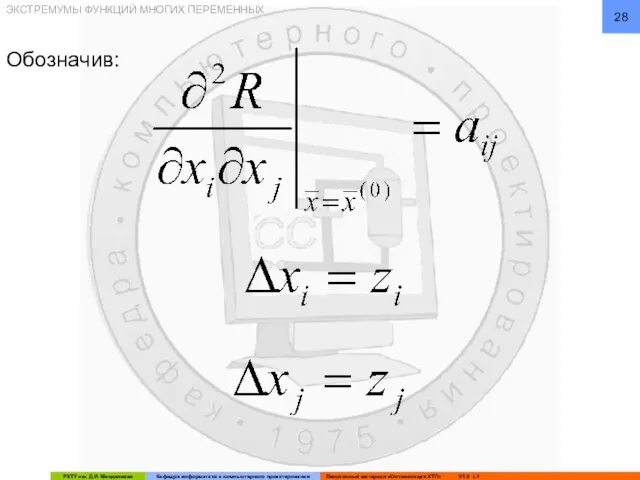
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
Обозначив:

ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
получаем выражение вида:
где - квадратичная форма.

ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
Условие положительной определённости квадратичной формы (достаточных условий существования минимума):
при любых значениях и
а в точке и

ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
Квадратичная форма будет положительно определённой, если все определители, составленные из элементов положительны (условия Сильвестра):

ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
ДОСТАТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМА ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ
Все определители Сильвестра положительны (положительно определенная квадратичная форма): R( )= min
Определители Сильвестра нечетного порядка отрицательны, а четного порядка - положительны (отрицательно определенная квадратичная форма):
R( )= max
Иная последовательность чередования знаков определителей Сильвестра:седловая точка=экстремума нет

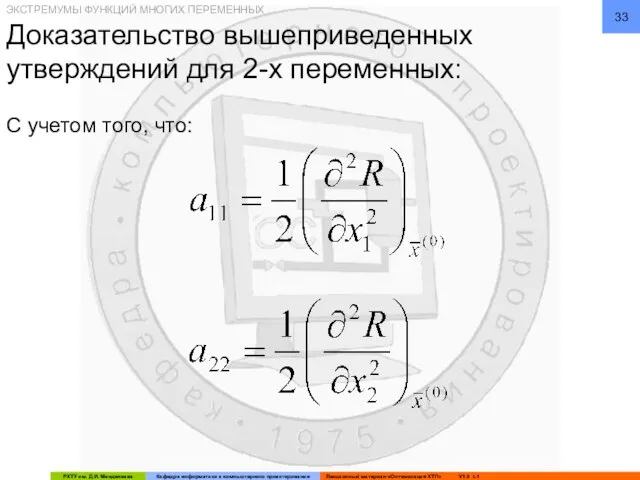
Доказательство вышеприведенных утверждений для 2-х переменных:
С учетом того, что:
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ

и:
Квадратичная форма второго порядка записывается:
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ

Преобразование последнего выражения приводит к соотношению:
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ

Отсюда следует:
Квадратичная форма будет положительно определенной, если:
и:
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ

Или в соответствии с условиями Сильвестра:
и:
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ

Квадратичная форма будет отрицательно определенной, если:
и:
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ

Знак неравенства в последнем случае будет отрицателен, когда числитель выражения после его приведения к общему знаменателю будет положителен, так как является отрицательным числом .
Из этого следует, что в соответствии с условиями Сильвестра (учитывая, что ), квадратичная форма будет отрицательно определенной в случае следующей системы чередования знаков определителей:
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ

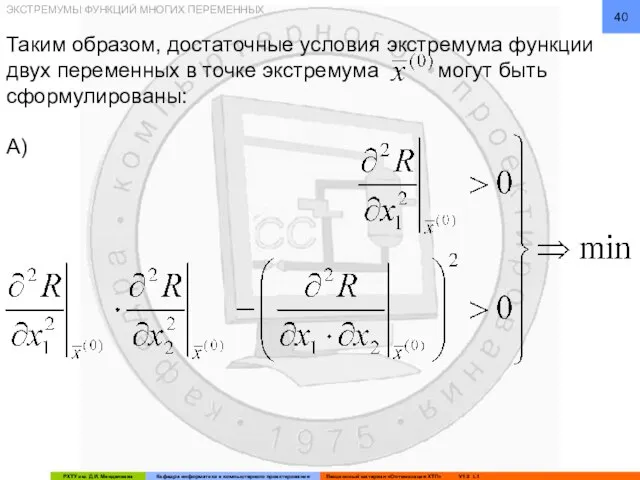
Таким образом, достаточные условия экстремума функции двух переменных в точке экстремума могут быть сформулированы:
А)
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ

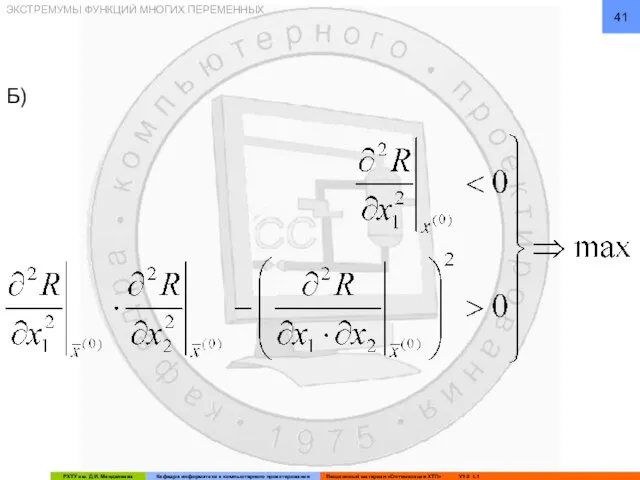
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
Б)

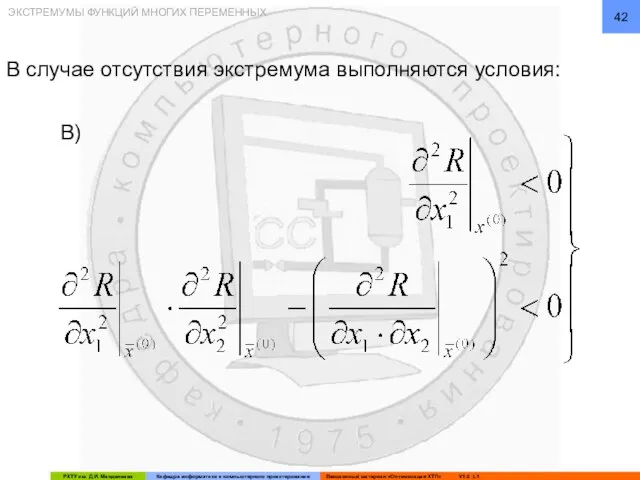
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
В случае отсутствия экстремума выполняются условия:
В)

ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
Следует отметить, что аналитическая проверка достаточных условий экстремума функции многих переменных не всегда возможна.
В таких случаях прибегают к вычислительным экспериментам на компьютере, либо вывод о существовании экстремума может вытекать из физического смысла решаемой задачи.

ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ
Рассмотрим химическую реакцию с целевым продуктом P, проходящую по схеме:

ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ
Скорость реакции по целевому продукту выражается по закону действующих масс:
Необходимо определить температуру T проведения реакции, при которой:

ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ
Необходимое условие экстремума:

ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ

ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ

ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ
В состоянии равновесия скорость реакции W равна 0:

ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ

ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ
Получаем связь равновесной и оптимальной температур проведения реакции:

ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ
откуда:

ОПТИМИЗАЦИЯ РАВНОВЕСНЫХ ЭКЗОТЕРМИЧЕСКИХ РЕАКЦИЙ
После логарифмирования получаем: