Основы логики и логические основы компьютера

Содержание
Формы мышления
Алгебра высказываний
Логические выражения и таблицы истинности
Логические функции
Логические законы и правила преобразования лог.выражений
Логические основы устройства компьютера

1. Формы мышления
Логика – это наука о формах и способах мышления.
Основные формы мышления:
Понятие
Высказывание
Умозаключение
содержание

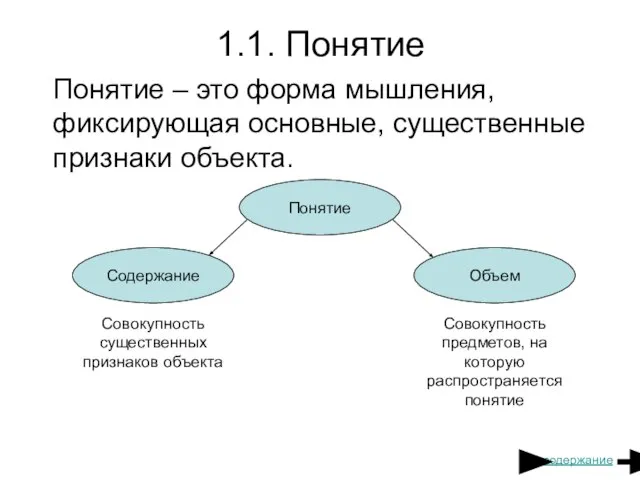
1.1. Понятие
Понятие – это форма мышления, фиксирующая основные, существенные признаки объекта.
Понятие
Содержание
Объем
Совокупность существенных признаков объекта
Совокупность предметов, на которую распространяется понятие
содержание

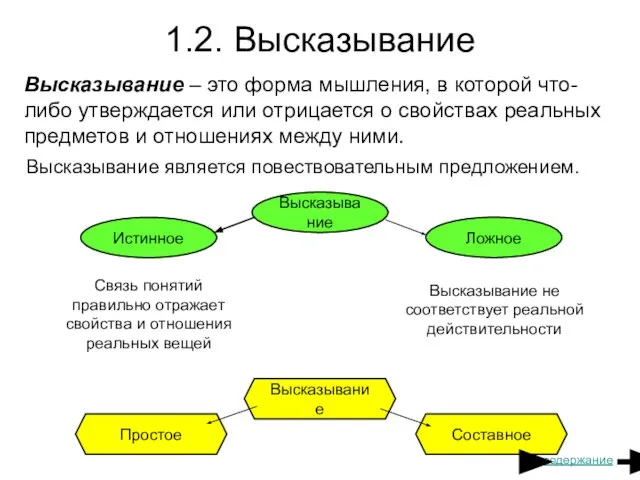
1.2. Высказывание
Высказывание – это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними.
Высказывание является повествовательным предложением.
Высказывание
Истинное
Ложное
Связь понятий правильно отражает свойства и отношения реальных вещей
Высказывание не соответствует реальной действительности
Высказывание
Простое
Составное
содержание

1.3. Умозаключение
Умозаключение – это форма мышления, с помощью которой из одного или нескольких суждений (посылок) может быть получено новое суждение (заключение).
Посылки – только истинные суждения.
содержание

2. Алгебра высказываний
Алгебра высказываний служит для определения истинности или ложности составных высказываний.
Высказывания обозначаются именами логических переменных, которые могут принимать лишь два значения: «истина» (1) и «ложь» (0).
содержание

Логические операции
2.1. Логическое умножение (конъюнкция)
2.2. Логическое сложение (дизъюнкция)
2.3. Логическое отрицание (инверсия)
содержание

2.1. Логическое умножение (конъюнкция)
Объединение двух (или нескольких) высказываний в одно с помощью союза «и».
Составное высказывание истинно только тогда, когда истины оба простых высказывания.
Соответствует союзу И
Обозначение &, ^
В языках программирования and;
Таблица истинности
содержание

2.2. Логическое сложение
(дизъюнкция)
Объединение двух (или нескольких) высказываний в одно с помощью союза «или».
Составное высказывание истинно только тогда, когда истинно хотя бы одно из двух простых высказывания.
Соответствует союзу ИЛИ
Обозначение V
В языках программирования or
Таблица истинности
содержание

2.3. Логическое отрицание
(инверсия)
Присоединение частицы «не» к высказыванию.
Инверсия делает истинное высказывание ложным и, наоборот.
Соответствует союзу НЕ
Обозначение Ā
В языках программирования not
Таблица истинности
содержание

3. Логические выражения и таблицы истинности
Логическое выражение – формула, в которую входят логические переменные Логическое выражение – формула, в которую входят логические переменные и знаки логических операций.
Пример:
Для логического выражения можно построить таблицу истинности, которая определяет его истинность или ложность при всех возможных комбинациях исходных значений простых высказываний.
содержание

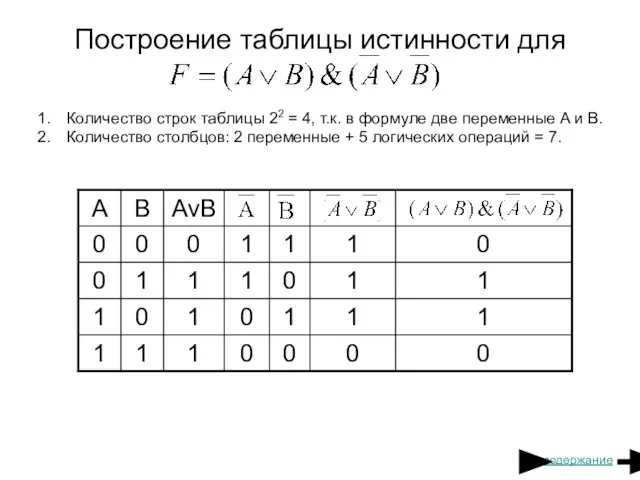
Построение таблицы истинности
Определить количество строк в таблице по формуле 2n, где n – количество логических переменных.
Определить количество столбцов таблицы: количество логических переменных + количество логических операций.
Построить таблицу истинности, обозначить столбцы, внести всевозможные наборы исходных данных логических переменных.
Заполнить таблицу истинности, выполняя базовые логические операции в необходимой последовательности.
содержание

Построение таблицы истинности для
Количество строк таблицы 22 = 4, т.к. в формуле две переменные A и B.
Количество столбцов: 2 переменные + 5 логических операций = 7.
содержание

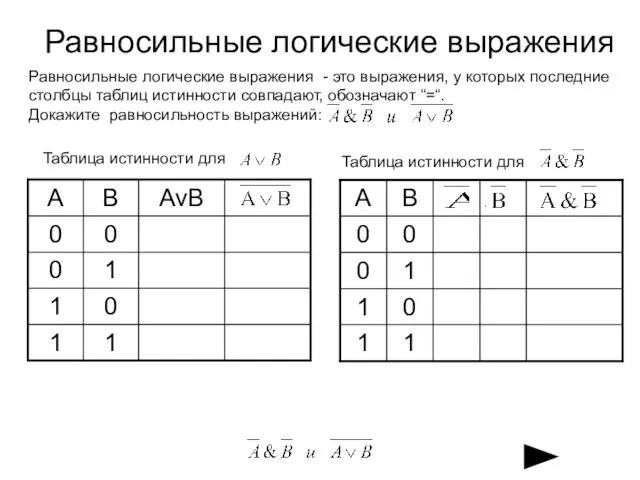
Равносильные логические выражения
Равносильные логические выражения - это выражения, у которых последние столбцы таблиц истинности совпадают, обозначают “=“.
Докажите равносильность выражений:
Таблица истинности для
Таблица истинности для

4. Логические функции
Любое составное высказывание можно рассматривать как логическую функцию F(X1, X2, …, Xn),
где X1, X2, …, Xn – простые высказывания.
Функция и аргументы могут принимать только два различных значения: «истина» (1) и «ложь» (0).
содержание

Таблицы истинности логических функций двух аргументов
содержание

Логическое следование (импликация)
Соответствует обороту Если…, то…
Обозначение А→В
В языках программирования if … then …
Импликация образуется соединением двух высказываний в одно с помощью оборота речи «если…, то…».
Импликация ложна только тогда, когда из истинного первого высказывания(предпосылки) следует ложный вывод (второе высказывание).
Таблица истинности
содержание

Все логические функции путем логических преобразований можно свести к трем базовым:
Логическому умножению
Логическому сложению
Логическому отрицанию
Методом сравнения таблиц истинности докажите:
Таблица истинности для A→B
Таблица истинности для

Логическое равенство
(эквивалентность)
Эквивалентность образуется соединением двух высказываний в одно с помощью оборота речи «… тогда и только тогда, когда …».
Составное высказывание, образованное с помощью логической операции эквивалентности истинно тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны.
Таблица истинности
Соответствует обороту тогда и только тогда, когда …
Обозначение А≡В, А~B
содержание

5. Логические законы и правила преобразования логических выражений
Закон тождества.
Всякое высказывание тождественно самому себе.
А=А
Закон непротиворечия.
Высказывание не может быть одновременно истинным и ложным.
Закон исключенного третьего.
Высказывание может быть либо истинным, либо ложным, третьего не дано.
Закон двойного отрицания.
Если дважды отрицать некоторое высказывание, то получим исходное высказывание.
содержание

Логические законы и правила преобразования логических выражений
Законы де Моргана.
Закон коммутативности.
A & B = B & A
A v B = B v A
Закон ассоциативности.
(A & B) & C = A & (B & C)
(A v B) v C = A v (B v C)
Закон дистрибутивности.
(A & B) v (A & C) = A & (B v C)
(A v B) & (A v C) = A v (B & C)
содержание

Решение логических задач
внимательно изучите условие;
выделить простые высказывания и обозначить их латинскими буквами;
записать условие задачи на языке алгебры логики;
составить конечную формулу, для этого объединить логическим умножением формулы каждого утверждения, приравнять произведение единице;
упростить формулу, проанализировать результат или составить таблицу истинности, найти по таблице значения переменных, для которых результат равен 1, проанализировать результат.
содержание

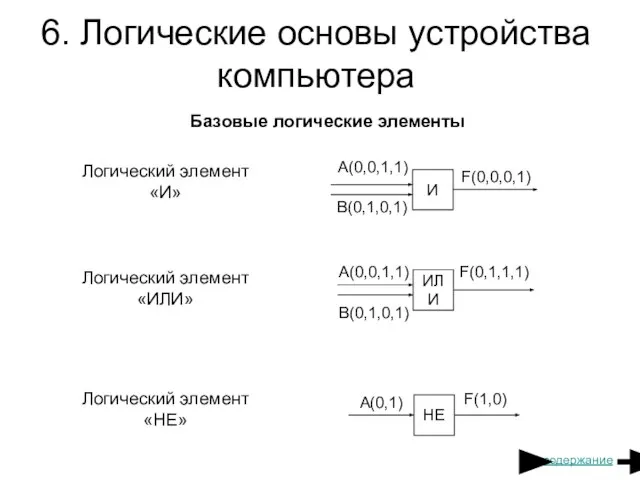
6. Логические основы устройства компьютера
Базовые логические элементы
Логический элемент
«И»
Логический элемент
«ИЛИ»
Логический элемент
«НЕ»
содержание

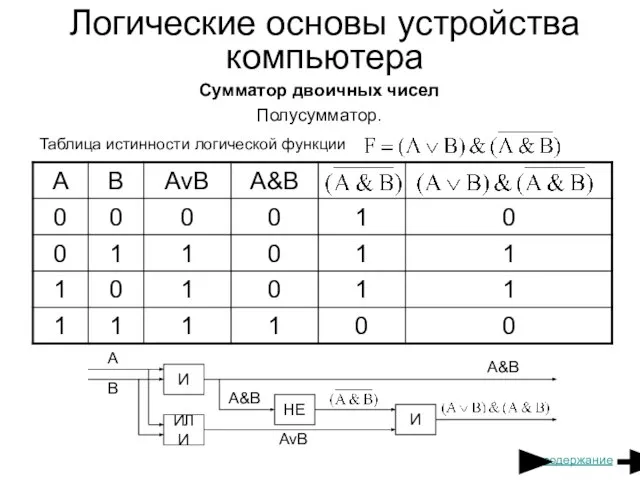
Сумматор двоичных чисел
Полусумматор.
A, B – слагаемые
P – перенос
S – сумма
P = A & B
Логические основы устройства компьютера
содержание

Логические основы устройства компьютера
Сумматор двоичных чисел
Полусумматор.
Таблица истинности логической функции
содержание

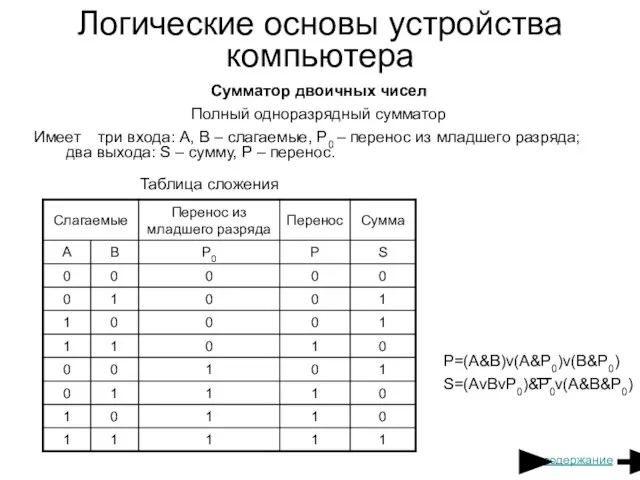
Логические основы устройства компьютера
Сумматор двоичных чисел
Полный одноразрядный сумматор
Имеет три входа: A, B – слагаемые, P0 – перенос из младшего разряда;
два выхода: S – сумму, P – перенос.
Таблица сложения
содержание