Основы логики. Логические основы компьютера

Логика (др.-греч. λογική — «наука о рассуждении», «искусство рассуждения» от λόγος — «речь», «рассуждение», «мысль») — наука о формах, методах и законах интеллектуальной познавательной деятельности, формализуемых с помощью логического языка.
Логика изучает мышление как средство познания объективного мира. Законы логики отражают в сознании человека свойства, связи и отношения объектов окружающего мира.

Идеи и аппарат логики используется в кибернетике, вычислительной технике и электротехнике (построение компьютеров основано на законах математической логики).
В основе логических схем и устройств ПК лежит специальный математический аппарат, использующий законы логики. Математическая логика изучает вопросы применения математических методов для решения логических задач и построения логических схем. Знание логики необходимо при разработке алгоритмов и программ, так как в большинстве языков программирования есть логические операции.

Алгебра логики – это раздел математики, возникший в XIX веке благодаря усилиям английского математика Дж. Буля. Поначалу булева алгебра не имела никакого практического значения. Однако уже в XX веке ее положения нашли применение в описании функционирования и разработке различных электронных схем. Законы и аппарат алгебры логики стал использоваться при проектировании различных частей компьютеров (память, процессор).

Алгебра логики – математический аппарат, с помощью которого записывают, упрощают, вычисляют и преобразовывают логические высказывания.
Высказывание – это повествовательное предложение, о котором можно сказать, что оно или истинно или ложно.
Высказывание может принимать только одно из двух логических значений: истина (1) или ложь (0).

Высказывание считается простым, если никакую его часть нельзя рассматривать как отдельное высказывание.
Примеры:
Земля - планета Солнечной системы (истинное)
Рим — столица Франции (ложное)

Сложное высказывание – высказывание, которое состоит из нескольких простых.
Сложное высказывание получается путем объединения простых высказываний логическими связками — НЕ, И, ИЛИ.
Пример:
На улице светит солнце или на улице пасмурная погода.

В алгебре логики, как и в обычной алгебре, вводится ряд операций. Логические связки И, ИЛИ и НЕ заменяются логическими операциями: конъюнкцией, дизъюнкцией и инверсией. Это основные логические операции, при помощи которых можно записать любую логическую функцию.

Инверсия (отрицание). Соответствует частице «не», означает «неверно». Обозначается черточкой над именем переменной или знаком ¬ перед переменной. Инверсия логической переменной истинна, если сама переменная ложна, и, наоборот, инверсия ложна, если переменная истинна.
Таблица истинности:

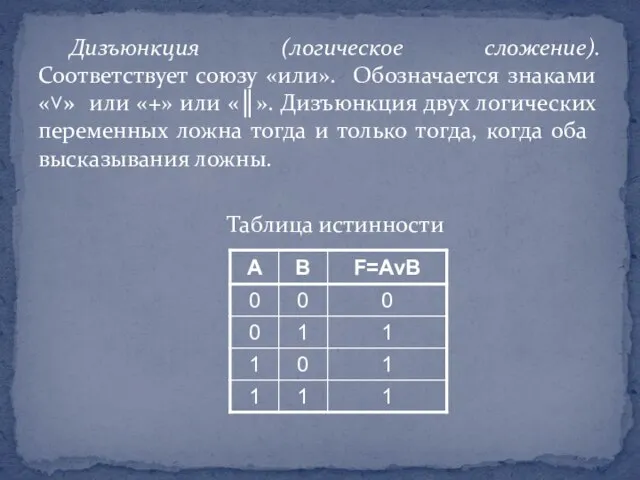
Дизъюнкция (логическое сложение). Соответствует союзу «или». Обозначается знаками «˅» или «+» или «║». Дизъюнкция двух логических переменных ложна тогда и только тогда, когда оба высказывания ложны.
Таблица истинности

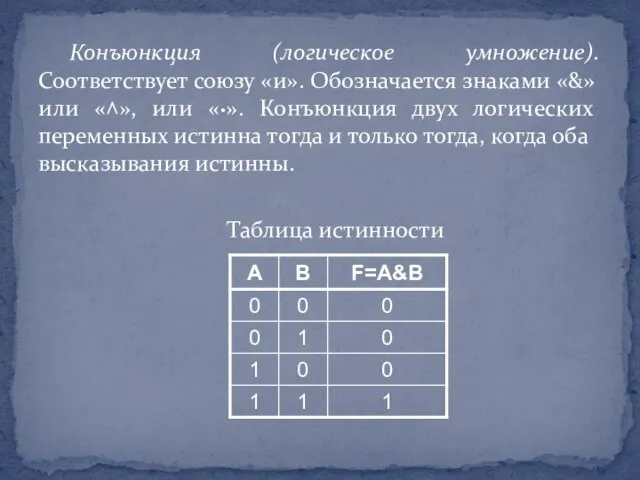
Конъюнкция (логическое умножение). Соответствует союзу «и». Обозначается знаками «&» или «˄», или «·». Конъюнкция двух логических переменных истинна тогда и только тогда, когда оба высказывания истинны.
Таблица истинности

Импликация (логическое следование). Связывает два простых логических выражения, из которых первое является условием (А), а второе (В) – следствием из этого условия. Результатом импликации является ложь только тогда, когда условие А истинно, а следствие В ложно. Обозначается символами «→» или «=>» и выражается словами «если…, то».
Таблица истинности

Эквиваленция (равнозначность). Определяет результат сравнения двух простых логических выражений А и В. Результатом эквиваленции является новое логическое выражение, которое будет истинным тогда и только тогда, когда оба исходных выражения одновременно истинны или ложны. Обозначается символами «=», «↔», «<=>».
Таблица истинности

Логическая переменная – переменная, которая может принимать только 2 значения – 0 и 1.
Логическое выражение – запись или устное утверждение, в которое, наряду с постоянными, обязательно входят переменные величины (объекты).
В зависимости от значений этих переменных логическое выражение может принимать одно из двух возможных значений: истина (логическая 1) или ложь (логический 0).

Операции в логическом выражении выполняются слева направо с учетом скобок в следующем порядке:
инверсия;
конъюнкция;
дизъюнкция;
импликация и эквивалентность.

Равносильности формул логики высказываний часто называют законами логики. Законы логики отражают наиболее важные закономерно­сти логического мышления.
В алгебре высказываний законы логики записываются в виде формул, которые позволяют проводить эквивалентные преобразования логических выражений в соответствие с законами логики.
Знание законов логики позволяет проверять правильность рассуждений и доказательств. Нарушения этих законов приводят к логическим ошибкам и вытекающим из них противоречиям.

Закон тождества. Всякое высказывание тождественно самому себе: А=А.
Этот закон сформулирован древнегреческим философом Аристотелем. Закон тождества утверждает, что мысль, заключенная в некотором высказывании, остается неизменной на протяжении всего рассуждения, в котором это высказывание фигурирует.
Закон непротиворечия. Высказывание не может быть одновременно истинным и ложным. Если высказывание А — истинно, то его отрицание Ᾱ должно быть ложным. Следовательно, логическое произведение высказывания и его отрицания должно быть ложно: А˄Ᾱ=0.

Закон исключенного третьего. Высказывание может быть либо истинным, либо ложным, третьего не дано.
Закон двойного отрицания. Если дважды отрицать неко­торое высказывание, то в результате мы получим исходное высказывание.
Законы идемпотентности. В алгебре логики нет показателей степеней и коэффициентов. Конъюнкция одинаковых «сомножителей» равносильна одному из них: А˄А=А.
Правило коммутативности. Можно менять местами логические переменные при операциях конъюнкции и дизъюнкции.
A&B=B&A
A˅B=B˅A

Логические элементы — это электронные устройства, которые преобразуют проходящие через них двоичные электрические сигналы по определенному закону.
Логические элементы имеют один или несколько входов, на которые подаются электрические сигналы, обозначаемые условно 0, если отсутствует электрический сигнал, и 1, если имеется электрический сигнал.
Также логические элементы имеют один выход, с которого снимается преобразованный электрический сигнал.
Было доказано, что все электронные схемы компьютера могут быть реализованы с помощью трёх базовых логических элементов И, ИЛИ, НЕ.

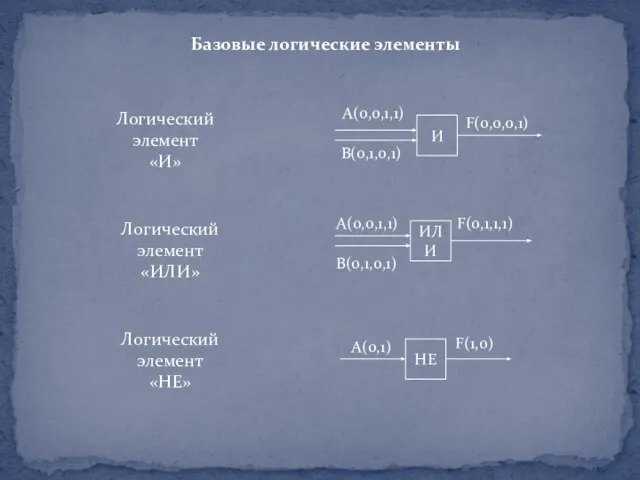
Базовые логические элементы
Логический элемент
«И»
Логический элемент
«ИЛИ»
Логический элемент
«НЕ»

Обработка любой информации на компьютере сводится к выполнению процессором различных арифметических и логических операций. Для этого в состав процессора входит так называемое арифметико-логическое устройство (АЛУ). Оно состоит из ряда устройств, построенных на рассмотренных выше логических элементах. Важнейшими из таких устройств являются триггеры, полусумматоры, сумматоры, шифраторы, дешифраторы, счетчики, регистры.

Сумматор – это электронная логическая схема, выполняющая суммирование двоичных чисел поразрядным сложением. Сумматор является центральным узлом арифметико-логического устройства процессора.
Сумматор выполняет сложение многозначных двоичных чисел. Он представляет собой последовательное соединение одноразрядных двоичных сумматоров, каждый из которых осуществляет сложение в одном разряде. Если при этом возникает переполнение разряда, то перенос суммируется с содержимым старшего соседнего разряда.

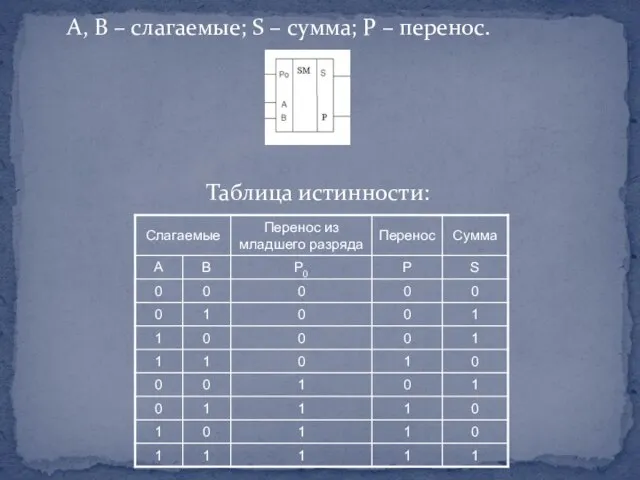
А, B – слагаемые; S – сумма; P – перенос.
Таблица истинности:

Триггер - электронная схема, применяемая для хранения значения одноразрядного двоичного кода.
Воздействуя на входы триггера, его переводят в одно из двух возможных состояний (0 или 1). С поступлением сигналов на входы триггера в зависимости от его состояния либо происходит переключение, либо исходное состояние сохраняется. При отсутствии входных сигналов триггер сохраняет свое состояние сколь угодно долго.