Основы реляционной алгебры

Появление теоретико-множественных моделей в системах баз данных было предопределено настоятельной потребностью пользователей в переходе от работы с элементами данных, как это делается в графовых моделях, к работе с некоторыми макрообъектами. Основной моделью в этом классе является реляционная модель данных.
Теоретической основой этой модели стала теория отношений, основу которой заложили два логика — американец Чарльз Содерс Пирс (1839-1914) и немец Эрнст Шредер (1841-1902).
Американский математик Эдгар Франк Кодд в 1970 году впервые сформулировал основные понятия и ограничения реляционной модели, ограничив набор операций в ней семью основными и одной дополнительной операцией. Предложения Кодда были настолько эффективны для систем баз данных, что за эту модель он был удостоен престижной премии Тьюринга в области теоретических основ вычислительной техники.

Основной структурой данных в модели является отношение, именно поэтому модель получила название реляционной (от английского relation — отношение).

Домен – это общее множество значений, из которых берутся конкретные значения определенного атрибута некоторого отношения (D)
Кортеж соответствует экземпляру записи
Степень (n – арность отношения)– количество атрибутов
Кардинальное число (кардинальность отношения) – количество кортежей содержащихся в отношении
Набор атрибутов, однозначно определяющий каждый объект, называют ключом.

Для таблицы должны выполняться следующие правила:
таблица имеет имя, отличное от имен других таблиц;
каждая клетка таблицы содержит только атомарное значение;
каждый столбец таблицы имеет уникальное имя;
данные для столбца берутся из одного множества значений (домен);
порядок следования столбцов не имеет значения;
таблица не имеет повторяющихся строк;
строки не имеют имен;
порядок следования строк не имеет значения.

Если атрибуты принимают значения из одного и того же домена, то они называются Q-сравпимыми, где Q множество допустимых операций сравнения, заданных для данного домена.
Например, если домен содержит числовые данные , то для него допустимы все операции сравнения, тогда Q = {=, <>,>=,<=,<,>}. Однако и для доменов, содержащих символьные данные, могут быть заданы не только операции сравнения по равенству и неравенству значений. Если для данного домена задано лексикографическое упорядочение, то он имеет также полный спектр операций сравнения.
Схемы двух отношений называются эквивалентными, если они имеют одинаковую степень и возможно такое упорядочение имен атрибутов в схемах, что на одинаковых местах будут находиться сравнимые атрибуты, то есть атрибуты, принимающие значения из одного домена.

В отличие от теоретико-графовых моделей в реляционной модели связи между отношениями поддерживаются неявным образом.
В каждой связи одно отношение может выступать как основное, а другое отношение выступает в роли подчиненного. Это означает, что один кортеж основного отношения может быть связан с несколькими кортежами подчиненного отношения. Для поддержки этих связей оба отношения должны содержать наборы атрибутов, по которым они связаны. В основном отношении это первичный ключ отношения (PRIMARY KEY), который однозначно определяет кортеж основного отношения. В подчиненном отношении для моделирования связи должен присутствовать набор атрибутов, соответствующий первичному ключу основного отношения. Данный набор атрибутов в подчиненном отношении принято называть внешним ключом (FOREIGN KEY).

Связи между отношениями
Любая таблица имеет один или несколько столбцов, значения которых однозначно идентифицируют каждую ее строку. Такой столбец (или совокупность столбцов) называется первичным ключом.
Взаимосвязи таблиц в реляционной модели поддерживаются внешними ключами. Внешний ключ – это столбец (или совокупность столбцов), значения которого однозначно характеризуют сущности, представленные строками некоторого другого отношения, т.е. задают значения их первичного ключа.

Реляционная алгебра – это набор операций, которые принимают отношения в качестве операндов и возвращают отношение в качестве результата.
Алгеброй называется множество объектов с заданной на нем совокупностью операции, замкнутых относительно этого множества, называемого основным множеством.
Основным множеством в реляционном алгебре является множество отношений.
Всего Коддом было предложено 8 операций.
В общем это множество избыточное, так как одни операции могут быть представлены через другие, однако множество операций выбрано из соображений максимального удобства при реализации произвольных запросов к БД.
Все множество операций можно разделить на две группы: теоретико-множественные операции и специальные операции.
В первую группу входят 4 операции. Три первые теоретико-множественные операции являются бинарными, то есть в них участвуют два отношения и они требуют эквивалентных схем исходных отношений.

Операции над отношениями
Объединение
Пересечение
Разность
Произведение
Выборка (ограничение)
Проекция
Соединение
Деление

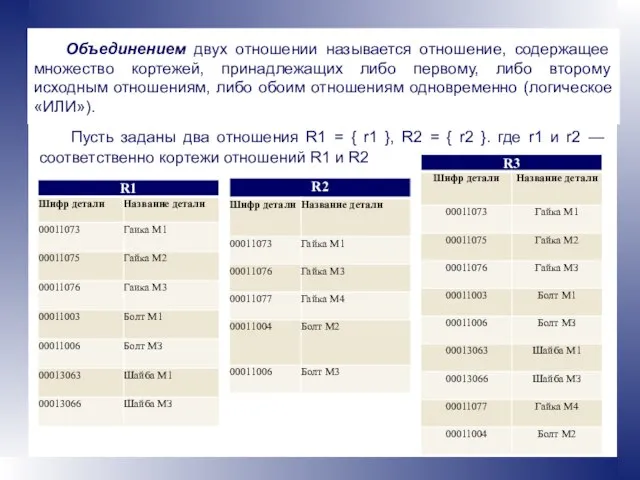
Объединением двух отношении называется отношение, содержащее множество кортежей, принадлежащих либо первому, либо второму исходным отношениям, либо обоим отношениям одновременно (логическое «ИЛИ»).
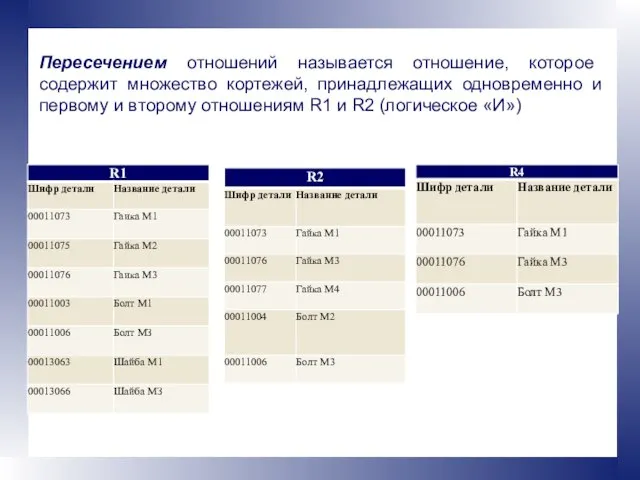
Пусть заданы два отношения R1 = { r1 }, R2 = { r2 }. где r1 и r2 — соответственно кортежи отношений R1 и R2

Пересечением отношений называется отношение, которое содержит множество кортежей, принадлежащих одновременно и первому и второму отношениям R1 и R2 (логическое «И»)

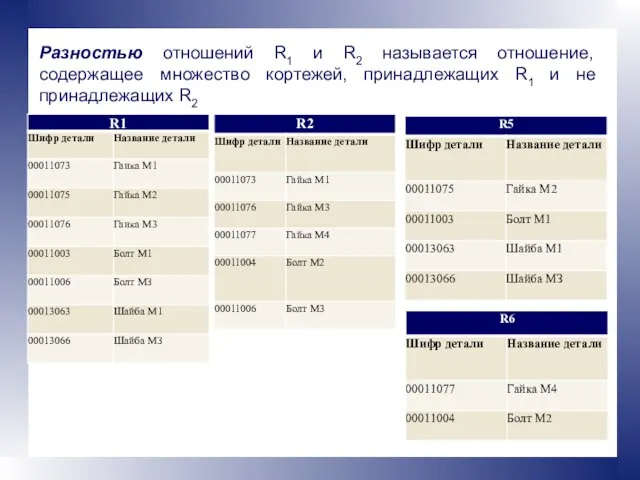
Разностью отношений R1 и R2 называется отношение, содержащее множество кортежей, принадлежащих R1 и не принадлежащих R2

Пример
Исходными являются три отношения R1 R2 и R3.
Все они имеют эквивалентные схемы.
R1= (ФИО, Паспорт, Школа);
R2= (ФИО, Паспорт, Школа);
R3= (ФИО, Паспорт, Школа).
Рассмотрим ситуацию поступления в высшие учебные заведения, которая была характерна для периода, когда были разрешены так называемые репетиционные вступительные экзамены, которые сдавались раньше основных вступительных экзаменов в вуз.
Отношение R1 содержит список абитуриентов, сдававших репетиционные экзамены.
Отношение, R2 содержит список абитуриентов, сдававших экзамены на общих условиях.
Отношение R3 содержит список абитуриентов, принятых в институт. Будем считать, что при неудачной сдаче репетиционных экзаменов абитуриент мог делать вторую попытку и сдавать экзамены в общем потоке.

Ответим на следующие вопросы:
Полный список всех поступавших в вузы.
Список абитуриентов поступивших по репетиционному тестированию.
Список абитуриентов, которые поступали два раза и не поступили в вуз.
Список абитуриентов, которые поступили в вуз с первого раза, то есть они сдавали экзамены только один раз и сдали их так хорошо, что сразу были зачислены в вуз.
Список абитуриентов, которые поступили в вуз только со второго раза.
Список абитуриентов, которые поступали только один раз и не поступили.

Результатом произведения двух отношений является отношение, содержащее все возможные кортежи, которые являются сцеплением двух кортежей, принадлежащих двум отношениям.
Эта операция не накладывает никаких дополнительных условий на схемы исходных отношений, поэтому операция расширенного декартова произведения, обозначаемая R1 ® R2, допустима для любых двух отношений.
Сцеплением, или конкатенацией, кортежей с =
и q =
называется кортеж, полученный добавлением значений второго в конец первого.
Сцепление кортежей с и q обозначается как (с , q).
(с, q) = <с1 с2, ... , сn, q1, q2, .... qm>
Здесь n — число элементов в первом кортеже с, m — число элементов во втором кортеже q.

Расширенным декартовым произведением отношения R, степени n со схемой
SR1=(А1,А2...,Аn)
и отношения R2 степени m со схемой
SR2=(В1,В2, ... , Вm)
называется отношение R3 степени n+m со схемой
SR3 = (А1, А2, ... , Аn, В1, В2, ..., Вm),
содержащее кортежи, полученные сцеплением каждого кортежа r отношения R1 с каждым кортежем q отношения R2.
То есть если R1 = { r }, R2 = { q }
R1 ® R2 = {(r, q) | r e R1 ^ q e R2}

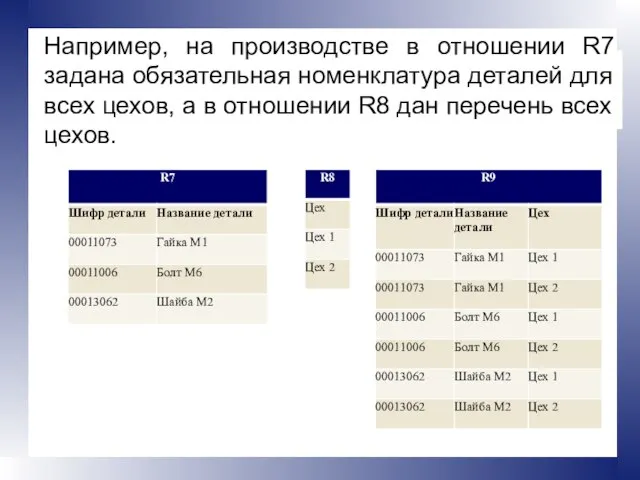
Например, на производстве в отношении R7 задана обязательная номенклатура деталей для всех цехов, а в отношении R8 дан перечень всех цехов.

Специальные операции реляционной алгебры
Первой специальной операцией реляционной алгебры является горизонтальный выбор, или операция фильтрации, или операция ограничения отношений.
Результатом выборки является отношение, содержащее все кортежи из исходного отношения, которые удовлетворяют определённому условию.

Пусть а — булевское выражение, составленное из термов сравнения с помощью связок И , ИЛИ , НЕ и, возможно, скобок. В качестве термов сравнения допускаются:
а) терм А ос а, где А — имя некоторого атрибута, принимающего значения из домена D; а — константа, взятая из того же домена D; ос — одна из допустимых для данного домена D операций сравнения;
б) терм А ос В, где А, В — имена некоторых Q-сравнимых атрибутов, то есть атрибутов, принимающих значения из одного и то же домена D.
Тогда результатом операции выбора, или фильтрации, заданной на отношении R в виде булевского выражения, определенного на атрибутах отношения R, называется отношение, включающее те кортежи из исходного отношения, для которых истинно условие выбора или фильтрации

Например, выбрать из R9 детали с шифром «0011073». R12 =R9[ Шифр детали = «0011003»]

Проекцией отношения R на набор атрибутов В, обозначаемой R[B], называется отношение со схемой, соответствующей набору атрибутов В, содержащему кортежи, получаемые из кортежей исходного отношения R путем удаления из них значений, не принадлежащих атрибутам из набора В.
По определению отношений все дублирующие кортежи удаляются из результирующего отношения.
Результатом проекции является отношение, содержащее все кортежи после удаления из них некоторых атрибутов.
возможно указание всех атрибутов исходного отношения для проекции – получится тождественная проекция;
возможно указать пустой список атрибутов – получится нулевая проекция.

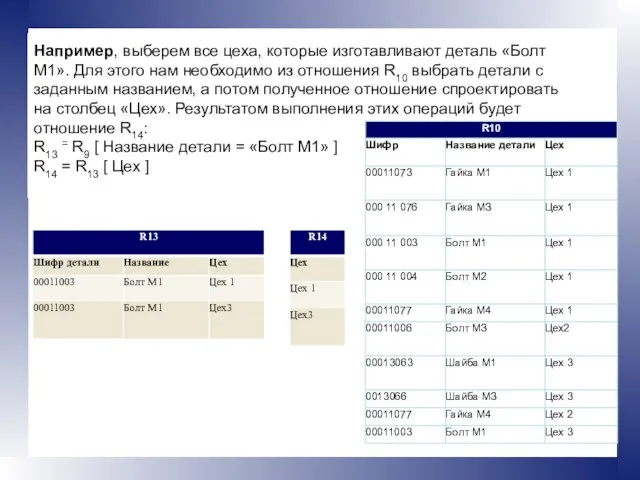
Например, выберем все цеха, которые изготавливают деталь «Болт M1». Для этого нам необходимо из отношения R10 выбрать детали с заданным названием, а потом полученное отношение спроектировать на столбец «Цех». Результатом выполнения этих операций будет отношение R14:
R13 = R9 [ Название детали = «Болт M1» ]
R14 = R13 [ Цех ]

Операция условного соединения.
Результат соединения – это отношение, кортежи которого являются сочетанием двух кортежей, принадлежащих двум начальным отношениям и имеющих общие значения для одного или нескольких атрибутов (общее значение в результирующем отношении появляется только один раз).
Пусть R = {r}, Q = { q } — исходные отношения,
SR, SQ — схемы отношений R и Q соответственно.
SR = (А1, А2, ... , Ak): SQ = (В1 В2, ... , Bm),
где А, В, — имена атрибутов в схемах отношений R и Q соответственно. При этом полагаем, что заданы наборы атрибутов А и В и эти наборы состоят из Q-сравнимых атрибутов.
Тогда соединением отношений R и Q при условии р будет подмножество декартова произведения отношений R и Q, кортежи которого удовлетворяют условию р

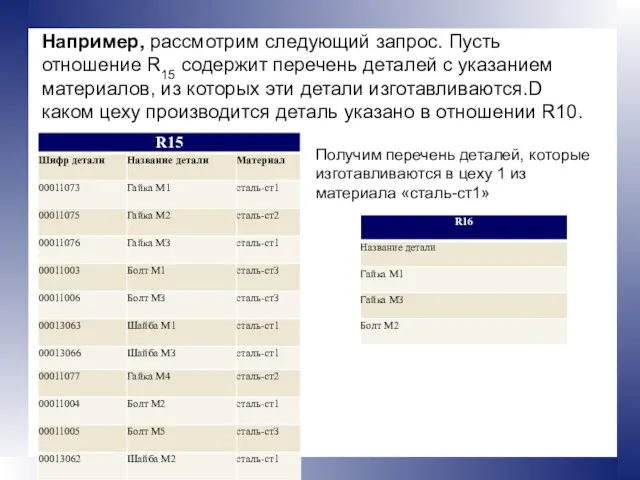
Например, рассмотрим следующий запрос. Пусть отношение R15 содержит перечень деталей с указанием материалов, из которых эти детали изготавливаются.D каком цеху производится деталь указано в отношении R10.
Получим перечень деталей, которые изготавливаются в цеху 1 из материала «сталь-ст1»

Операция деления . Результатом деления двух отношений (бинарного и унарного) является отношение, содержащее все значения атрибута первого бинарного отношения, которые соответствуют всем значениям унарного отношения.

Пусть заданы два отношения:
A с заголовком {a1, a2, ..., an, b1, b2, ..., bm}
B с заголовком {b1, b2, ..., bm}.
Будем считать, что атрибут bi отношения A и атрибут bi отношения B не только обладают одним и тем же именем, но и определены на одном и том же домене.
Назовем множество атрибутов {aj} составным атрибутом a, а множество атрибутов {bj} - составным атрибутом b.
После этого будем говорить о реляционном делении бинарного отношения A(a,b) на унарное отношение B(b).
Результатом деления A на B является унарное отношение C(a), состоящее из кортежей v таких, что в отношении A имеются кортежи
такие, что множество значений {w} включает все множество значений атрибута b в отношении B.