Содержание
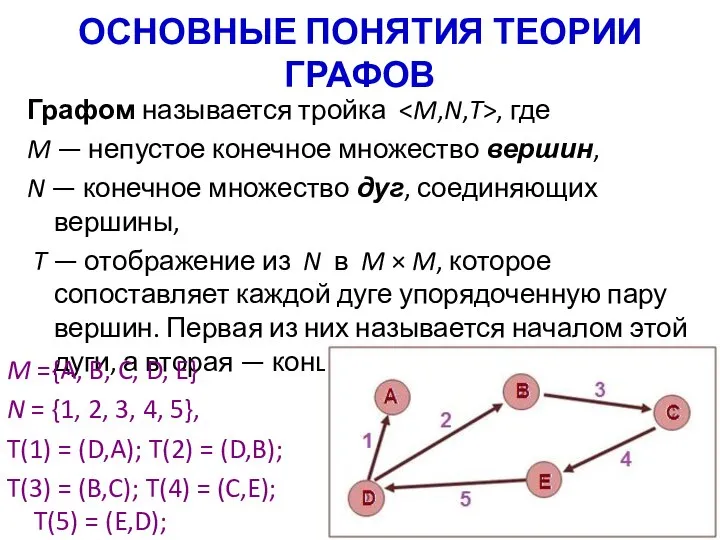
- 2. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ГРАФОВ Графом называется тройка , где M — непустое конечное множество вершин, N
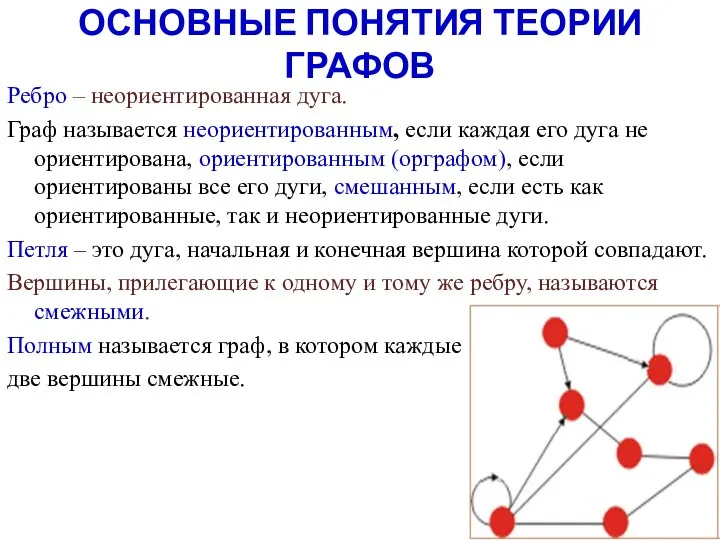
- 3. Ребро – неориентированная дуга. Граф называется неориентированным, если каждая его дуга не ориентирована, ориентированным (орграфом), если
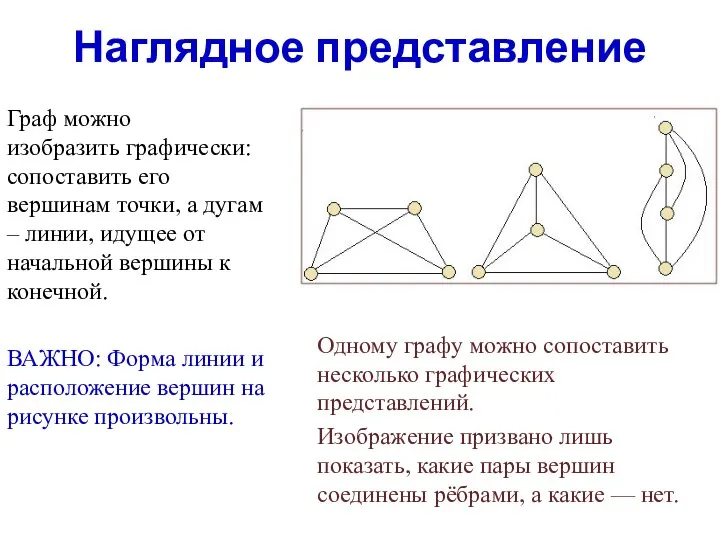
- 4. Наглядное представление Одному графу можно сопоставить несколько графических представлений. Изображение призвано лишь показать, какие пары вершин
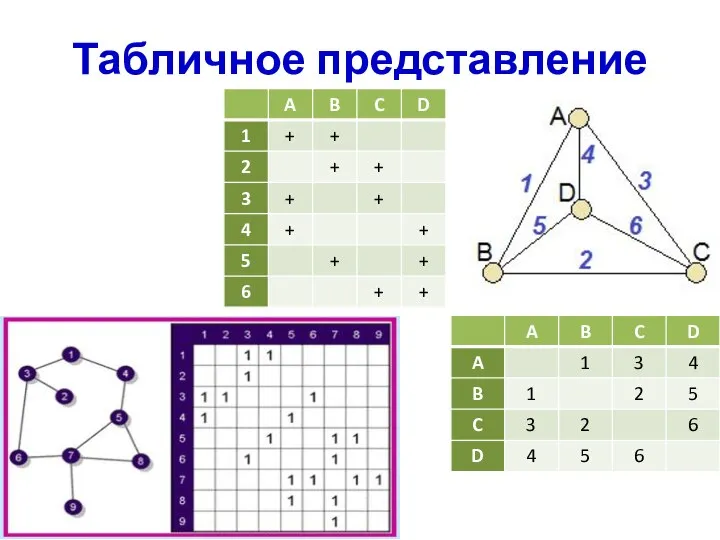
- 5. Табличное представление
- 6. СВЯЗНОСТЬ ГРАФА Маршрутом называется такая конечная или бесконечная последовательность ребер, что каждые два соседних ребра имеют
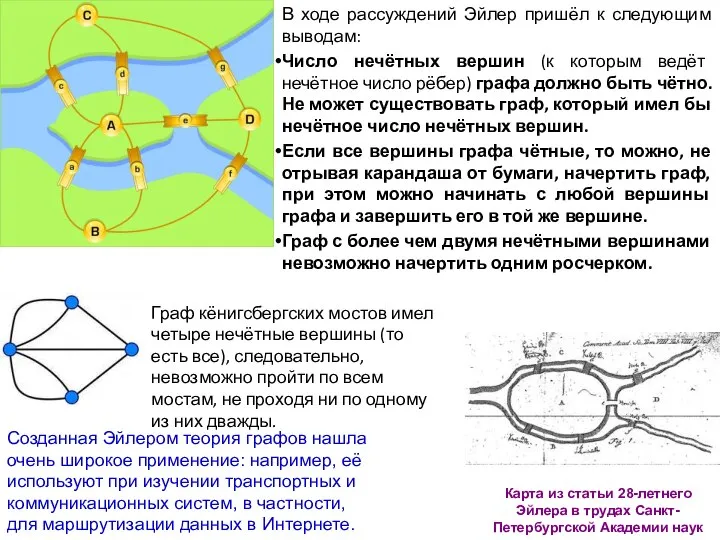
- 7. Цикл Эйлера Среди таких задач наибольшей известностью пользуется задача о семи кёнигсбергских мостах: в городе Кёнигсберге
- 8. В ходе рассуждений Эйлер пришёл к следующим выводам: Число нечётных вершин (к которым ведёт нечётное число
- 9. Гамильтонов цикл Гамильтонов путь — маршрут, содержащий каждую вершину графа ровно один раз. Гамильтонов путь, начальная
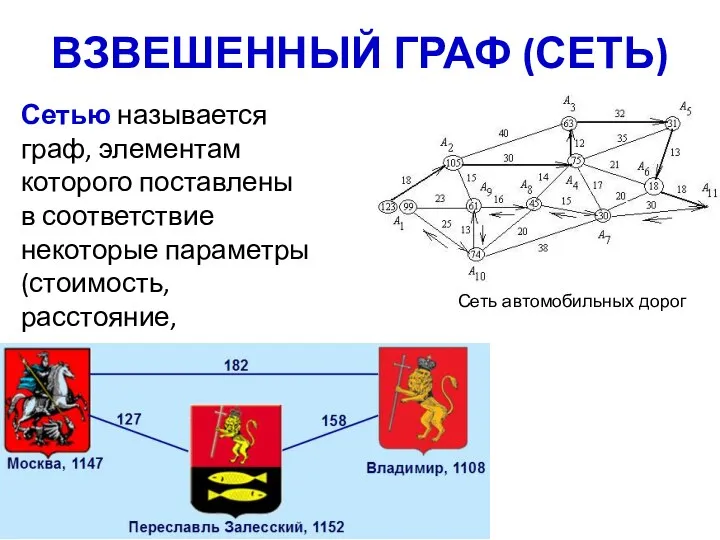
- 10. ВЗВЕШЕННЫЙ ГРАФ (СЕТЬ) Сетью называется граф, элементам которого поставлены в соответствие некоторые параметры (стоимость, расстояние, пропускная
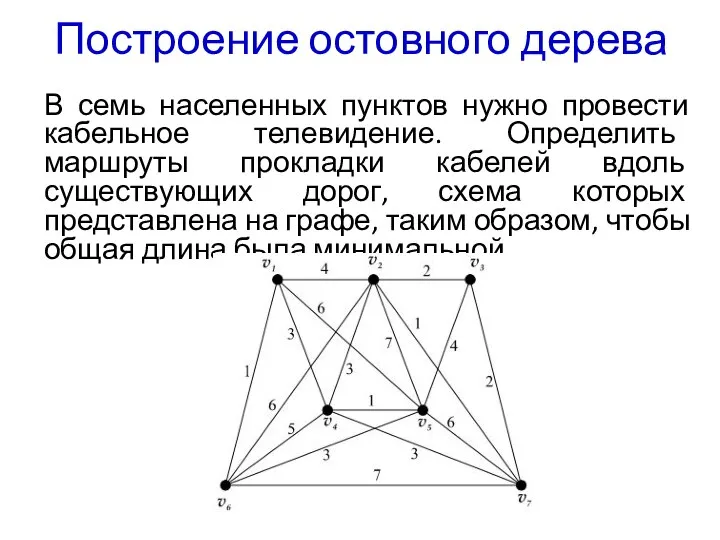
- 11. Построение остовного дерева В семь населенных пунктов нужно провести кабельное телевидение. Определить маршруты прокладки кабелей вдоль
- 12. Математическая постановка Предположим, что задан связный граф , и каждой его дуге j∈N сопоставлено некоторое число
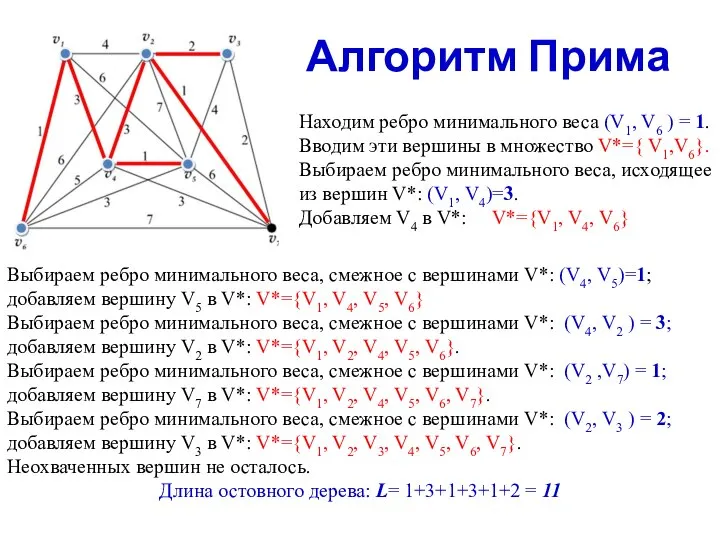
- 13. Алгоритм Прима —алгоритм построения минимального остовного дерева взвешенного связного неориентированного графа. Алгоритм впервые был открыт в
- 14. Алгоритм Прима Находим ребро минимального веса (V1, V6 ) = 1. Вводим эти вершины в множество
- 15. Алгоритм Краскала Алгоритм, более привлекательный в вычислительном отношении, был предложен Джозефом Краскалом в 1957 г. Алгоритм
- 16. Алгоритм Краскала Находим ребро минимального веса 1: (V1, V6 ) = 1. Вводим вершины в множество
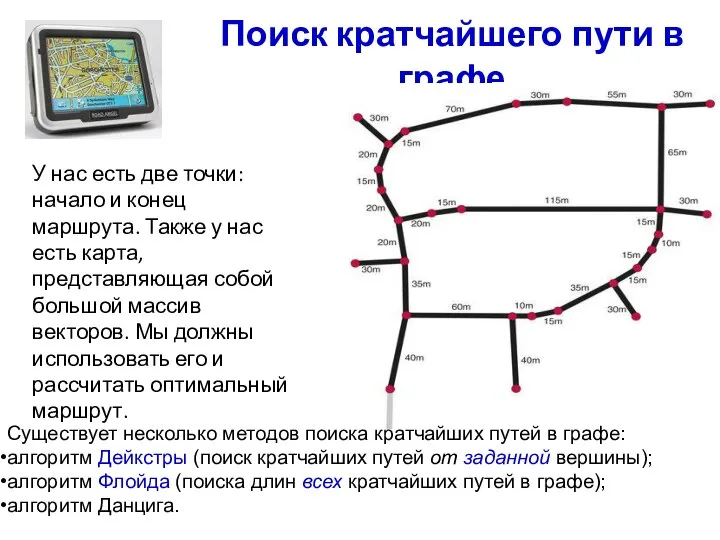
- 17. Поиск кратчайшего пути в графе У нас есть две точки: начало и конец маршрута. Также у
- 18. Алгоритм Дейкстры Метод считается одним из наиболее эффективных алгоритмов решения задачи. Предложен в 1959 г. голландским
- 19. Идея алгоритма Дейкстры Окрасим вершину S и m ближайших к ней вершин. Построим для каждой неокрашенной
- 20. Алгоритм Дейкстры Каждой вершине X в ходе алгоритма присваивается число d(x), равное длине кратчайшего пути из
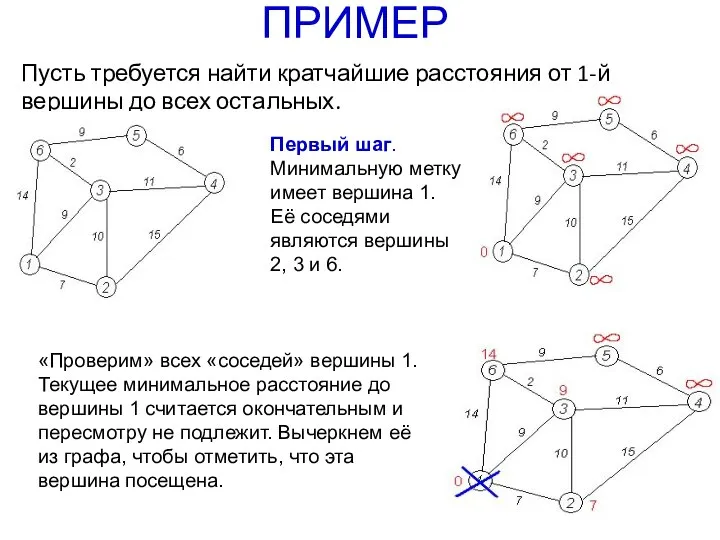
- 21. ПРИМЕР Пусть требуется найти кратчайшие расстояния от 1-й вершины до всех остальных. Первый шаг. Минимальную метку
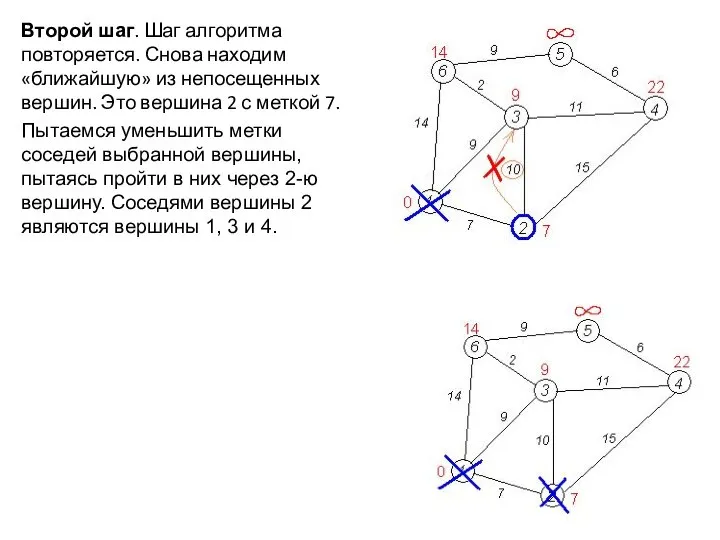
- 22. Второй шаг. Шаг алгоритма повторяется. Снова находим «ближайшую» из непосещенных вершин. Это вершина 2 с меткой
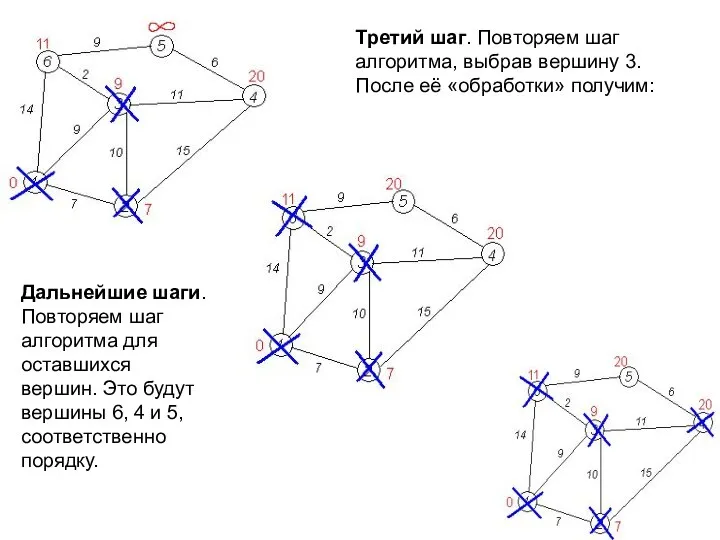
- 23. Третий шаг. Повторяем шаг алгоритма, выбрав вершину 3. После её «обработки» получим: Дальнейшие шаги. Повторяем шаг
- 24. Алгоритм Флойда - Уоршелла Разработан в 1962 году Робертом Флойдом и Стивеном Уоршеллом В отличии от
- 25. Обозначения Перенумеруем вершины графа целыми числами от 1 до N. Обозначим через di,jm длину кратчайшего пути
- 26. Обозначения Обозначим через Dm матрицу размера NxN, элемент (i,j) которой совпадает с di,jm. Если в исходном
- 27. Суть алгоритма Флойда заключается в проверке того, не окажется ли путь из вершины i в вершину
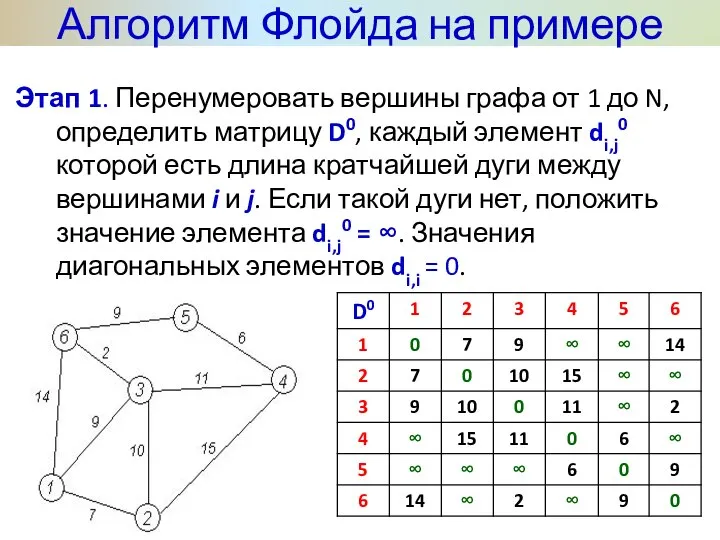
- 28. Этап 1. Перенумеровать вершины графа от 1 до N, определить матрицу D0, каждый элемент di,j0 которой
- 29. Матрицу S0, в которой будем запоминать последовательность вершин в кратчайшем пути, заполним так: sij = j
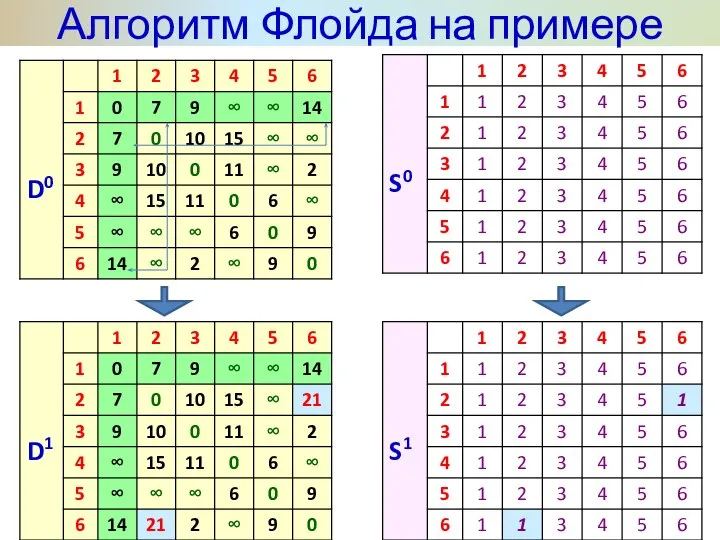
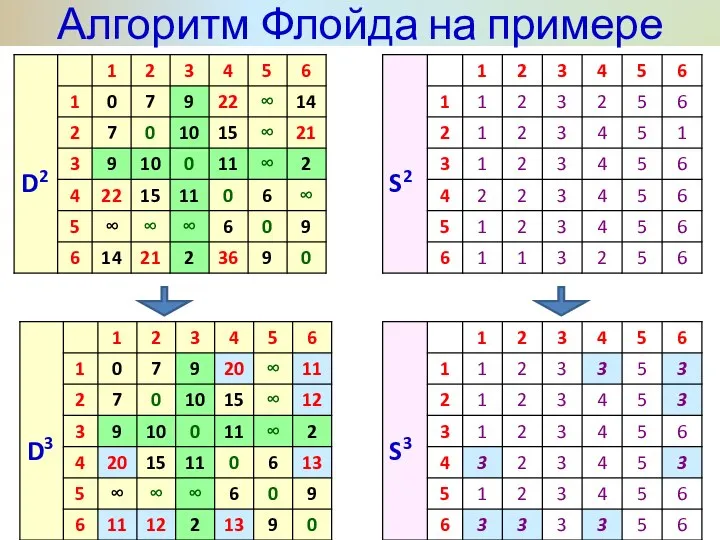
- 30. Алгоритм Флойда на примере Задаём строку m и столбец m как ведущую строку и ведущий столбец.
- 31. Алгоритм Флойда на примере
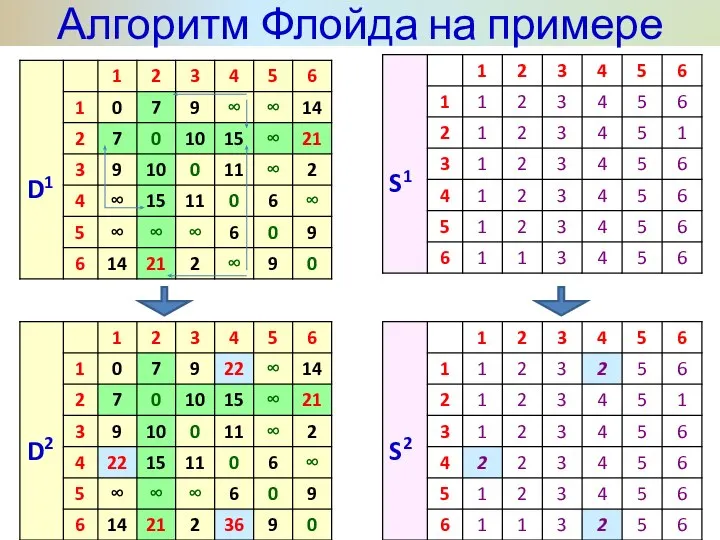
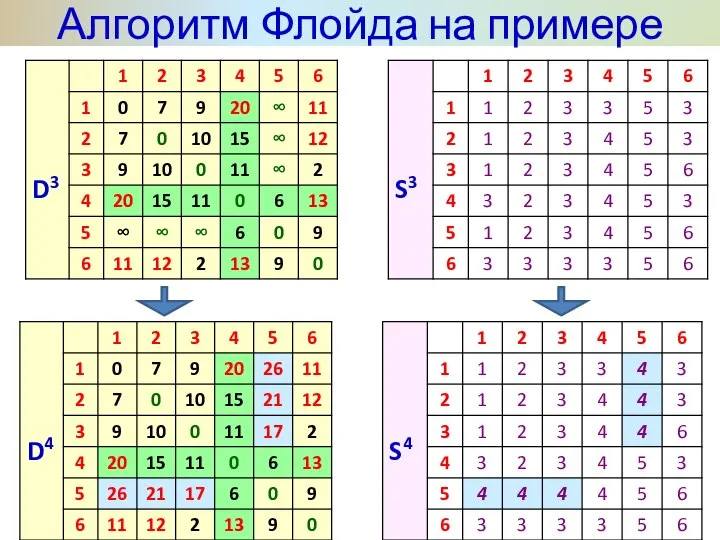
- 32. Алгоритм Флойда на примере
- 33. Алгоритм Флойда на примере
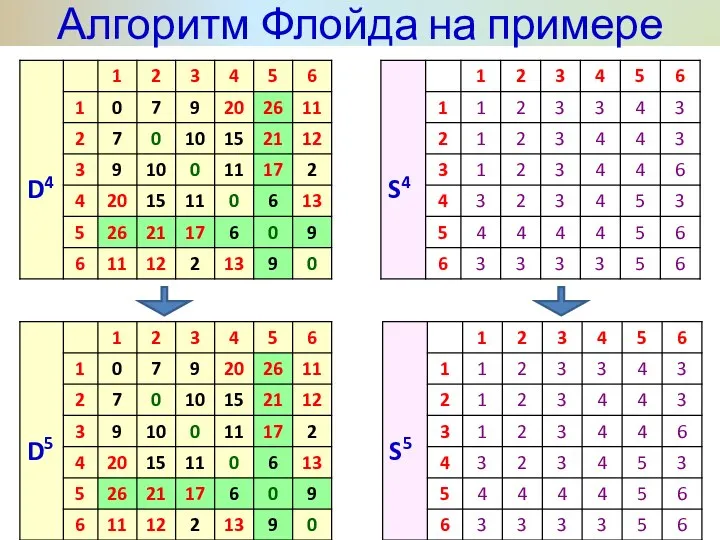
- 34. Алгоритм Флойда на примере
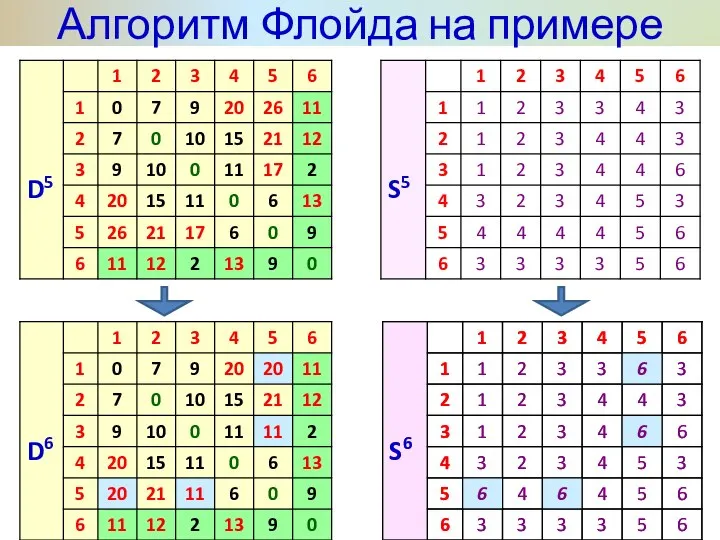
- 35. Алгоритм Флойда на примере
- 36. Алгоритм Флойда на примере
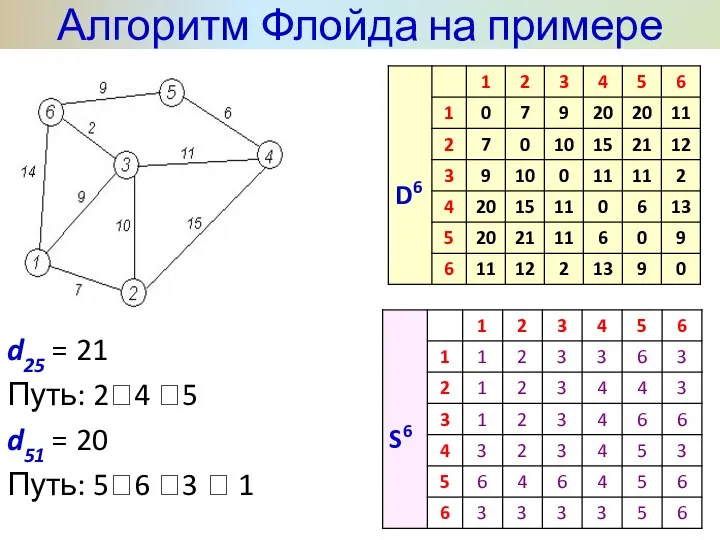
- 37. Алгоритм Флойда на примере Последний этап. После реализации N этапов алгоритма определение по матрицам Dn и
- 38. d25 = 21 Путь: 2?4 ?5 d51 = 20 Путь: 5?6 ?3 ? 1 Алгоритм Флойда
- 39. Задача коммивояжёра Формулировка (1934 г.) Коммивояжер должен выйти из первого города, посетить по разу в неизвестном
- 40. Идея метода состоит в следующем: чтобы избежать полного перебора нужно разделить огромное число перебираемых вариантов на
- 41. Применительно к задаче о коммивояжере идея метода ветвей и границ такова: Ветвление основано на следующем простом
- 42. В каждой строке матрицы стоимости найдем минимальный элемент и вычтем его из всех элементов строки. Сделаем
- 43. Удаляем k-тую строку и столбец l, поменяем на бесконечность значение элемента dlk (поскольку дуга (k,l) включена
- 44. В ходе решения ведется постоянный подсчет текущего значения нижней границы. Нижняя граница равна сумме всех вычтенных
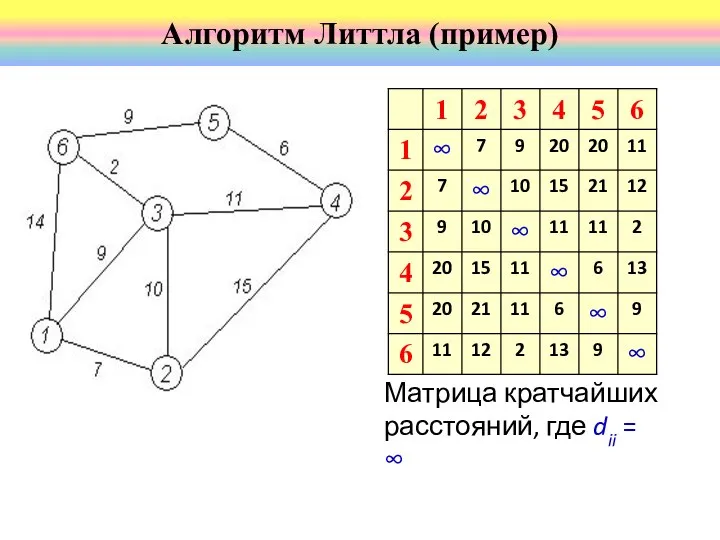
- 45. Матрица кратчайших расстояний, где dii = ∞ Алгоритм Литтла (пример)
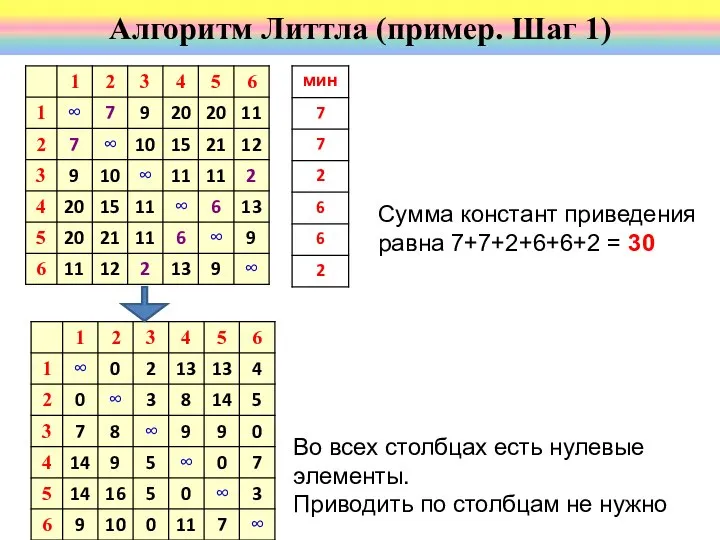
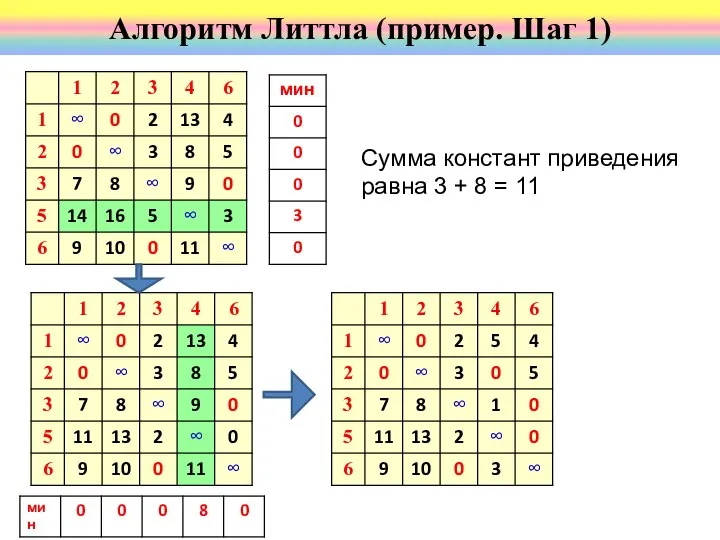
- 46. Алгоритм Литтла (пример. Шаг 1) Сумма констант приведения равна 7+7+2+6+6+2 = 30 Во всех столбцах есть
- 47. Тур, проходящий только через ребра нулевой стоимости, будет, очевидно, минимальным. Его стоимость 30. Алгоритм Литтла (пример.
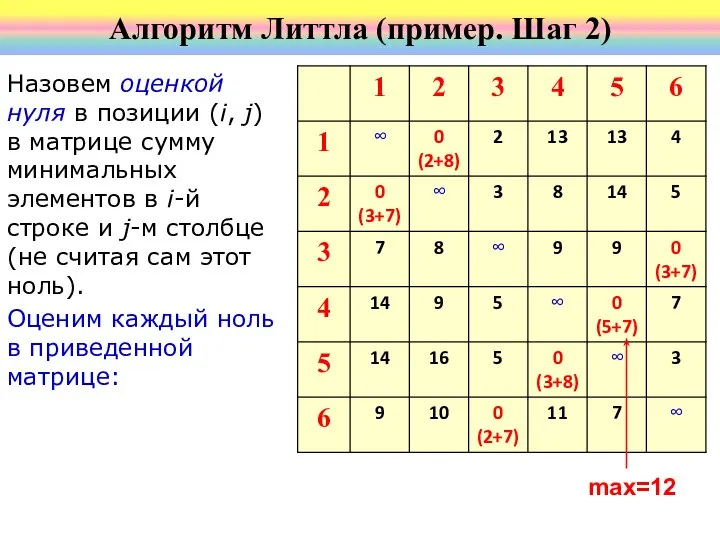
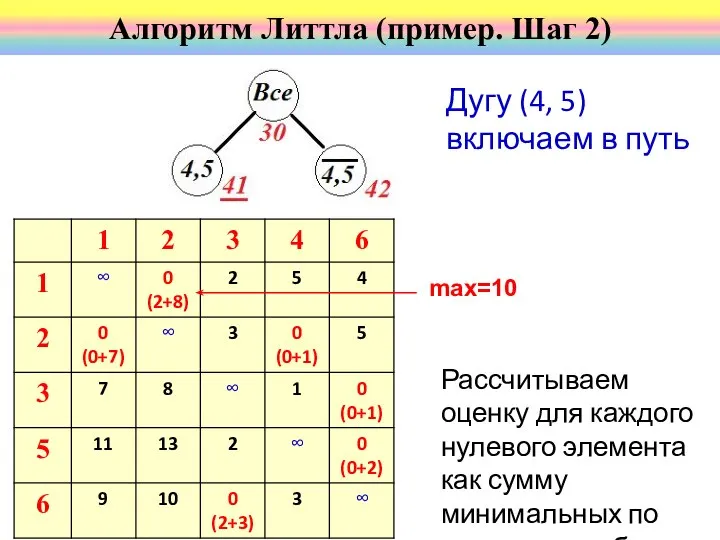
- 48. Алгоритм Литтла (пример. Шаг 2) Назовем оценкой нуля в позиции (i, j) в матрице сумму минимальных
- 49. Оценка k нуля, в позиции (i, j) означает буквально следующее: если в тур не будет включен
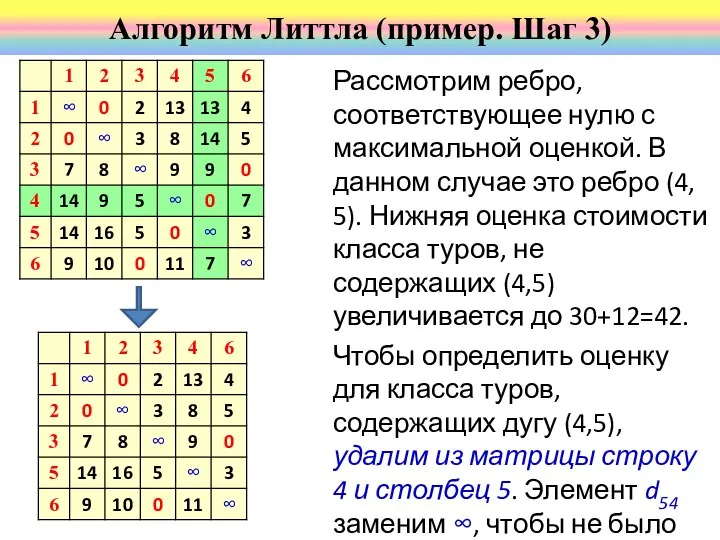
- 50. Рассмотрим ребро, соответствующее нулю с максимальной оценкой. В данном случае это ребро (4, 5). Нижняя оценка
- 51. Алгоритм Литтла (пример. Шаг 1) Сумма констант приведения равна 3 + 8 = 11
- 52. Рассчитываем оценку для каждого нулевого элемента как сумму минимальных по строке и столбцу Алгоритм Литтла (пример.
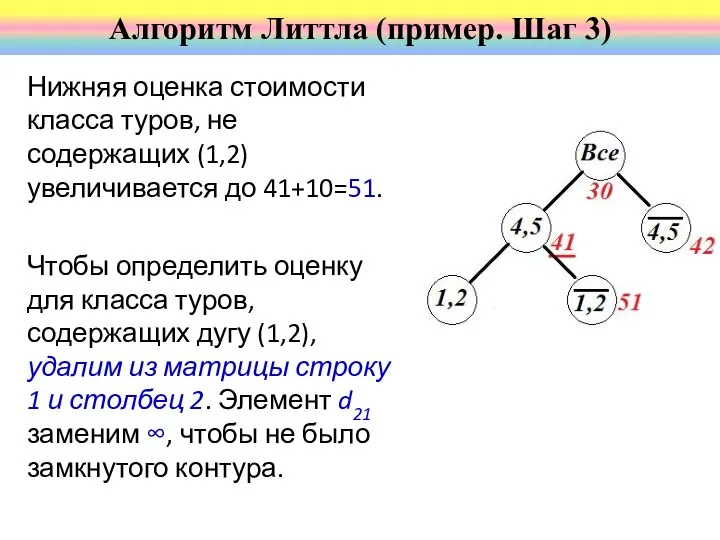
- 53. Нижняя оценка стоимости класса туров, не содержащих (1,2) увеличивается до 41+10=51. Чтобы определить оценку для класса
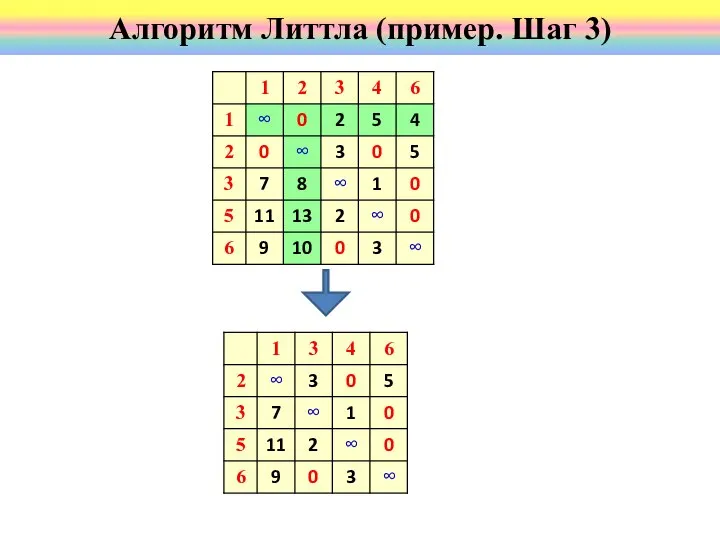
- 54. Алгоритм Литтла (пример. Шаг 3)
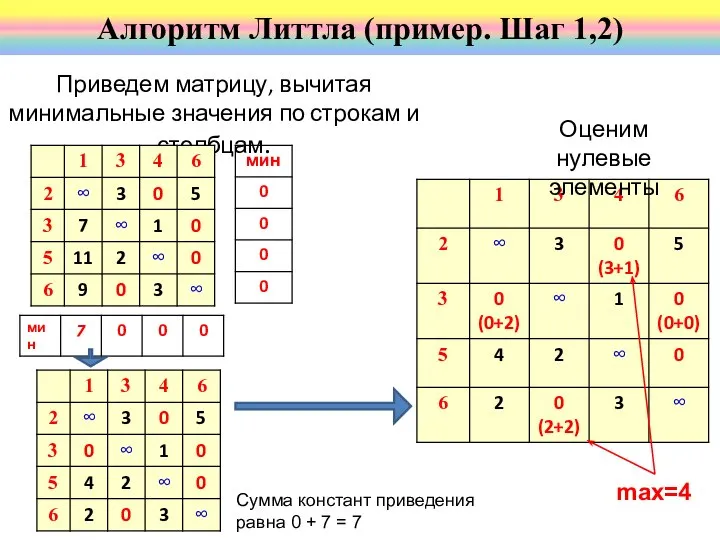
- 55. Приведем матрицу, вычитая минимальные значения по строкам и столбцам. Алгоритм Литтла (пример. Шаг 1,2) Сумма констант
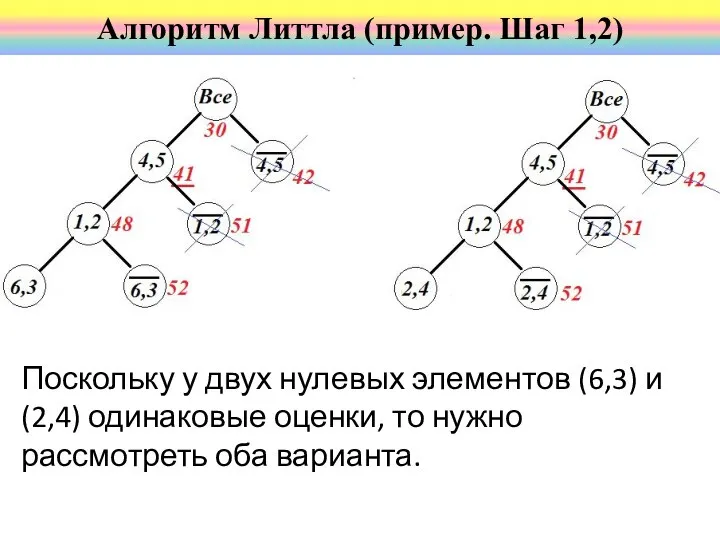
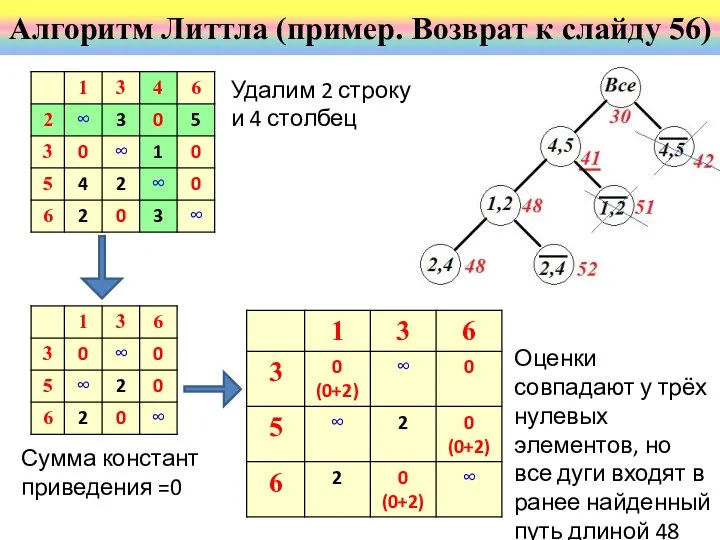
- 56. Поскольку у двух нулевых элементов (6,3) и (2,4) одинаковые оценки, то нужно рассмотреть оба варианта. Алгоритм
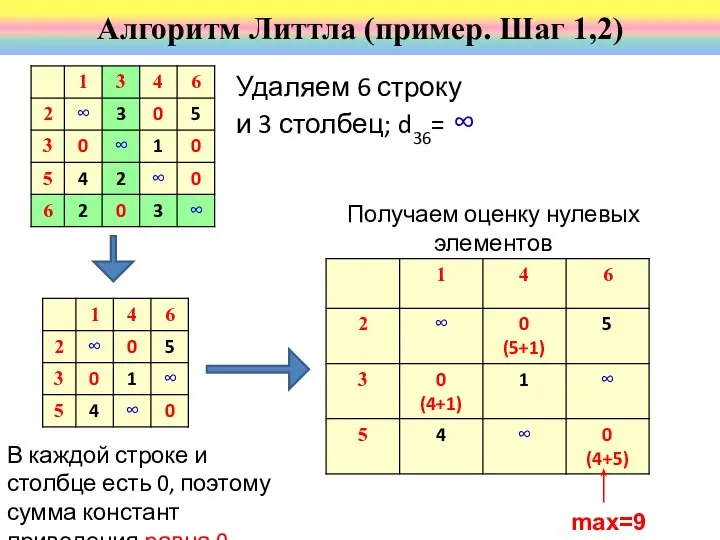
- 57. Получаем оценку нулевых элементов Алгоритм Литтла (пример. Шаг 1,2) Удаляем 6 строку и 3 столбец; d36=
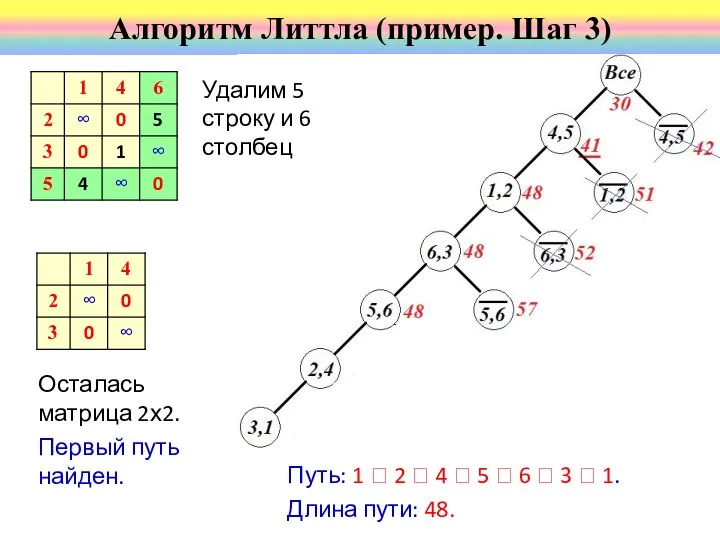
- 58. Осталась матрица 2х2. Первый путь найден. Алгоритм Литтла (пример. Шаг 3) Удалим 5 строку и 6
- 59. Оценки совпадают у трёх нулевых элементов, но все дуги входят в ранее найденный путь длиной 48
- 61. Скачать презентацию













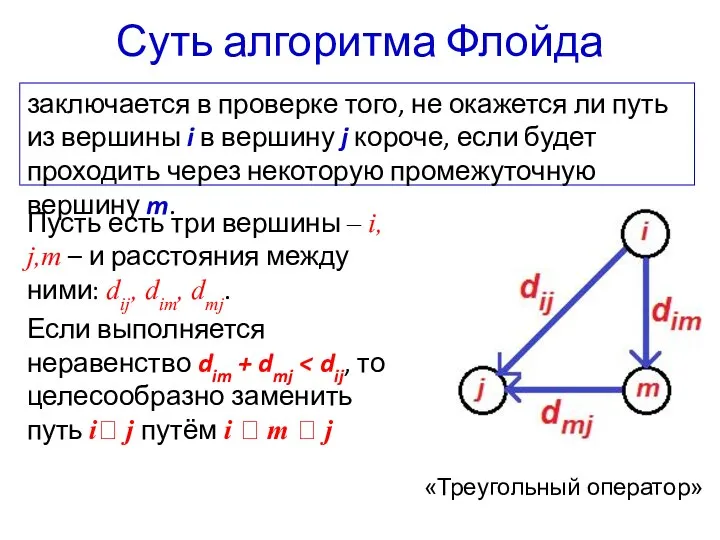











 Мастер украшения помогает сделать праздник
Мастер украшения помогает сделать праздник Отчет о научно-организационной деятельности Президиума АН РБ в 2009 году
Отчет о научно-организационной деятельности Президиума АН РБ в 2009 году Глянец в дизайне. Фотоальбом
Глянец в дизайне. Фотоальбом Проблема адекватности восприятия текста
Проблема адекватности восприятия текста Презентация на тему Оборона Сталинграда
Презентация на тему Оборона Сталинграда  Красная книга России (4 класс)
Красная книга России (4 класс) Введение в техническую графику. Тест
Введение в техническую графику. Тест Этапы проектной деятельности
Этапы проектной деятельности Особенности питания детей грудного возраста
Особенности питания детей грудного возраста До свидания! До новых встреч!
До свидания! До новых встреч! Устройство компьютера
Устройство компьютера Автомат световых эффектов. Схема
Автомат световых эффектов. Схема Изменяющаяся роль медицинских представителей и фармацевтов в аптеках Евгения Домнина Руководитель проектов Москва. 7 декабря 2
Изменяющаяся роль медицинских представителей и фармацевтов в аптеках Евгения Домнина Руководитель проектов Москва. 7 декабря 2 I возрастная ступень комплекса ГТО (от 6 до 8 лет)
I возрастная ступень комплекса ГТО (от 6 до 8 лет) Сказка в картинках - презентация
Сказка в картинках - презентация Презентация на тему Применение солей
Презентация на тему Применение солей Иконопись на Смоленщине
Иконопись на Смоленщине Создание портфолио
Создание портфолио Демократическое правовое государство
Демократическое правовое государство Информационная безопасность в юриспруденции. Лекция №2
Информационная безопасность в юриспруденции. Лекция №2 Роль стандартизации в инновационной сфере
Роль стандартизации в инновационной сфере Дестабилизирующие факторы современности
Дестабилизирующие факторы современности Презентация на тему Сахарный диабет
Презентация на тему Сахарный диабет Литвин, преза, готовая
Литвин, преза, готовая Деньги и инстинкты
Деньги и инстинкты Построение Сечения объемных фигур в Paint
Построение Сечения объемных фигур в Paint Город мечты
Город мечты Страхование строительно-монтажных рисков и послепусковых гарантийных обязательств
Страхование строительно-монтажных рисков и послепусковых гарантийных обязательств