Содержание
- 2. Литература
- 3. Литература Сайт кафедры инженерная графика: IGRAPH. SSAU.RU
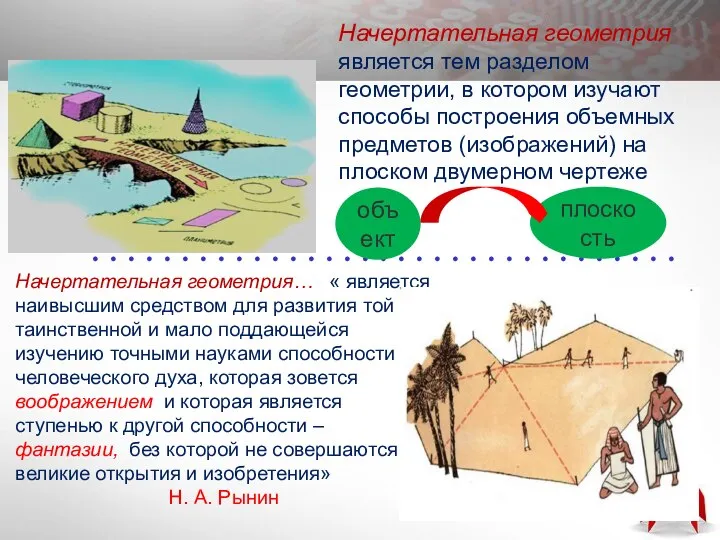
- 4. Начертательная геометрия является тем разделом геометрии, в котором изучают способы построения объемных предметов (изображений) на плоском
- 5. 1.2. Символика и обозначения.
- 6. ∊ - принадлежность ⊂ - лежит ≡ - совпадение ‖ - параллельность ∩ - пересечение ⊥
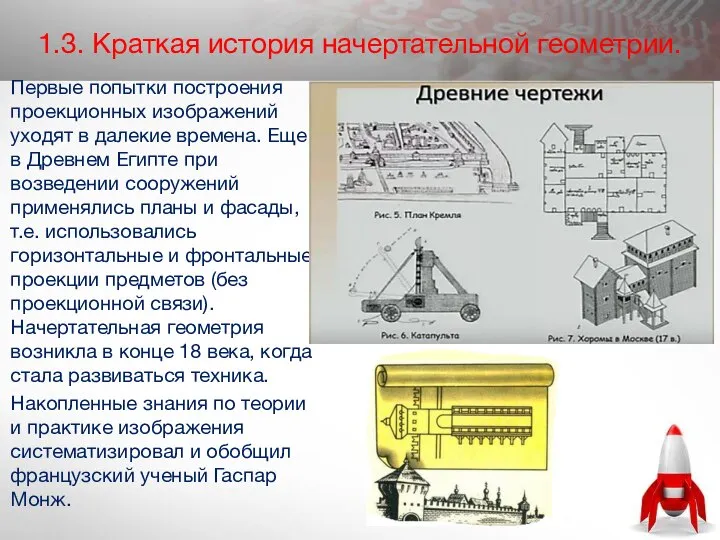
- 7. 1.3. Краткая история начертательной геометрии. Первые попытки построения проекционных изображений уходят в далекие времена. Еще в
- 8. Он впервые предложил рассматривать плоский чертеж из двух проекций как результат совмещения двух плоскостей проекций вращением
- 9. Работа Монжа «Начертательная геометрия» была опубликована в 1795г., как учебное пособие. В России курс начертательной геометрии
- 10. 1.4.ВИДЫ ПРОЕЦИРОВАНИЯ Основной метод НГ – метод проецирования. Для построения изображений на плоскости используют три способа
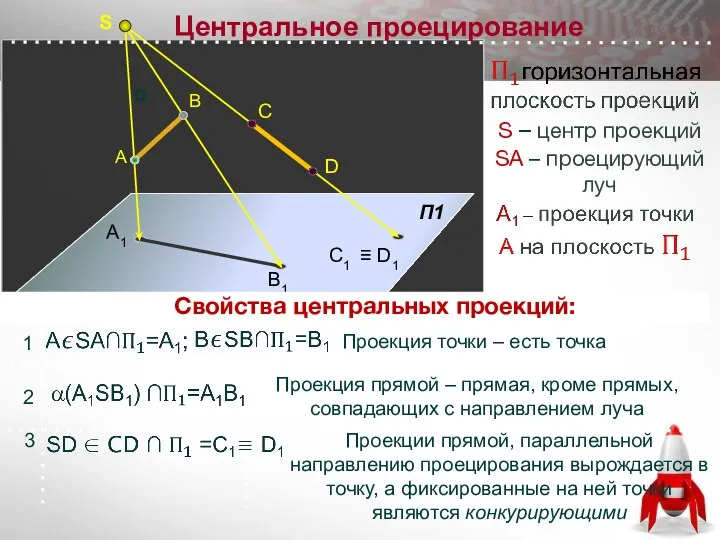
- 11. S А В A1 B1 C1 ≡ D1 D C Центральное проецирование Проекция прямой – прямая,
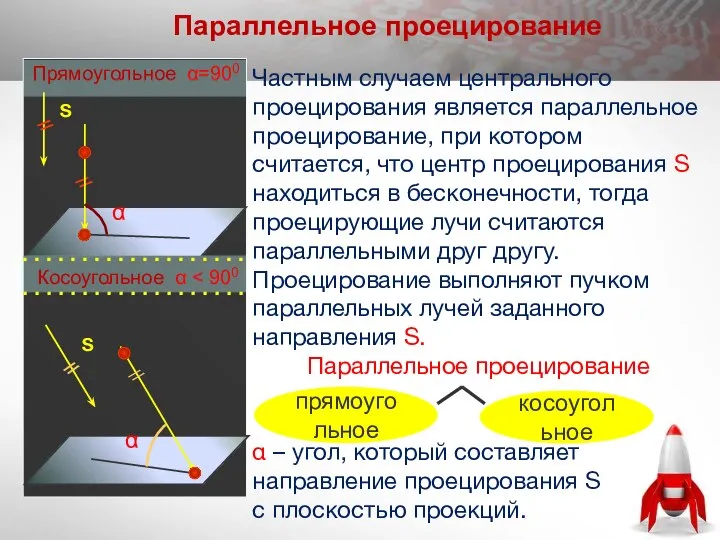
- 12. Частным случаем центрального проецирования является параллельное проецирование, при котором считается, что центр проецирования Ѕ находиться в
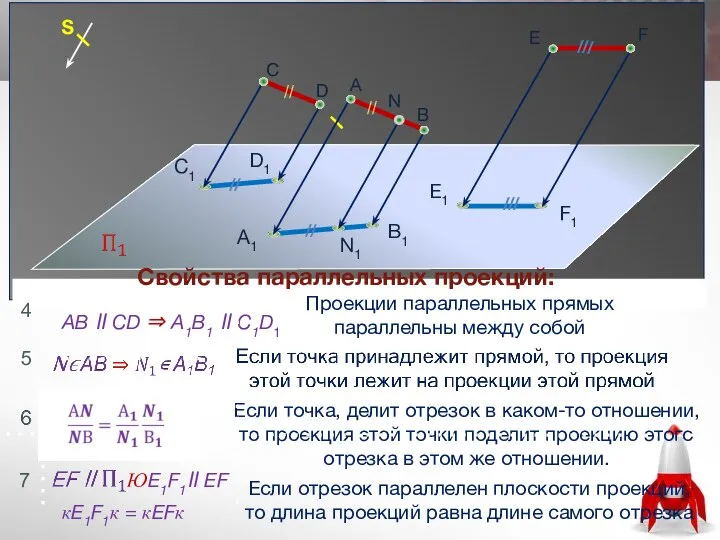
- 13. S С D A B N C1 D1 A1 N1 B1 AB ll CD ⇒ A1B1
- 14. 2.ОРТОГОНАЛЬНОЕ ПРОЕЦИРОВАНИЕ. Прямоугольное проецирование часто называют «ортогональным» ( от греч. «ortos» – прямой). 2.1.Проецирование точки. Комплексный
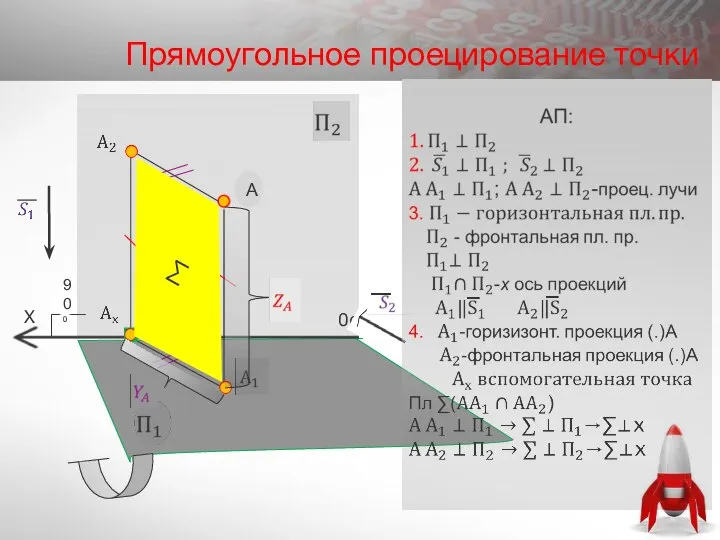
- 15. Прямоугольное проецирование точки A 90⁰ А 0 ∑ X 0
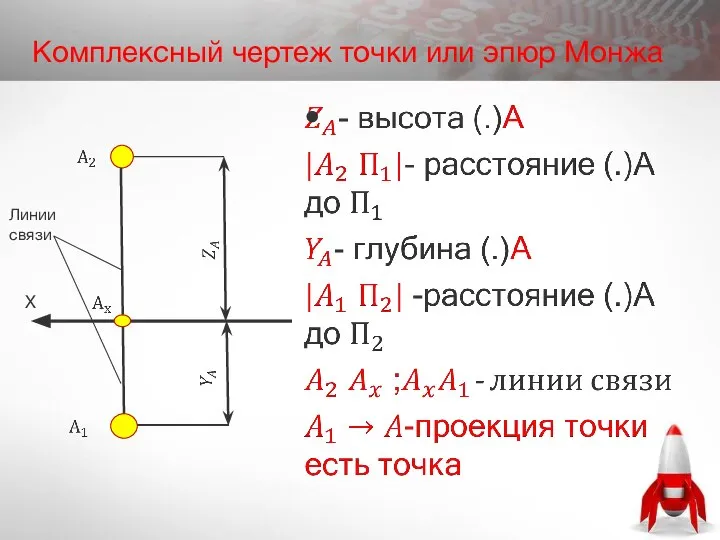
- 16. Х Линии связи Комплексный чертеж точки или эпюр Монжа
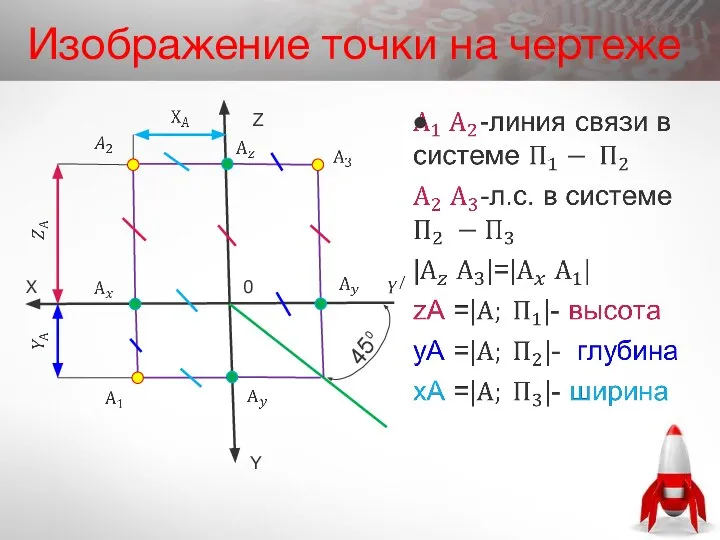
- 17. Свойства комплексного чертежа На комплексном чертеже находятся только проекции точки, самой точки нет. По двум проекциям
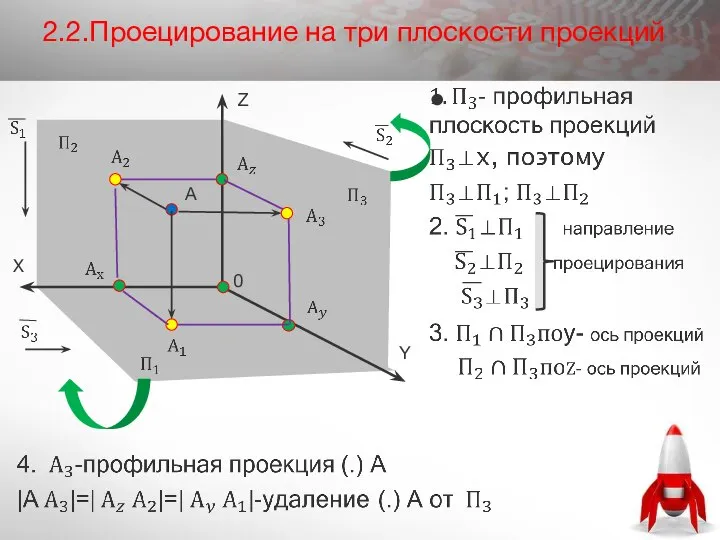
- 18. 2.2.Проецирование на три плоскости проекций А Z X Y 0
- 19. Изображение точки на чертеже Z X Y 0 45⁰
- 21. Скачать презентацию









 Н.А. Некрасов - поэт и публицист
Н.А. Некрасов - поэт и публицист Презентация на тему Соцветия
Презентация на тему Соцветия Разработка контрольно-измерительных материалов к дифференцированным зачётам
Разработка контрольно-измерительных материалов к дифференцированным зачётам Верещагин В.В. (1842-1904). Суриков В.И. Айвазовский И.К. Середина 19-го - начало 20 вв. Часть 14
Верещагин В.В. (1842-1904). Суриков В.И. Айвазовский И.К. Середина 19-го - начало 20 вв. Часть 14 Повесть «Белые ночи»
Повесть «Белые ночи» Педагог-психолог
Педагог-психолог Интегрированный урок живописи и музыки
Интегрированный урок живописи и музыки Как нарисовать лягушку
Как нарисовать лягушку Перспективы развития газовой промышленности на Востоке России
Перспективы развития газовой промышленности на Востоке России Организация и производственная деятельность арсеналов и баз
Организация и производственная деятельность арсеналов и баз Безопасность в сети Интернет
Безопасность в сети Интернет Спирты
Спирты Город Карабаш
Город Карабаш Презентация на тему Статическая и динамическая механика легких
Презентация на тему Статическая и динамическая механика легких  Коммуникации в социальных медиа как инструмент для привлечения частных пожертвований
Коммуникации в социальных медиа как инструмент для привлечения частных пожертвований Жизненный путь новомученицы Татианы Гримблит (1903-1937)
Жизненный путь новомученицы Татианы Гримблит (1903-1937) Финансы и кредит (литература)
Финансы и кредит (литература) Значение пищеварения. Строение и функции пищеварительной системы
Значение пищеварения. Строение и функции пищеварительной системы Пожарные Автоцистерны
Пожарные Автоцистерны Получение образования в местах лишения свободы
Получение образования в местах лишения свободы ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ МЕДИЦИНСКИЙ УНИВЕРСИТЕТ им. М.ГОРЬКОГОПРОЯВЛЕНИЕ ВИРУСНЫХ ИНФЕКЦИЙ В ПОЛОСТИ РТА
ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ МЕДИЦИНСКИЙ УНИВЕРСИТЕТ им. М.ГОРЬКОГОПРОЯВЛЕНИЕ ВИРУСНЫХ ИНФЕКЦИЙ В ПОЛОСТИ РТА Виды Белгорода история и современность
Виды Белгорода история и современность ХИМИЧЕСКАЯ ПРОДУКЦИЯ
ХИМИЧЕСКАЯ ПРОДУКЦИЯ Комплексное исследование и сегментация рынка в системе маркетинга
Комплексное исследование и сегментация рынка в системе маркетинга Ландшафтоведение в поэзии, музыке, живописи и фото
Ландшафтоведение в поэзии, музыке, живописи и фото КОМА
КОМА 20140405_informatsionnye_sredstva_obucheniya
20140405_informatsionnye_sredstva_obucheniya Собирательные числительные
Собирательные числительные